Punkt-vor-Strich-Regel

Punkt- vor Strichrechnung ist eine Konvention in der Operatorrangfolge der Mathematik und besagt, dass Multiplikationen und Divisionen vor Additionen und Subtraktionen durchzuführen sind. Durch diese Konvention können in vielen Ausdrücken Klammern zu Gunsten der Lesbarkeit weggelassen werden. Zu weiteren Konventionen zum Fortlassen von Klammern siehe auch Operatorassoziativität.

Beispiel:

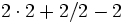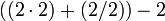
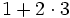• $2 \cdot 2 + 2 / 2 - 2$ Hier müssen zunächst die Multiplikation und die Division berechnet werden, wodurch sich ein Zwischenergebnis 4 + 1 − 2 ergibt. Das Ergebnis ist somit 3. Dies entspricht einer vollständigen Klammerung wie folgt: $((2 \cdot 2) + (2 / 2)) - 2$
• $1 + 2 \cdot 3$ Hier muss zunächst die Multiplikation berechnet werden, die das Zwischenergebnis 1 + 6 ergibt; das Endergebnis ist somit 7. Mit Klammern wäre hier 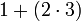$1 + (2\cdot 3)$ zu schreiben.

Manche Taschenrechner haben diese Regel nicht implementiert und benutzen die polnische Notation und brauchen somit keine Operatorrangfolge.

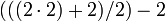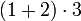Wieder andere führen jede Operation sukzessive durch. Als Ergebnisse werden bei obigen Beispielen dann 1 bzw. 9 ausgegeben, weil $(((2 \cdot 2) + 2) / 2) - 2$ bzw. $(1 + 2)\cdot 3$ gerechnet wird.