Pythagorasbaum

Pythagoras-Baum

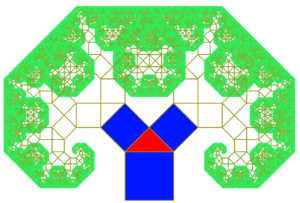
Ein Pythagoras-Baum ist eine besondere Art eines Fraktals. Das ursprüngliche Verfahren zum Erstellen eines Pythagoras-Baums basiert auf dem Satz des Pythagoras, in dem auf ein Quadrat zwei weitere, kleinere Quadrate im rechtem Winkel angeordnet werden. Durch rekursives Aufrufen dieser Konstruktionsvorschrift wird ein Fraktal erzeugt, das im Grenzfall der Form eines Baumes ähnelt. Durch den rechten Winkel des eingeschlossenen Dreiecks bleibt die Gesamtfläche jeder Ebene gleich, daher ist die Fläche des Grundelementes (Stammes) genau so groß wie die Summe der Fläche aller äußeren Elemente (Blätter).

Konstruktion

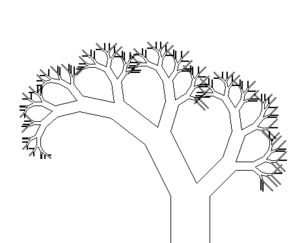
Aus einer Grundlinie wird ein Quadrat konstruiert. Auf diesem Grundelement (Stamm) wird auf der Oberseite ein Thaleskreis gezeichnet und dieser beliebig geteilt. Der entstehende Punkt wird mit dem Grundelement verbunden (Bild 1), so dass ein rechtwinkliges Dreieck entsteht. Aus den beiden entstandenen Schenkeln des Dreiecks wird wieder jeweils ein Quadrat konstruiert (Bild 2), ein Thaleskreis aufgezeichnet, dieser geteilt, ein rechtwinkliges Dreieck konstruiert (Bild 3) und so wieder zu einem Quadrat erweitert (Bild 4). Dieser Vorgang wird beliebig oft wiederholt.

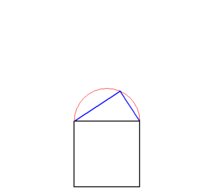
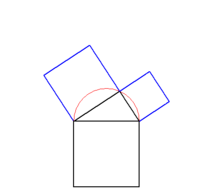
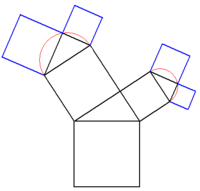
Bild 1	Bild 2	Bild 3	Bild 4

Weitere Formen

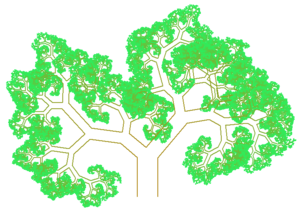
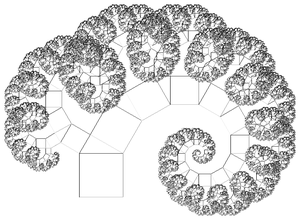
Da so ein Baum, der streng nach Pythagoras erzeugt wurde, sehr unnatürlich aussieht, kann natürlich auch von der Urform abgewichen werden.

Pythagoras-Baum	Fraktal-Baum
Rechtwinklige, gleichschenklige Dreiecke Verschiedene Farben	Freier Winkel Keine Quadrate
Pythagoras-Baum	Pythagoras-Baum
Rechtwinklige Dreiecke Verschiedene Farben	Keine rechtwinkligen Dreiecke Verschiedene Farben
Pythagoras-Baum	Pythagoras-Baum
Zufällige Stammlängen und zufällige Stammteilungsverhältnisse Rechtwinklige Dreiecke Verschiedene Farben	Gleichschenklige Dreiecke Rechtwinklige Dreiecke Verschiedene Farben
Pythagoras-Baum	SW Pythagoras-Baum

Weblinks

• Java-Applet
• Java-Applet
• Programmier-Beschreibung
• Besondere Pythagorasbäume