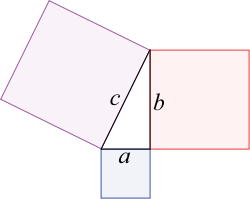
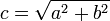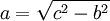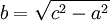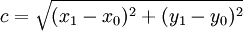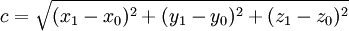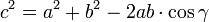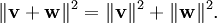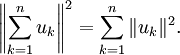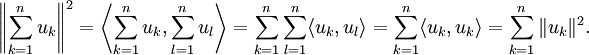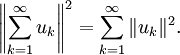Pythagoräisches Theorem

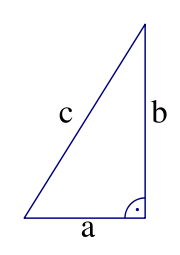
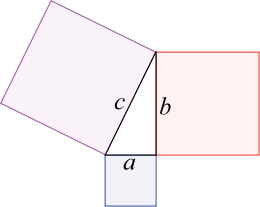
Der Satz des Pythagoras ist einer der fundamentalen Sätze der euklidischen Geometrie. Er besagt, dass in allen ebenen rechtwinkligen Dreiecken die Summe der Flächeninhalte der Kathetenquadrate gleich dem Flächeninhalt des Hypotenusenquadrates ist. Als Gleichung ausgedrückt lautet er

a² + b² = c²,

wobei a und b wie im Bild rechts für die Längen der am rechten Winkel anliegenden Seiten, der Katheten, stehen und c die Länge der dem rechten Winkel gegenüberliegenden Seite, der Hypotenuse, darstellt.

In der modernen Mathematik motiviert der Satz das Konzept des Senkrechtstehens in abstrakten Räumen.

Der Satz ist nach Pythagoras von Samos benannt, der als erster einen Beweis dafür gefunden haben soll, was allerdings in der Forschung stark bezweifelt wird. Schon lange vor Pythagoras war der „Satz des Pythagoras“ in Babylon und Indien bekannt, es gibt jedoch keinen Nachweis dafür, dass man dort bereits einen mathematischen Beweis hatte.

Mathematische Aussage und Anwendungen

Aussage

Sind a, b, c die Längen der Seiten eines rechtwinkligen Dreiecks mit c als Länge der Hypotenuse, so gilt:

a² + b² = c².

In Worten: Die Summe der Quadrate über den Katheten ist gleich dem Quadrat über der Hypotenuse.

Die Umkehrung gilt ebenso:

Gilt die Gleichung a² + b² = c² in einem Dreieck, so ist dieses Dreieck rechtwinklig, wobei der rechte Winkel der Seite c gegenüber liegt.

Eng verwandt mit dem Satz des Pythagoras sind der Höhensatz und der Kathetensatz. Diese beiden Sätze zusammen bilden zusammen mit dem Satz des Pythagoras die Satzgruppe des Pythagoras. Der unten beschriebene Kosinussatz ist eine Verallgemeinerung des pythagoreischen Satzes.

Anwendung

Aus dem Satz des Pythagoras folgt: Die Länge der Hypotenuse ist gleich der Quadratwurzel aus der Summe der Kathetenquadrate, es gilt also:

$c = \sqrt{a^2 + b^2}$

Die einfachste und wichtigste Anwendung des Satzes ist, aus zwei bekannten Seiten eines rechtwinkligen Dreiecks die Dritte zu berechnen. Dies ist durch Umformung der Gleichung für alle Seiten möglich:

$a = \sqrt{c^2 - b^2}$

$b = \sqrt{c^2 - a^2}$

Die Umkehrung des Satzes kann dazu verwendet werden, um zu überprüfen, ob ein gegebenes Dreieck rechtwinklig ist. Dazu wird schlicht getestet, ob die Gleichung des Satzes für die Seiten bei dem gegebenen Dreieck zutrifft. Es reicht also allein die Kenntnis der Seitenlängen eines gegebenen Dreiecks, um daraus zu schließen, ob es rechtwinklig ist:

Seitenlängen 3, 4, 5 => 3² + 4² = 9 + 16 = 25 = 5² => Das Dreieck ist rechtwinklig.

Seitenlängen 4, 5, 6 => 4² + 5² = 16 + 25 = 41 ≠ 6² => Das Dreieck ist nicht rechtwinklig.

In der Praxis wird der Satz des Pythagoras, neben Sinus- und Kosinussatz, auch heute noch vor allem für das Vermessen von Gelände verwendet.

Kartesisches Koordinatensystem

Der Satz von Pythagoras liefert eine Formel für den Abstand zweier Punkte in einer Ebene, die durch ein kartesisches Koordinatensystem beschrieben wird. Sind zwei Punkte (x₀,y₀) und (x₁,y₁) gegeben, dann ist ihr Abstand c durch

$c = \sqrt{(x_1-x_0)^2 + (y_1-y_0)^2}$

gegeben. Hierbei wird ausgenutzt, dass die Koordinatenachsen senkrecht zueinander liegen. Dies kann analog auf mehrere Dimensionen erweitert werden und liefert den euklidischen Abstand. Z. B. für den dreidimensionalen Fall:

$c = \sqrt{(x_1-x_0)^2 + (y_1-y_0)^2 + (z_1-z_0)^2}$

Beweise

Für den Satz sind mehrere hundert verschiedene Beweise bekannt. Der Satz des Pythagoras ist damit der meistbewiesene mathematische Satz. Exemplarisch werden nachfolgend drei geometrische Beweise vorgestellt:

Geometrischer Beweis durch Ergänzung

Diagramm zum Ergänzungsbeweis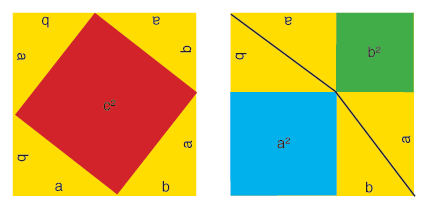

Positionierung von vier Dreiecken in einem Quadrat mit der Seitenlänge a + b

In ein Quadrat mit der Seitenlänge a + b werden vier gleiche (kongruente) rechtwinklige Dreiecke mit den Seiten a, b und c (Hypotenuse) eingelegt. Dies kann auf zwei Arten geschehen, wie im Diagramm dargestellt ist.

Die Flächen des linken und des rechten Quadrates sind gleich (Seitenlänge a + b). Das linke besteht aus den vier rechtwinkligen Dreiecken und einem Quadrat mit Seitenlänge c, das rechte aus den gleichen Dreiecken sowie einem Quadrat mit Seitenlänge a und einem mit Seitenlänge b. Die Fläche c² entspricht also der Summe der Fläche a² und der Fläche b², also a² + b² = c². Dies ist der Satz des Pythagoras.

Eine algebraische Lösung ergibt sich aus dem linken Bild. Das große Quadrat hat die Seitenlänge a+b, und somit die Fläche (a + b)². Zieht man von dieser Fläche die 4 Dreiecke ab, die jeweils eine Fläche von ab/2 (also insgesamt 2ab) haben, so bleibt die Fläche c² übrig. Es ist also (a + b)² = 2ab + c². Aus Auflösung der Klammer folgt a² + 2ab + b² = 2ab + c². Zieht man nun auf beiden Seiten 2ab ab, bleibt der Satz des Pythagoras übrig.

Scherungsbeweis

Diagramm zum Scherungsbeweis

Zweifache Scherung der Kathetenquadrate und Drehung in das Hypotenusenquadrat

Diagramm zum Beweis mit Ähnlichkeiten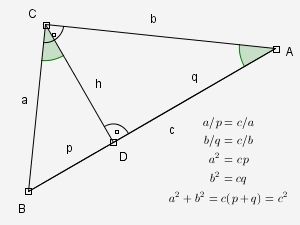

Ähnlichkeit der Dreiecke ACB, CBD und ACD

Eine Möglichkeit ist die Scherung der Kathetenquadrate in das Hypotenusenquadrat. Unter Scherung eines Rechtecks versteht man in der Geometrie die Überführung des Rechtecks in ein Parallelogramm unter Beibehaltung der Höhe. Bei der Scherung ist das sich ergebende Parallelogramm zu dem Ausgangsrechteck flächengleich. Über zwei Scherungen können die beiden kleineren Quadrate dann in zwei Rechtecke umgewandelt werden, die zusammen genau in das große Quadrat passen.

Beim exakten Beweis muss dann noch über die Kongruenzsätze im Dreieck nachgewiesen werden, dass die kleinere Seite der sich ergebenden Rechtecke jeweils den Hypotenusenabschnitten entspricht. Wie üblich wurden in der Animation die Höhe mit h, die Hypotenusenabschnitte mit p und q bezeichnet.

Beweis mit Ähnlichkeiten

Es ist nicht unbedingt notwendig, zum Beweis des Satzes von Pythagoras Flächen heranzuziehen. Geometrisch eleganter ist es, Ähnlichkeiten zu verwenden.

Sobald man sich durch Berechnung der Winkelsummen im Dreieck überzeugt hat, dass die beiden grünen Winkel im unteren Bild gleich groß sein müssen, sieht man, dass die Dreiecke ACB, CBD und ACD ähnlich sind. Der Beweis des Satzes von Pythagoras ergibt sich dann wie im Bild gezeigt.

Diese Herleitung lässt sich anschaulich mit der Ähnlichkeit der Quadrate und der Ähnlichkeit deren angrenzender Dreiecke erklären. Da diese proportional zur Fläche der jeweils anliegenden Quadrate sind, repräsentiert die Gleichung CBD + ACD = ACB den Satz.

Pythagoreische Tripel

→ Hauptartikel: Pythagoreisches Tripel

Unter allen Dreiergruppen (a,b,c), die die Gleichung a² + b² = c² erfüllen, gibt es welche, bei denen a, b und c jeweils ganze Zahlen sind. Diese Dreiergruppen werden pythagoreische Tripel genannt. Das einfachste solche Tripel bilden die Zahlen 3, 4 und 5 (wegen 3² + 4² = 5², also 9 + 16 = 25). Pythagoreische Tripel werden seit altersher zur Konstruktion rechtwinkliger Dreiecke verwendet. Ein Beispiel ist die Zwölfknotenschnur, mit der ein Dreieck gelegt wird, dessen Seiten die Längen 3, 4 und 5 haben. Die beiden kurzen Seiten bilden dann einen rechten Winkel.

Verallgemeinerungen

Kosinussatz

Der Kosinussatz ist die Verallgemeinerung des Satzes von Pythagoras für beliebige Dreiecke:

$c^2 = a^2 + b^2 - 2ab\cdot\cos\gamma$

wobei γ der Winkel zwischen a und b ist. Der Kosinussatz unterscheidet sich also durch den Term 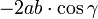$- 2ab\cdot\cos\gamma$ vom Satz des Pythagoras. Da der Kosinus von 90° gleich null ist, fällt dieser Term bei einem rechten Winkel weg und es ergibt sich der Satz des Pythagoras.

Gilt umgekehrt die Beziehung c² = a² + b², so muss 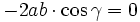$- 2ab\cdot\cos\gamma = 0$ sein. Daraus folgt 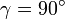$\gamma = 90^\circ$. In diesem Fall ist das Dreieck also rechtwinklig.

Verallgemeinerung auf beliebige Dreiecke ohne Winkelfunktionen

Es ist auch möglich, die Aussage des Kosinussatzes ohne Winkelfunktionen zu erhalten. Dazu konstruiert man ein beliebiges Dreieck mit Zirkel und Lineal folgendermaßen: Wir zeichnen die Seite c zwischen den Punkten A und B. Dann tragen wir mit dem Zirkel die Kathetenlänge b von A aus in Form einer Kreislinie auf, die c schneidet. Von B aus tragen wir nun die Kathetenlänge a in Form einer Kreislinie auf, die ebenfalls c schneidet. Wir sehen, dass c durch die beiden Kreislinien in insgesamt drei Teile zerschnitten wird.

Jene Teilstrecke auf c, die in A beginnt, nennen wir x, den mittleren Abschnitt nennen wir u und jenen Teil, der in B endet, nennen wir y, so dass gilt: c = x + u + y. Dann gilt: a = u + y, b = u + x, c = u + x + y, und c² = (u + x + y)² = u² + x² + y² + 2ux + 2uy + 2xy.

Für jedes Dreieck gilt nun: c² = a² + b² − u² + 2xy; für rechtwinklige Dreiecke gilt u² = 2xy, so dass sich für den Spezialfall der rechtwinkligen Dreiecke der Ausdruck reduziert auf c² = a² + b². Natürlich gilt auch: u² − 2xy = 2abcos(γ) oder cos(γ) = (u² − 2xy) / 2ab, da c² = a² + b² − u² + 2xy dieselbe Aussage macht wie der Kosinussatz, nur eben ohne Winkelfunktionen. Man kann beweisen, dass für jedes u eines Dreiecks mit 3 ganzzahligen Seiten, für welches eine Beziehung der Form a^p + b^p = c^p für p > 2 erfüllt ist (vgl. bereits bewiesener Großer Fermatscher Satz), gilt: u = 6k für p=3 und u = 6kp für p>3, k aus N.

Aus der notwendigen Gleichung u² = 2xy für rechtwinklige Dreiecke ergibt sich übrigens eine sehr einfache Vorschrift zur Ermittlung ganzzahliger pythagoreischer Zahlentripel, da sich die Größen a, b und c aus den Lösungen u, x und y (s.o.) zusammensetzen.

Innenprodukträume

Abstrahiert man vom gewöhnlichen euklidischen Raum, so erhält man Innenprodukträume, also Vektorräume mit einem Skalarprodukt. Hier gilt die folgende Aussage: Gegeben seien zwei Vektoren v und w. Sind die beiden orthogonal, stehen also senkrecht aufeinander, so gilt:

$\|{\mathbf v} + {\mathbf w}\|^{2} = \|{\mathbf v}\|^{2} + \|{\mathbf w}\|^{2}.$

Dabei bezeichnet 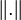$\| . \|$ die Norm des Raums. Da v+w die Hypotenuse des von v und w aufgespannten Dreiecks ist, steht hier wieder der Satz des Pythagoras, allerdings in abstrakten mathematischen Gebilden wie unendlich dimensionalen Funktionenräumen. Die Umkehrung gilt ebenfalls. Trifft die obige Gleichung zu, so stehen die beiden Vektoren senkrecht aufeinander.

Man kann die Aussage noch weiter verallgemeinern. Sei S = u₁,...,u_n ein Orthogonalsystem mit endlich vielen Elementen, d. h. alle Vektoren u_k stehen orthogonal aufeinander. Dann gilt

$\left\| \sum_{k=1}^n u_k \right\|^2 = \sum_{k=1}^n \| u_k \|^2.$

Der Beweis ist einfach. Denn die Norm des Innenproduktraums ist 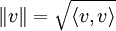$\| v \| = \sqrt{ \langle v, v \rangle }$, und mit der Linearität des Innenprodukts sowie der Orthogonalität gilt

$\left\| \sum_{k=1}^n u_k \right\|^2 = \left\langle \sum_{k=1}^n u_k, \sum_{l=1}^n u_l \right\rangle= \sum_{k=1}^n \sum_{l=1}^n \langle u_k, u_l \rangle = \sum_{k=1}^n \langle u_k, u_k \rangle = \sum_{k=1}^n \| u_k \|^2.$

Um eine Aussage über unendliche Summen zu gewinnen, betrachtet man eine Orthogonalfolge (u_k), d. h. eine Folge, deren Glieder alle orthogonal zueinander sind. Konvergiert die Reihe 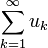$\sum_{k=1}^\infty u_k$, so konvergiert auch 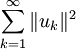$\sum_{k=1}^\infty \| u_k \|^2$ und es gilt

$\left\| \sum_{k=1}^\infty u_k \right\|^2 = \sum_{k=1}^\infty \| u_k \|^2.$

Der Beweis der zweiten Behauptung folgt aus der Stetigkeit des Innenprodukts. Eine weitere Verallgemeinerung führt zur Parsevalschen Gleichung.

Nichteuklidische Geometrie

Nichteuklidische Geometrien sind Geometrien, in denen das Parallelenaxiom nicht gilt. Ein Beispiel hierfür ist die Geometrie der Kugeloberfläche. Dort gilt der Satz des Pythagoras nicht mehr, da in solchen Geometrien der Innenwinkelsatz nicht gilt, also die Winkelsumme eines Dreiecks von 180° verschieden ist.

Geschichte

Babylon und Indien

Bereits auf einer babylonischen Keilschrifttafel (Britisches Museum 85196, London), die in die Zeit der Hammurabi-Dynastie datiert wird (ca. 1829 bis ca. 1530 v. Chr), findet sich eine geometrische Problemstellung mit Lösung, bei der der Satz zur Berechnung von Längen (im Sexagesimalsystem) verwendet wurde:^[1]

Ein Balken, 0;30 (30/60 GAR = 1/2 GAR ≈ 3 m ^[2] lang.)

Von oben ist er 0;6 (6/60 GAR) herabgekommen.

Von unten was hat er sich entfernt?

0;30 (30/60) quadriere, 0;15 (900/3600 = 15/60) siehst du.

0;6 (6/60) von 0;30 (30/60) abgezogen, 0;24 (24/60) siehst du.

0;24 (24/60) quadriere, 0;9,36 (576/3600) siehst du.

0;9,36 (576/3600) von 0;15 (900/3600) ziehe ab, 0;5,24 (324/3600) siehst du.

0;5,24 (324/3600) hat was als Quadratwurzel ? 0;18 (18/60).

0;18 (18/60 GAR) am Boden hat er sich entfernt.

Daraus ergibt sich: 0;18² = 0;30² − 0;24², also a² = c² − b² bzw. a² + b² = c².

Ein Interesse an einem mathematischen Beweis wurde in den babylonischen Quellen jedoch nicht gefunden.

Die Keilschrifttafel Plimpton 322 enthält außerdem 15 verschiedene pythagoreische Tripel, u. a. (56,90,106), (119,120,169) sowie (12709,13500,18541), was auf ein Verfahren zur Berechnung solcher Tripel schließen lässt.

Auch im indischen Baudhayana-Sulba-Sutra aus dem 6. Jahrhundert v. Chr. finden sich fünf pythagoreische Tripel. Der Lehrsatz wurde auch in Indien benutzt, so etwa im Apastamba-Sulba-Sutra, aber nicht bewiesen.^[3]

China

Auch in China war der Satz schon sehr früh bekannt. Sein chinesischer Name ist gou-gu. Ein unter dem Namen hsuan-shu bekanntes Diagramm, das einen graphischen Beweis am Beispiel des Dreiecks mit den Seiten 3, 4 und 5 zeigt, findet sich in der Schrift Zhoubi suanjing („Klassiker des Gnomons“).^[4] Auch im Chiu chang suan shu („Neun Kapitel über die Kunst der Mathematik“, 3. Jahrhundert v. Chr.), dem klassischen mathematischen Werk Chinas mit einer Sammlung von 263 Anleitungen zum Lösen von Aufgaben, wird er angewendet. Liu Hiu (3. Jahrhundert n. Chr.) gibt in seinem Kommentar Jiuchang suan shu zu den „Neun Kapiteln“ im neunten Kapitel einen Zerlegungsbeweis an.

Die umstrittene Rolle des Pythagoras

Büste des Pythagoras; Kapitolinische Museen, Rom

Die Benennung des Satzes nach dem griechischen Philosophen Pythagoras (6. Jahrhundert v. Chr.) ist erst in späten Quellen bezeugt. Daher ist in der Forschung die Frage nach der Rolle des Pythagoras stark umstritten. Verschiedene Hypothesen kommen in Betracht:

• Pythagoras übernahm den Satz von den Babyloniern, seine Rolle war nur die eines Vermittlers orientalischen Wissens an die Griechen. Antiken Quellen zufolge unternahm er eine Ägyptenreise, er soll sogar in Babylonien gewesen sein, doch ist die Glaubwürdigkeit der Berichte über seine Reisen umstritten.
• Pythagoras hat den Satz unabhängig von der orientalischen Mathematik entdeckt und auch erstmals bewiesen. Diese Ansicht war in der Antike verbreitet.
• Pythagoras verdankte die Kenntnis des Sachverhalts orientalischen Quellen, war aber der erste, der einen Beweis dafür fand. Tatsächlich waren Babylonier und Ägypter anscheinend nur an der Anwendung des Satzes für praktische Zwecke, nicht an einem allgemeingültigen Beweis interessiert. So enthält beispielsweise das älteste bekannte Rechenbuch der Welt, das ägyptische Rechenbuch des Ahmes (auch Papyrus Rhind) aus dem 17. Jahrhundert v. Chr., bereits komplizierte Aufgaben, es fehlt jedoch jede Verallgemeinerung, es wird nicht definiert und bewiesen.
• Pythagoras hat in der Geschichte des Satzes keine Rolle gespielt; erst spätere Pythagoreer haben möglicherweise den ersten Beweis gefunden.

Gegensätzliche Positionen vertreten die Wissenschaftshistoriker Walter Burkert und Leonid Zhmud. Burkert zieht allenfalls eine Vermittlerrolle des Pythagoras in Betracht, Zhmud schreibt ihm mathematische Leistungen wie den Beweis des Satzes zu und betont seine Eigenständigkeit gegenüber der orientalischen Mathematik.^[5]

Euklid, der in der zweiten Hälfte des 4. Jahrhunderts v. Chr. in seinem berühmten Werk Elemente das mathematische Wissen seiner Zeit zusammentrug, bot einen Beweis, brachte den Satz aber nicht mit Pythagoras in Zusammenhang. Der älteste Beleg dafür, dass der Satz mit Pythagoras in Verbindung gebracht wurde, ist ein Epigramm eines Apollodoros, der möglicherweise mit dem Philosophen Apollodoros von Kyzikos zu identifizieren ist; in diesem Fall stammen die Verse aus der zweiten Hälfte des 4. Jahrhunderts v. Chr. Der Text lautet:

Als Pythagoras einst die berühmte Zeichnung gefunden,

Brachte als Opfer er dar herrliche Stiere dem Gott.

Apollodoros gibt nicht an, welche "berühmte" Zeichnung oder Figur er meint, doch Diogenes Laertios (3. Jahrhundert n. Chr.), der die beiden Verse zitiert, ging davon aus, dass es sich um den "Satz des Pythagoras" handelt. Diese Überlieferung, wonach Pythagoras einem Gott zum Dank dafür, dass dieser ihm die Erkenntnis eingab, ein Rinderopfer darbrachte, steht in Widerspruch zu dem von zahlreichen antiken Quellen überlieferten Umstand, dass Pythagoras und die Pythagoreer Tieropfer grundsätzlich ablehnten.

Rezeption

Der Satz des Pythagoras gehört zu den bekanntesten mathematischen Sätzen. Die antike Legende von dem Rinderopfer, das Pythagoras zum Dank für die Erkenntnis dargebracht haben soll, inspirierte den Dichter Adelbert von Chamisso zu einem Sonett:

Vom pythagoreischen Lehrsatz

Die Wahrheit, sie besteht in Ewigkeit,

Wenn erst die blöde Welt ihr Licht erkannt;

Der Lehrsatz nach Pythagoras benannt

Gilt heute, wie er galt zu seiner Zeit.

Ein Opfer hat Pythagoras geweiht

Den Göttern, die den Lichtstrahl ihm gesandt;

Es taten kund, geschlachtet und verbrannt,

Einhundert Ochsen seine Dankbarkeit.

Die Ochsen seit dem Tage, wenn sie wittern,

Daß eine neue Wahrheit sich enthülle,

Erheben ein unmenschliches Gebrülle;

Pythagoras erfüllt sie mit Entsetzen;

Und machtlos sich dem Licht zu widersetzen

Verschließen sie die Augen und erzittern.

Literatur

• Egmont Colerus: Vom Einmaleins zum Integral. Mathematik für Jedermann. Rowohlt, Reinbek 1982. ISBN 3-499-16692-5
• Anna M. Fraedrich: Die Satzgruppe des Pythagoras. Spektrum Akademischer Verlag, Heidelberg 1994. ISBN 3-86025-669-6
• H.L. Resnikoff, R.O. Wells Jr.: Mathematik im Wandel der Kulturen. Vieweg, Braunschweig/Wiesbaden 1983. ISBN 3-528-03578-1
• Hans Schupp: Elementargeometrie. UTB, Stuttgart 1977. ISBN 3-506-99189-2
• Simon Singh: Fermats letzter Satz. dtv, München 2000. ISBN 3-423-33052-X
• Heinrich Tietze: Mathematische Probleme. Gelöste und ungelöste mathematische Probleme aus alter und neuer Zeit. Vierzehn Vorlesungen für Laien und Freunde der Mathematik. C.H. Beck, München 1990. ISBN 3-406-02535-8
• Alexander K. Dewdney: Reise in das Innere der Mathematik. Birkhäuser, Berlin 2000. ISBN 3-7643-6189-1
• Eli Maor: The Pythagorean Theorem: A 4,000-year History. Princeton University Press 2007, ISBN 0691125260

Weblinks

• Vielzahl animierter Beweise des Satzes von Pythagoras, Landesbildungsserver Baden-Württemberg
• Beweise für den Satz des Pythagoras
• Beweissammlung für den Satz des Pythagoras auf cut-the-knot (englisch)
• Java-Applets (englisch)
• Interaktives Lernprogramm mit Beweisen, Aufgaben und vielen Links
• Eric W. Weisstein: Pythagorean theorem auf MathWorld (englisch) (enthält auch verschiedene Beweise)

Einzelnachweise

1. ↑ Helmuth Gericke: Mathematik in Antike und Orient, Berlin 1984, S. 33f.; Kurt Vogel: Vorgriechische Mathematik. Teil II: Die Mathematik der Babylonier, Hannover und Paderborn 1959, S. 67f.
2. ↑ Kurt Vogel: Vorgriechische Mathematik. Teil II: Die Mathematik der Babylonier. Schroedel, Hannover und Schöningh, Paderborn 1959; S. 20.
3. ↑ Helmuth Gericke: Mathematik in Antike, Orient und Abendland, Wiesbaden 2005, S. 68; Oskar Becker, Das mathematische Denken der Antike, Göttingen 1966, S. 55f. Ausführliche Darlegung des Sachverhalts bei Thomas L. Heath, The thirteen books of Euclid's Elements, Bd. 1, 2. Auflage, New York 1956, S. 360-364.
4. ↑ Oskar Becker, Das mathematische Denken der Antike, Göttingen 1966, S. 56.
5. ↑ Walter Burkert, Weisheit und Wissenschaft, Nürnberg 1962, S. 405f., 441ff.; Leonid Zhmud, Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin 1997, S. 141-151, 160-163. Siehe auch Thomas L. Heath, The thirteen books of Euclid's Elements, Bd. 1, 2. Auflage, New York 1956, S. 350-360.