- Pythagoräisches Komma
-
Musikalische Intervalle Prime
Sekunde
Terz
Quarte
Quinte
Sexte
Septime
Oktave
None
Dezime
Undezime
Duodezime
TredezimeSpezielle Intervalle Mikrointervall
Komma
Diësis
Limma
Apotome
Halbton/Ganzton
Ditonus
Tritonus
WolfsquinteEinheiten Cent
Millioktave
SavartDas Pythagoreische Komma ist in der Musik ein Intervall von etwa einem Achtelton, welches nicht als selbstständiger musikalischer Tonschritt gebraucht wird. Es ist in reiner Stimmung der Unterschied von sieben Oktaven zu zwölf Quinten und eher von musiktheoretischer Bedeutung. Praktische Relevanz erhält es beim Stimmen von Instrumenten mit festen Tonhöhen wie zum Beispiel Tasteninstrumenten oder Saiteninstrumenten mit Bünden.
Als erster definierte der Pythagoreer Philolaos das pythagoreische Komma. Die erste Berechnung der Komma-Proportion als 531441:524288 findet sich bei Euklid; ihr liegt die Oktave mit Proportion 2:1 und die reine Quinte mit Proportion 3:2 zugrunde.
Anschauliche Herleitung
Die Bedeutung des Pythagoreischen Kommas geht aus folgender Tabelle hervor, in der gemäß der Quintenspirale zwölf reine Quinten aufeinander gesetzt werden. Diese haben je ein Frequenzverhältnis von 2:3. Daneben sind sieben Oktaven aufeinander gesetzt. (Im Beispiel wird C als Grundton verwendet).
Ton Quinte Frequenzverhältnis entspricht C 0 1 : 1 = 1 : 1 G 1 2 : 3 = 1 : 1,5 D 2 4 : 9 = 1 : 2,25 A 3 8 : 27 = 1 : 3,375 E 4 16 : 81 = 1 : 5,0625 H 5 32 : 243 = 1 : 7,59375 Fis 6 64 : 729 = 1 : 11,390625 Cis 7 128 : 2187 = 1 : 17,0859375 Gis 8 256 : 6561 = 1 : 25,62890625 Dis 9 512 : 19683 = 1 : 38,443359375 Ais 10 1024 : 59049 = 1 : 57,6650390625 Eis 11 2048 : 177147 = 1 : 86,49755859375 His (≈ C) 12 4096 : 531441 = 1 : 129,746337890625 Ton Oktave Frequenzverhältnis C 0 1 : 1 C 1 1 : 2 C 2 1 : 4 C 3 1 : 8 C 4 1 : 16 C 5 1 : 32 C 6 1 : 64 C 7 1 : 128 Der Unterschied der beiden Töne (letzte in den Tabellen) ergibt ein Frequenz-Verhältnis von
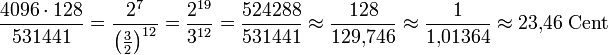 .
.Das Intervall mit diesem Verhältnis wird Pythagoreisches Komma genannt.
Das Pythagoreische Komma als Problem beim Stimmen von Tasteninstrumenten
Ein Instrument (wie die modernen Tasteninstrumente), das pro Oktave nur zwölf verschiedene Töne erzeugen kann, lässt sich nicht so stimmen, dass es in allen Tonarten mit absolut reinen Intervallen gespielt werden kann. In der Praxis wird versucht, beim Stimmen von Musik-Instrumenten dieses pythagoreische Komma, also diesen „Fehler“, möglichst sinnvoll auf alle Töne zu verteilen. Nach verschiedenen Theorien ergeben sich dann die verschiedenen musikalischen Stimmungen. Es gab auch Versuche mit Tasteninstrumenten, deren Oktave mehr als zwölf Töne umfasst (z. B. geteilte schwarze Tasten).
Zwölf reine Quinten (2:3) ergeben 8423,46 Cent, sieben Oktaven dagegen nur 8400 Cent. Damit sich in gleichstufig-temperierter Stimmung die Quintenspirale nach sieben Oktaven zum Quintenzirkel schließt, muss das Pythagoreische Komma beim Stimmen auf die zwölf Quinten verteilt werden. Damit wird die reine Quinte von 701,9550 Cent um 1,9550 Cent auf 700 Cent verkleinert.
Reine Quinte:
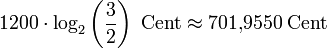 .
.
Wikimedia Foundation.
