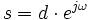QAM

Quadraturamplitudenmodulation (Abkürzung: QAM, engl: Quadrature Amplitude Modulation) ist eine Modulationsart in der elektronischen Nachrichtentechnik, die Amplitudenmodulation und Phasenmodulation miteinander kombiniert. Dabei werden derselben Trägerschwingung zwei voneinander unabhängige Signale aufgeprägt. Im Prinzip werden die Signale jeweils per Amplitudenmodulation auf einen Träger gleicher Frequenz, jedoch mit um 90° verschobener Phase, moduliert. Anschließend werden die beiden derart modulierten Trägerschwingungen addiert.

Zur Demodulation ist – im Unterschied zu z. B. der beim Rundfunk auch benutzten Amplitudenmodulation (AM) – das Trägersignal in gleicher Phase wie beim Sender vonnöten; es muss also aus dem Empfangssignal rekonstruierbar sein – was bei der Kodierung der übertragenen Signale berücksichtigt werden muss.

In der Fernsehtechnik wird in der Regel die Bezeichnung Quadraturmodulation verwendet.

Anwendung

Die erste allgemein bekannte Anwendung findet sich bei der Übertragung der beiden Farbdifferenzsignale beim analogen Farbfernsehen nach dem NTSC- bzw. (in modifizierter Form) nach dem PAL-Verfahren. Heute besteht die Hauptanwendung in der Übertragung digitaler Daten über einen analogen, rauschbelasteten Frequenzkanal. Bekannte Anwendungsbeispiele sind die DSL-Technik oder DVB-T. Für die Übertragung von Daten über HF-Netze (Internet über Fernsehkabel) wird ebenfalls QAM als Modulationsverfahren eingesetzt.

Weitere Anwendungen bzw. genauere Ausführungen folgen am Ende dieses Artikels.

Mathematischer Hintergrund

1. Zwei Sinuskurven, die zueinander um 90° ( = 1 / 4 Wellenlänge) phasenverschoben sind (gleichbedeutend einer Sinus- und einer Cosinuskurve), werden untereinander gezeichnet. Überall dort, wo eine der Kurven ein Maximum oder Minimum hat, hat die jeweils andere einen Nulldurchgang.
   
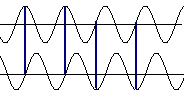
2. Bei einem amplitudenmodulierten Signal lässt sich durch Betrachten der Maxima das ursprüngliche Signal erkennen. Die Nulldurchgänge werden vom Signal nicht beeinflusst.
   
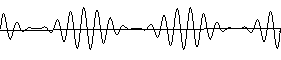
3. Durch die addititive Überlagerung von zwei amplitudenmodulierten Signalen, die gemäß (1) um 90° phasenverschoben sind, entsteht eine kompliziert anmutende Kurve, eben das quadraturmodulierte Signal.
4. Wenn man die ursprüngliche unmodulierte Sinus-Kurve zum Vergleich nimmt und nur an den Stellen, an denen die Sinuskurve Maxima hat, die Werte der quadraturmodulierten Kurve betrachtet, erkennt man genau die Werte der amplitudenmodulierten Sinus-Kurve wieder.
   Genauso erkennt man an den Maxima der Cosinus-Kurve die entsprechenden Werte der amplitudenmodulierten Cosinus-Kurve wieder.
   Der Grund ist, dass (wie in (2) erklärt) die jeweils andere Kurve an den betrachteten Stellen überhaupt keinen Einfluss auf die quadraturmodulierte Kurve hat.

Wie in der Einleitung schon angedeutet, ist – im Gegensatz zur einfachen Amplitudenmodulation – wichtig, dass beim Empfang (Demodulation) des quadraturmodulierten Signals der ursprüngliche unmodulierte Träger mit der richtigen Phasenlage zur Verfügung steht. Aus diesem Grunde ist eine präzise Träger-Regenerierung notwendig.

Digitale Modulationstechnik

Der digitale Datenstrom wird in zwei Signale aufgeteilt, die dem Träger aufmoduliert werden. Der Anschaulichkeit halber jedoch betrachten wir zunächst nicht diese beiden Einzelsignale, sondern eine zweidimensionale Repräsentation – ehe wir den beiden Signalen weiter unten als „I“- und „Q“-Signal wiederbegegnen.

Lissajous-Figur der Komponenten „I“ und „Q“ eines realen 4-QAM-Signals in einem etwas verzerrten und leicht verrauschten Übertragungskanal. Zu erkennen sind die vier Signalpunkte als etwas dichtere „Wölkchen“ sowie die Übergänge zwischen den Punkten als Verbindungslinien. Dieses 4-QAM-Signal wird auch als QPSK-Signal bezeichnet. Es wurde von einem DVB-S-Satelliten ausgesendet.

Gedanklich wird durch Amplitude und Phase als Polarkoordinaten eine 2-dimensionale Ebene aufgespannt, in der eine Anzahl von Punkten (z. B. vier Punkte im Bild rechts) – eine sog. Konstellation von Signalpunkten – festgelegt wird, welche voneinander einen Mindestabstand und einzeln eine maximale Energie haben. Im Empfänger wird die Lage der Punkte festgestellt und damit die aus Phase und Amplitude gewonnene Information zurückgewonnen.

Die erwähnte „Ebene“ ist zwar eine gedankliche Konstruktion; aber man kann diese Ebene, um sie anschaulich zu machen, ganz konkret aufbauen: Als Bildschirm eines Oszilloskops. „Amplitude“ ist dann der Abstand eines aus der Mitte heraus ausgelenkten Lichtpunktes zum Mittelpunkt des Bildschirms. Die „Phase“ ist die Richtung (als Winkel dargestellt), in die der Lichtpunkt ausgelenkt wird. Ein Quadraturmodulator ist dann eine Schaltung, mit der man den Lichtpunkt auf Punkte lenken kann, denen beispielsweise Buchstaben zugeordnet sind. Die Reihenfolge, mit denen der Lichtpunkt auf die Buchstaben zeigt, kann dann zum Beispiel ein Wort beschreiben. Da der Strahl aber oft auf mehrere Millionen Punkte pro Minute zeigt, braucht man ein elektronisches Gerät, das diesem Signal schnell genug folgen kann. Das ist der Quadraturdemodulator, dem das Signal aber nicht über ein Oszilloskop als Umweg zugeführt wird, sondern direkt.

Ist das Signal Störungen wie Rauschen und Verzerrungen ausgesetzt, kann es im Empfänger zu fehlerhaften Dekodierungen kommen. (Der Lichtpunkt trifft dann im Raster auf dem Bildschirm die Punkte nicht mehr genau. Bei Bildschirmen, die ein bisschen nachleuchten, entsteht dann anstelle des Punktes eine kleine „Wolke“.) Deswegen wird die Quadraturamplitudenmodulation häufig mit Verfahren kombiniert, mit denen sich Fehler erkennen und teilweise sogar korrigieren lassen.

Abgetastet wird das Signal mit einer zur Bandbreite reziproken Taktfrequenz. Man kann so pro Zeitintervall einen Signalpunkt übertragen.

„I“ und „Q“

Bei der Quadraturamplitudenmodulation werden von einem gemeinsamen Generator zwei Sinusschwingungen erzeugt: „Inphase“ und „Quadratur“, oder kurz: „I“ und „Q“. Beide Signale haben die gleiche Frequenz. Der Unterschied zwischen beiden Signalen besteht darin, dass „Q“ gegenüber „I“ in der Phase um 90° verschoben ist; daher spricht man auch von Sinus- und Cosinusschwingung. Quadratur lässt sich als Viertelkreis verstehen, wodurch der Winkel 90° entsteht.

Da ihnen Informationen aufmoduliert werden, nennt man die beiden Schwingungen Träger, und die gemeinsame Frequenz ist die Trägerfrequenz. Beide Trägerschwingungen durchlaufen jeweils einen Amplitudenmodulator.

Dabei ist zu beachten, dass die Amplitude von Sinus- und Cosinusschwingung bei der Demodulation unabhängig wiedergewonnen werden können. (Wozu die Phasenlage des Trägers bekannt sein muss.) Man sagt auch, die beiden Schwingungen seien orthogonal. Gedanklich kann man sich die Amplituden der beiden Schwingungen auch als kartesische Koordinaten in der oben angedeuteten Ebene vorstellen, auch „I“- und „Q“-Koordinate genannt.

In der einfachsten Implementierung von QAM gilt:

• Bei 4-QAM (QPSK, Quadrature Phase Shift Keying) kann jeder Träger zur Darstellung von einem Bit (2 Stufen) mit den Faktoren −1 und 1 multipliziert werden.
• Bei 16-QAM kann jeder Träger zur Darstellung von 2 Bits (4 Stufen) mit den Faktoren −3, −1, 1 und 3 multipliziert werden.
• Bei 32-QAM kann jeder Träger zur Darstellung von ca. 2,5 Bits (6 Stufen) mit den Faktoren −5, −3, −1, 1, 3 und 5 multipliziert werden.
• Bei 64-QAM kann jeder Träger zur Darstellung von 3 Bits (8 Stufen) mit den Faktoren −7, −5, −3, −1, 1, 3, 5 und 7 multipliziert werden.
• usw.

Nach der Modulation werden die beiden modulierten Träger addiert und in den technisch notwendigen Arbeitsbereich skaliert. Diese skalierte Summe wird dann zur Sendestrecke weitergeleitet. Weil der eine Träger gegenüber dem anderen Träger um 90° verschoben ist, entsteht durch die Addition der beiden Träger ein als Vektor oder „Zeiger“ darstellbares Signal. Abhängig von den gewählten Multiplikationsfaktoren ist dabei die Länge (Amplitude) und der Winkel (Phase) dieses Vektors einstellbar. Man kann den Vektor damit auf verschiedene Punkte zeigen lassen und auf diese Art und Weise Daten übertragen.

Eine weitere in der Praxis oft verwendete Art der Beschreibung digital modulierter Signale erfolgt durch komplexe Zahlen. Die oben beschriebene Ebene ist dann die Ebene der komplexen Zahlen. Diese kann, wie bei der Vektorbeschreibung erläutert, mit einer Sinus- (I-Phase) und einer Cosinus-Funktion beschrieben werden. Es entsteht ein komplexer Zeiger s, der wie folgt beschrieben werden kann:

$s=d\cdot e^{j\omega}$

Der Unterschied dieser Art der Beschreibung zu den Vorangegangenen ist, dass man nur von einem komplexen Träger ausgeht (e^jω). Auf den Realteil dieses Trägers wird der Realteil des Sendesymbols d = a + jb aufmoduliert (In-Phase) und auf den Imäginärteil der Imaginärteil des Sendesymbols (Quadratur-Phase).

Konstellationen

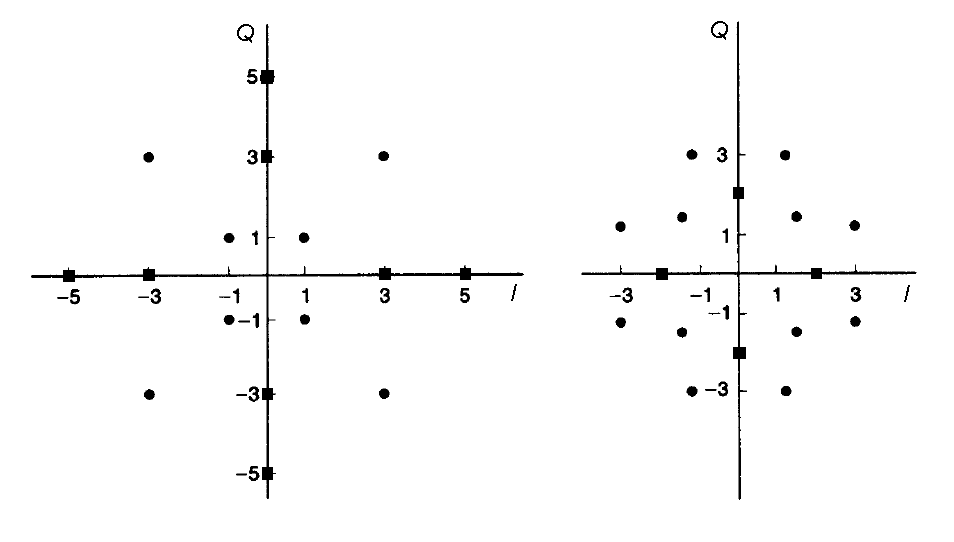Konstallationsmöglichkeiten für QAM-16 bei nicht orthogonaler Symbolanordnung. Die linke Anordnung wird bei der ITU-R Norm V.29 für Modemübertragungen mit maximal 9600bps verwendet.

Die Konstallationen der Symbole der diskreten QAM können verschiedenartig in der komplexen I/Q-Ebene angeordnet sein, dies wird in einem Konstellationsdiagramm dargestellt. Grundsätzlich wird bei QAM zwischen orthogonalen Rastern und nicht orthogonalen Rastern unterschieden. Die Anzahl der Symbole („Symbolpunkte“) in der komplexen I/Q-Ebene ist bei binären Übertragungen eine Zweierpotenz, um den einzelnen Symbolen eine bestimmte Anzahl an Bits zuzuordnen.

Beispiele für QAM-Konstallationen bei binärer Symbolzuordnung:

• 2 Bit: 4-QAM – diese ist identisch zur QPSK bzw. 4-PSK und verwendet 4 Punkte in einem 2x2-Raster bzw. auf einem Kreis.
• 4 Bit: Bei 16-QAM werden 16 Symbole verwendet, beispielsweise Anwendung bei ITU-R Norm V.29
• 6 Bit: Bei 64-QAM werden 64 Symbole verwendet
• 8 Bit: 256-QAM, Anwendung bei DVB-C
• 10 Bit: 1024-QAM
• 12 Bit: 4096-QAM. Dies ist die größte, im Rahmen der Spezifikation von DVB-C2 derzeit angedachte QAM-Konstellation, die unter besten Voraussetzungen – bei einem Störabstand von 36 dB – gerade noch detektierbar ist.

Im Fall einer ungeraden Anzahl von Bits pro Symbol wird die erforderliche Einordnung in das Zweierpotenz-Raster durch eine Reduktion desjenigen Konstellationsraumes erreicht, der durch die nächsthöhere Quadratzahl aufgespannt wird:

• 3 Bit: Bei 8-QAM sind das 8 Punkte (9 Punkte in einem 3×3-Raster weniger die Mittelposition ergeben die 8 benötigten Positionen – diese Modulation ist ähnlich zur 8-PSK)
• 5 Bit: Bei 32-QAM sind das 32 Punkte (36 Punkte in einem 6×6-Raster weniger je 1 Position pro Eckpunkt ergeben die 32 benötigten Positionen)
• 7 Bit: Bei 128-QAM sind das 128 Punkte (144 Punkte in einem 12×12-Raster weniger je 4 Position pro Eckpunkt ergeben die 128 benötigten Positionen)
• 9 Bit: Bei 512-QAM und darüber ist der Störabstand abhängig vom Übertragungsweg bereits so gering, dass diese Konstellationen nur bedingt (z. B. im Kabelnetz) eingesetzt werden können

Die nicht orthogonalen Rasteranordnungen bei QAM kann Vorteile bei der Symbolsynchronisation seitens Empfänger bieten. Weiters können bei hoher Fehlerrate vergleichsweise einfacher bestimmte Symbole aus dem Konstellationsdiagramm dynamisch entfernt werden, um so durch die damit verbundene Bitratenreduktion die Wahrscheinlichkeit von Übertragungsfehlern trotz schlechter Übertragungsqualität zu reduzieren. Der Nachteil aller nicht orthogonalen QAMs besteht im Vergleich zur orthogonalen Symbolanorndung in einer schlechteren spektrale Effizienz. Dies ist Folge der nicht geringst möglichen Packungsdichte der Symbolanordnung in der komplexe Ebene.

Begriffliche Unterscheidung zu QPSK

• 4-QAM und 4-PSK sind die gleiche Modulationsart. Bei vier Zuständen ergibt das Herangehen über QAM und PSK die gleichen Ergebnisse.
• 8-QAM und 8-PSK sind unterschiedliche, wenn auch ähnliche Modulationsarten. 8-PSK arbeitet mit konstantem Pegel, bei 8-QAM liegen die Zustände auf einem Quadrat. Technisch ist 8-PSK einfacher und effizienter zu realisieren, so dass 8-QAM keine Relevanz in der Praxis hat.
• 16-QAM und 16-PSK sind vollständig unterschiedliche Moduslationsarten. In den meisten Fällen ist 16-QAM wesentlich effizienter als 16-PSK. Ausnahmen sind Übertragungswege mit sehr hohem Amplituden-, aber geringem Phasenrauschen.

Codierung von Symbolen

Die Codierung realisiert die Umsetzung (mapping) des binären Datenstroms auf die Signalebene. Hierfür werden für eine M-QAM je log₂(M)-Bit pro QAM-Symbol verwendet.

Konstellationsdiagramm 4-QAM (entspricht exakt dem Konstellations- diagramm der QPSK)

Konstellationsdiagramm 16-QAM

Die binäre Codierung der Sendesymbole erfolgt, wie in den Abbildungen dargestellt, in Gray-Code (setzt Verwendung einer quadratischen Konstellation, also M = 2²ⁿ, voraus).

Um den Vorteil dieser Codierung zu verstehen, muss man betrachten, wie Fehler bei der Übertragung entstehen. Das Signal wird bei der Übertragung durch Rauschen überlagert. Das führt zu der oben beschrieben Streuung der Signalpunkte. Für übliche Wahrscheinlichkeitsverteilungen des Rauschens (z. B. Gauß-Verteilung) ist es am wahrscheinlichsten, dass der Signalpunkt in die Nähe eines direkt benachbarten Signalpunkt verschoben wird. Bei derartigen Fehlern wird bei der Gray-Codierung nur 1 Bit verändert. Dieser Fehler kann mit gängigen Fehlerkorrekturverfahren dann erkannt und bei ausreichend großem Hamming-Abstand der überlagerten Codierung auch korrigiert werden. Auf diese Weise kann die Bitfehlerrate bei der Übertragung über die verrauschte Leitung minimiert werden.

Auswahl der Konstellation

Die Zahl der Punkte ist durch die Störungen begrenzt, die für den Übertragungskanal erwartet werden. 4-QAM ist ziemlich „robust“. Man sieht in der Abbildung, dass sich die Punkte zwar aufweiten, sich aber noch nicht überlappen. Bei 32-QAM würden in der abgebildeten Störsituation schon Fehler auftreten. In gewissen Grenzen und um den Preis einer geringeren Netto-Datenrate kann man solche Fehler durch Vorwärtsfehlerkorrektur beseitigen. Deshalb wird QAM oft zusammen mit entsprechenden Fehlerkorrekturverfahren eingesetzt. Diese sind häufig Implementierungen des Viterbi-Algorithmus.

Analoge Modulation

Wie in der Einleitung schon angedeutet, gibt es QAM auch als analoge Modulation. Neben dem Einsatz dieses Verfahrens bei der PAL-Codierung wird die Quadraturamplitudenmodulation auch beim AM-Stereo-Verfahren verwendet.

Anwendung in der Fernsehtechnik

Beim Farbfernsehen müssen zusätzlich zum Helligkeits-Signal des Schwarzweiß-Fernsehens noch weitere Signale mit der Farbinformation übertragen werden (Farbartsignal F). Diese werden quadraturmoduliert und an geeigneter Stelle innerhalb des Frequenzspektrums des Schwarzweiß-Signals übertragen (siehe NTSC bzw. PAL). Um den bei der Quadraturamplitudenmodulation wichtigen Träger im Empfänger rekonstruieren zu können, wird er als sogenannter Burst in den wenigen Mikrosekunden dauernden Pausen zwischen den einzelnen Bildzeilen (horizontaler Strahlrücklauf) kurz nach dem Zeilensynchronimpuls übertragen. Dabei wird ein Oszillator im NTSC- bzw. PAL-Demodulator des Fernsehempfängers synchronisiert, der eine „Kopie“ des Trägersignals erzeugt, die dann auch während der Bildzeilen für die Demodulation zur Verfügung steht.

Literatur

• Hermann Rohling: Einführung in die Informations- und Codierungstheorie, Teubner Verlag, Stuttgart 1995, ISBN 3-519-06174-0.

Siehe auch

• Quadrature Phase Shift Keying
• Phasenmodulation

Technische Modulationsverfahren

Übersicht: Modulator 

Analoge Modulationsverfahren: AM | SSB | DSBSC | SSBSC | FM | PM | VM 

Digitale Modulationsverfahren: ASK | FSK | GFSK | QPSK | QAM | OFDM | DMT | TCM 

Pulsmodulationsverfahren: PWM | PAM | PFM | PPM | PCM 

Spezielle Modulationsverfahren: FHSS | DSSS 

Optische Modulationsverfahren: Allgemein | Polarisationsmodulatoren | Akustooptischer Modulator | Photoelastischer Modulator