- Quantenmechanischer Messprozess
-
In der Quantenmechanik ist jede Beobachtung eines mikroskopischen Messobjektes mit einer wesentlichen Veränderung von Eigenschaften des Objektes selbst verbunden. Damit stehen quantenmechanische Messungen im Gegensatz zur klassischen Messung an makroskopischen Objekten, bei denen die Beeinflussung der Eigenschaften des Objektes durch die Messung als unwesentlich angesehen werden kann.
Beim klassischen Messprozess kann bereits vor jeder Messung davon ausgegangen werden, dass ein Messergebnis existiert, welches im Rahmen der Messgenauigkeit mit sehr hoher Wahrscheinlichkeit (nahezu 1) eintreten wird, während alle anderen möglichen Messergebnisse sehr kleine Wahrscheinlichkeiten (nahezu 0) haben. Wiederholungen des gleichen Experimentes werden demnach im Rahmen der Messgenauigkeit immer dasselbe Ergebnis hervorbringen.
Für den quantenmechanischen Messprozess trifft diese Voraussetzung nicht mehr für jedes Messobjekt zu. Auch wenn das Messobjekt vor jeder Messung immer in demselben Zustand ist, kann hier vor der Messung nicht in jedem Fall davon ausgegangen werden, dass eine Wiederholung dieser Messung im Rahmen der Messgenauigkeit dasselbe Ergebnis hervorbringen wird.
Ein weiterer grundlegender Unterschied zwischen der quantenmechanischen Messung und dem klassischen Fall tritt bei der Messung von mehr als einer Eigenschaft eines Messobjektes hervor. Im klassischen Fall ist es unwesentlich, ob z. B. zuerst die Messung der Körpergröße und im Anschluss daran das Gewicht eines Menschen gemessen wird. Die jeweiligen Ergebnisse sind im Rahmen der Messgenauigkeit von der Reihenfolge der Messungen unabhängig. In ähnlicher Weise kann davon ausgegangen werden, dass die erste Messung das Resultat der zweiten Messung nicht, oder nur unbedeutend, beeinflussen wird. Diese Eigenschaften sind charakteristische Merkmale des klassischen Messprozesses.
Für den quantenmechanischen Messprozess haben diese „selbstverständlichen“ Merkmale hingegen keine Gültigkeit mehr. Im Falle der beiden Messgrößen Ort und Impuls eines Teilchens ist es beispielsweise von wesentlicher Bedeutung, in welcher Reihenfolge sie gemessen werden und es ergeben sich im Rahmen der Messgenauigkeit jeweils unterschiedliche Ergebnisse abhängig davon, wie diese Reihenfolge vom Experimentator gewählt wurde. Ein Hinweis darauf, wie sehr eine Beeinflussung der zweiten Messung durch die erste Messung zu erwarten ist, wird durch die heisenbergsche Unschärferelation repräsentiert.
Inhaltsverzeichnis
Präparation und Messung in der Quantenmechanik
Die theoretische Deutung eines Experimentes erfordert gemäß Heisenberg drei Schritte[1]:
- Es wird die experimentelle Ausgangssituation vorbereitet (Präparation) und durch eine Wellenfunktion beschrieben.
- Es findet eine zeitliche Entwicklung des physikalischen Systems statt. Die zeitliche Veränderung der Wellenfunktion wird durch die Schrödingergleichung beschrieben.
- Es wird die physikalische Messung am System vorgenommen (Registrierung). Die Wahrscheinlichkeit für ein bestimmtes Messergebnis kann aus der Wellenfunktion berechnet werden.
Oft wird in der Literatur bereits im ersten Schritt von einer Messung gesprochen. Es handelt sich bei diesem Schritt jedoch definitionsgemäß um eine Präparierung des Systems, welche nicht mit der anschließenden Registrierung verwechselt werden sollte. Besonders Lamb verweist in diesem Zusammenhang auf eine eindeutige Klärung, worin der erste Schritt des Prozesses genau bestehen soll, also nach Bohr die Fixierung der äußeren Bedingungen, durch welche die Ausgangssituation des betrachteten Systems definiert wird (z. B. ein Teilchen befindet sich mit Wahrscheinlichkeit 1 im Intervall der Länge Δx > 0).
Die Unterscheidung zwischen Präparation und Messung wird aus dem Charakter der jeweiligen Ergebnisse der beiden Schritte ersichtlich. Das Ergebnis einer einzelnen Messung ist ein Wert der Observablen (oder eine Eigenschaft). Bei Wiederholung der Messung erhält man bestenfalls eine Werte-Statistik für die fragliche Observable. Hingegen liefert die Präparation ein Wissen davon, mit welcher Wahrscheinlichkeit die Observable einen Wert (oder eine Eigenschaft) haben kann, und das für jede Observable[2].
Wenn in der Literatur von zwei unmittelbar aufeinanderfolgenden Messungen die Rede ist, so handelt es sich dabei meist um eine Präparation mit anschließender Registrierung des Messobjektes. Der Kenntnissgewinn durch die anfängliche Präparation wird in diesem Zusammenhang bereits als Messergebnis verwendet.
Formale Darstellung des Messprozess
Die Zustände eines mikroskopischen Objektes werden in der Quantenmechanik formal durch die normierten Vektoren
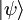 in einem abstrakten Vektorraum (Hilbertraum) beschrieben, d. h. das innere Produkt eines solchen Zustandes mit sich selbst ist 1. Ein derartiger Zustand repräsentiert beispielsweise ein Teilchen in einer Raumdimension und der Hilbertraum ist in diesem Fall der Raum der quadratintegrablen Funktionen über den reellen Zahlen. Das Skalarprodukt in diesem Hilbertraum wird dabei durch zwei eckige Klammern bezeichnet, d. h.
in einem abstrakten Vektorraum (Hilbertraum) beschrieben, d. h. das innere Produkt eines solchen Zustandes mit sich selbst ist 1. Ein derartiger Zustand repräsentiert beispielsweise ein Teilchen in einer Raumdimension und der Hilbertraum ist in diesem Fall der Raum der quadratintegrablen Funktionen über den reellen Zahlen. Das Skalarprodukt in diesem Hilbertraum wird dabei durch zwei eckige Klammern bezeichnet, d. h. 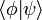 . Die Norm oder die „Länge“ von
. Die Norm oder die „Länge“ von 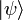 ist durch
ist durch 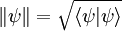 gegeben.
gegeben.In einem solchen Raum hat jeder Zustandsvektor eine eindeutige Darstellung in Form einer Orthonormalbasis
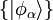
-
-
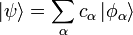 ,
,
-
mit komplexen Koeffizienten
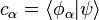 .
.Im Rahmen der statistischen Interpretation der Quantenmechanik repräsentiert der Zustandsvektor
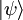 ein Ensemble von identisch präparierten Teilchen. Eine grundlegende Aussage der Quantenmechanik ist, dass jeder messbaren Observablen
ein Ensemble von identisch präparierten Teilchen. Eine grundlegende Aussage der Quantenmechanik ist, dass jeder messbaren Observablen 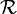 dieses Ensembles ein hermitescher Operator
dieses Ensembles ein hermitescher Operator 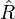 zugeordnet werden kann, wobei den Ergebnissen der Messungen dieser Observablen die reellen Eigenwerte
zugeordnet werden kann, wobei den Ergebnissen der Messungen dieser Observablen die reellen Eigenwerte 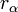 des Operators entsprechen. Formal ergeben sich diese Eigenwerte aus der zugrundeliegenden Eigenwertgleichung dieser Operatoren, d. h.
des Operators entsprechen. Formal ergeben sich diese Eigenwerte aus der zugrundeliegenden Eigenwertgleichung dieser Operatoren, d. h.Einige in der Quantenmechanik vorkommenden Operatoren haben kein abzählbares Spektrum, sondern ein kontinuierliches bzw. gemischtes Spektrum von Eigenwerten. Im kontinuierlichen Fall wird häufig die folgende symbolische Schreibweise verwendet
In Bezug auf den quantenmechanischen Messprozess sind die sogenannten Projektorwertigen Maße (engl.: projection-valued measure, häufig kurz PVM) von Bedeutung. Mit einem solchen Operator kann ein beliebiger Teil des Eigenwertspektrums einer Observable herausgefiltert bzw. ausgewählt werden (Selektion). Im Falle eines Teilchens im Einzelspaltexperiment wird beispielsweise durch den Spalt der Blende eine Menge von möglichen Teilchenbahnen aus dem kontinuierlichen Spektrum des Ortsoperators ausgesondert. Im Rahmen der Quantentheorie werden solche Projektionsoperatoren häufig durch eine Integraldarstellung repräsentiert
wobei A die betrachtete Teilmenge der Eigenwerte aus dem Spektrum des Operators ist, z. B. das Ortsintervall des Spaltes im Einzelspaltexperiment.
Für den Fall eines Punktspektrums wird der Projektionsoperator hingegen durch die Summe über ein abzählbares Spektrum von Eigenzuständen dargestellt
-
-
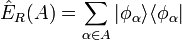 .
.
-
In diesem Fall ist A die entsprechende Indexmenge der Eigenwerte die bei der Projektion in Betracht gezogen werden.
- Für ein Quantenobjekt in einem beliebigen Zustand
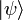 ist die Wahrscheinlichkeit
ist die Wahrscheinlichkeit 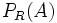 , für ein Messergebnis aus der Menge A, gegeben durch (Born 1926):
, für ein Messergebnis aus der Menge A, gegeben durch (Born 1926):
Diese Formel entspricht der statistischen Interpretation der Quantenmechanik.[3]
Die Wahrscheinlichkeit dafür, dass beispielsweise die Ortskomponente x eines Teilchens im Intervall [a,b] zu finden ist, ergibt demnach
wobei die übliche Schreibweise
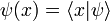 für die Darstellung der Wellenfunktion im Ortsraum verwendet wurde.
für die Darstellung der Wellenfunktion im Ortsraum verwendet wurde.Mit Hilfe der Projektionsoperatoren lässt sich im Rahmen der Quantenmechanik jeder Operator eindeutig in der sogenannten Spektraldarstellung repräsentieren
im kontinuierlichen Fall, sowie
im Falle des abzählbaren Spektrums.
- Führt man an einem System die Messung der Observablen
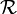 sehr oft aus, und ist vor jeder Messung das System immer im gleichen Zustand
sehr oft aus, und ist vor jeder Messung das System immer im gleichen Zustand 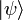 , so ist der Mittelwert
, so ist der Mittelwert 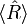 der Messergebnisse (Erwartungswert) gegeben durch (Born 1926):
der Messergebnisse (Erwartungswert) gegeben durch (Born 1926):
Dieser Zusammenhang zwischen Messprotokoll und den im mathematischen Kalkül der Quantentheorie vorkommenden Größen bestätigt sich in allen Experimenten.
Mit der Spektraldarstellung des Ortsoperators in x-Richtung
ergibt sich beispielsweise für Teilchen im Zustand
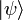 der Erwartungswert
der ErwartungswertDas Messproblem
Man betrachte ein Quantenobjekt, welches zu Beginn im Eigenzustand
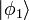 eines Operators R ist, und der die zu messende Observable repräsentiert. Der entsprechende Messwert (Eigenwert) sei dabei r1. Das Messinstrument sei am Anfang in einem (makroskopischen) Initialzustand, den man mit
eines Operators R ist, und der die zu messende Observable repräsentiert. Der entsprechende Messwert (Eigenwert) sei dabei r1. Das Messinstrument sei am Anfang in einem (makroskopischen) Initialzustand, den man mit 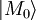 bezeichnet. Nachdem das Objekt die Wechselwirkung mit dem Messgerät durchlaufen hat befindet sich das Gerät in dem Zustand
bezeichnet. Nachdem das Objekt die Wechselwirkung mit dem Messgerät durchlaufen hat befindet sich das Gerät in dem Zustand 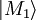 , der das Messergebnis r1 repräsentieren soll. Schematisch lässt sich dieser Vorgang folgendermaßen darstellen
, der das Messergebnis r1 repräsentieren soll. Schematisch lässt sich dieser Vorgang folgendermaßen darstellenDas Produkt der Zustände kann man vereinfacht als „und“ Verknüpfung verstehen. Formal entspricht es dem sogenannten Tensorprodukt der beiden Zustände.
Analog ist die Situation, wenn das Objekt am Anfang im Zustand
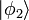 vorliegt. In diesem Fall ergibt die Wechselwirkung mit dem Messgerät das folgende Schema
vorliegt. In diesem Fall ergibt die Wechselwirkung mit dem Messgerät das folgende SchemaIst nun der Anfangszustand der gemessen werden soll kein Eigenzustand der zu messenden Observablen sondern eine Überlagerung von verschiedenen Eigenzuständen (Superposition), dann wird der Prozess der Messung komplizierter. Ist beispielsweise das Messobjekt am Anfang im Zustand
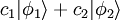 , so kann durch die Wechselwirkung mit dem Messgerät auch eine Superposition von Zuständen des Messgerätes resultieren, d. h. schematisch ergibt sich das Bild
, so kann durch die Wechselwirkung mit dem Messgerät auch eine Superposition von Zuständen des Messgerätes resultieren, d. h. schematisch ergibt sich das BildIn diesem Fall lässt sich der Zustand nach dem Durchlauf nicht mehr als Produkt faktorisieren und es ist dann nicht mehr offensichtlich, wie der Endzustand des Systems im Bezug auf das Messergebnis interpretiert werden sollte. Unterschiedliche Zustände des Messinstrumentes sind überlagert und das Messgerät befindet sich nicht in einem Eigenzustand. Lediglich nach der Registrierung des Objektes kann eine eindeutige Aussage gemacht werden, ob entweder
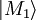 oder
oder 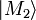 vorliegt. Die beiden Alternativen treten jeweils mit den Messwahrscheinlichkeiten | c1 | 2 bzw. | c2 | 2 auf.
vorliegt. Die beiden Alternativen treten jeweils mit den Messwahrscheinlichkeiten | c1 | 2 bzw. | c2 | 2 auf.Die Beschreibung der Wechselwirkung zwischen Objekt und Messgerät im Rahmen der Quantenmechanik kann somit einen Endzustand des Gesamtsystems ergeben, der keiner eindeutigen Zeigerstellung des Messgerätes entspricht. Andererseits werden am Messgerät in der Praxis eindeutige Ergebnisse abgelesen. Die Frage danach, auf welche Weise in diesem gesamten Prozess die Festlegung für den Endzustand des Gerätes geschieht, ist als Messproblem bekannt [3]. Der abrupte Übergang vom Zustand der Superposition zu einem der Eigenzustände wird in der Literatur manchmal als Kollaps der Wellenfunktion bezeichnet.
In diesem Zusammenhang geht die Kopenhagener Fassung der Quantenmechanik von der Grundannahme aus, dass die Messapparate grundsätzlich mit den Mitteln der klassischen Physik zu betrachten sind [4]. Gegen diese Sichtweise wird von manchen Physikern eingewendet, dass ungeklärt ist, wo genau der Übergang zwischen dem klassischen und dem quantenmechanischen Messgerät liegen soll. Eine Präzisierung dieser Fragestellung wird durch das Konzept der Zustandsreduktion erreicht.
Die Zustandsreduktion
Das von Neumann-Lüders-Projektionspostulat („Zustandspräparation“) macht eine Aussage darüber, wie der Zustandsvektor
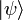 eines quantenmechanischen Systems durch eine Präparation verändert wird.[3][5]
eines quantenmechanischen Systems durch eine Präparation verändert wird.[3][5]- Projektionspostulat
- Ein Quantenobjekt im Zustand
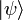 ist mit der Wahrscheinlichkeit
ist mit der Wahrscheinlichkeit 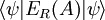 nach der Projektion auf eine Teilmenge A von möglichen Messergebnissen der Observablen
nach der Projektion auf eine Teilmenge A von möglichen Messergebnissen der Observablen 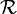 im Zustand
im Zustand
-
-
-
-
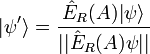 .
.
-
-
-
Der Zustandsvektor des Objektes wird dabei auf den vorgesehenen Teilbereich des Hilbertraums projiziert und anschließend normiert. Für einzelne Quantenobjekte kann man daher nicht mit Sicherheit sagen, ob sie nach der Projektion im (gewünschten) Zustand
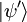 sein werden oder nicht. Die damit verbundene Unkenntnis macht den Unterschied zwischen Präparation und Informationsgewinn durch Messung deutlich. Präparationen werden daher häufig auf Teilchenstrahlen (Gesamtheiten) angewendet und die anschließende Messung ergibt Aufschluss über den Anteil der Gesamtheit, welcher die untersuchten Eigenschaften bei gegebener Präparation besitzt. Die Individualität der einzelnen Objekte bleibt dabei unberücksichtigt und auf eine Identifikation zwischen präpariertem- und registriertem Objekt muss verzichtet werden.
sein werden oder nicht. Die damit verbundene Unkenntnis macht den Unterschied zwischen Präparation und Informationsgewinn durch Messung deutlich. Präparationen werden daher häufig auf Teilchenstrahlen (Gesamtheiten) angewendet und die anschließende Messung ergibt Aufschluss über den Anteil der Gesamtheit, welcher die untersuchten Eigenschaften bei gegebener Präparation besitzt. Die Individualität der einzelnen Objekte bleibt dabei unberücksichtigt und auf eine Identifikation zwischen präpariertem- und registriertem Objekt muss verzichtet werden.Eine Besonderheit des Postulates ist, dass die Zustandsänderung diskontinuierlich und irreversibel ist und im Augenblick der Präparation stattfindet. Die abrupte Veränderung durch den Eingriff ist eine der Kernaussagen des quantenmechanischen Messprozesses. Es ist genau der Punkt, der aus metaphysisch-philosophischer Sicht den Bruch mit dem naiven Realismus fordert. Die Ablehnung des Realismus hat die Konsequenz, dass eine Observable im allgemeinen keinen bestimmten Wert hat, bevor er beobachtet wird (vgl. Bellsche Ungleichung). Dann heißt also, ihn messen, nicht, den Wert ermitteln den sie hat. In diesem Sinne bestimmt also der Messwert die Wirklichkeit und nicht umgekehrt. Heisenberg, Dirac und von Neumann verlangen als Messkriterium lediglich, dass bei Wiederholung einer Präparation am selben Objekt mit Sicherheit derselbe Zustand herauskommen muss. In diesem Fall ist also
-
-
-
-
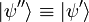 ,
,
-
-
-
was durch das Projektionspostulat respektiert wird. Für eine Teilchengesamtheit gilt demnach das gleiche.
Im Gegensatz dazu wird das „gewöhnliche“ deterministische Verhalten von Quantensystemen, wie beispielsweise die Wechselwirkung im Inneren eines Messgerätes, durch die kontinuierliche, reversible Zeitentwicklung der Schrödingergleichung beschrieben. Letztere ist daher grundsätzlich von der Zustandsänderung des Projektionspostulates zu unterscheiden.
Bedingte Wahrscheinlichkeiten
Eine quantitative Klassifikation von Messprozessen bezüglich mikroskopischer und makroskopischer Dimensionen lässt sich durch die Verwendung von Messwahrscheinlichkeiten vornehmen. Im Rahmen der Quantenmechanik bezieht sich die Messwahrscheinlichkeit immer auf eine vorgegebene Präparation des Messobjektes und ist daher als bedingte Wahrscheinlichkeit zu verstehen. Einen ersten Hinweis auf die Notwendigkeit von probabilistischen Ansätzen in Bezug auf die quantenmechanische Messung wurde von Popper bereits 1934 thematisiert.[6] Die grundlegende Bedeutung der bedingten Wahrscheinlichkeit für den quantenmechanischen Messprozess in der Kopenhagener Interpretation wurde zuerst von Friedman und Putnam 1978 herausgestellt.[7] Erwähnenswert ist insbesondere auch die Arbeit von Bub 1982.[8] Die Bedeutung von oberen Schranken für die bedingten Wahrscheinlichkeiten von Ort und Impuls, welche ein Abgrenzungskriterium zwischen klassischen und quantenmechanischen Messprozessen ermöglicht, wurden erst etwa 30 Jahre später erkannt und hergeleitet.[9]
Impulsmessungen
Ist ein Teilchen im Quantenzustand
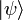 und beschreibt
und beschreibt 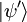 den Zustand des Objektes nach einer Präparation des Ortes x im Intervall A, dann gilt gemäß Projektionspostulat
den Zustand des Objektes nach einer Präparation des Ortes x im Intervall A, dann gilt gemäß Projektionspostulat-
-
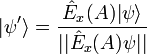 .
.
-
Dieser Zustand ist eine Superposition von unterschiedlichen Aufenthaltsorten im Intervall A und damit kein Eigenzustand des Ortsoperators. Wird bezüglich dieser Präparation eine Impulsmessung in x-Richtung vorgenommen, so ist die (bedingte) Messwahrscheinlichkeit für den Impuls p im Intervall B formal
-
-
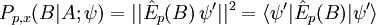 .
.
-
Die Indizes x und p auf der linken Seite der Gleichung bezeichnen darin, welche Observablen an dem Prozess beteiligt sind, – erst der Ort und dann der Impuls des Teilchens (von rechts nach links gelesen). Ersetzt man in der Formel auf der rechten Seite die Wellenfunktion gemäß des obigen Postulates, so ergibt sich der folgende allgemeine Ausdruck:
- Bedingte Wahrscheinlichkeit
-
-
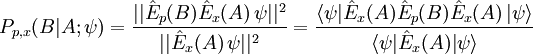 .
.
-
Die explizite Form der bedingten Wahrscheinlichkeit ist eine mathematische Konsequenz des Projektionspostulates für die Zustandsreduktion und der formalen Regeln der Quantentheorie.
Die gewöhnliche Wahrscheinlichkeit für eine Impulsmessung ergibt sich aus dem Spezialfall, indem die Menge A keiner Einschränkung unterliegt und somit der gesamten reellen Achse entspricht, mit dem Ergebnis (vgl. Born):
-
-
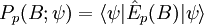 .
.
-
Werden hingegen für die beiden Ereignismengen A und B endliche Orts- bzw. Impulsintervalle
![[\scriptstyle -\frac{\Delta x}{2},\frac{\Delta x}{2}\textstyle]](/pictures/dewiki/57/9a088eb4cdd830f00a3cfdb09580fe2e.png) und
und ![[\scriptstyle -\frac{\Delta p}{2},\frac{\Delta p}{2}\textstyle]](/pictures/dewiki/102/f778a67fced2c5c86c94623c3b5b1b86.png) betrachtet, so ergibt sich ein davon sehr unterschiedliches Bild:
betrachtet, so ergibt sich ein davon sehr unterschiedliches Bild:- Obere Schranke für Impulsmessungen
Wird eine Präparation des Ortes mit einer endlichen Genauigkeit Δx > 0 vorgenommen, so lässt sich über die Messwahrscheinlichkeit für den Impuls die folgende Ungleichung angeben[9]
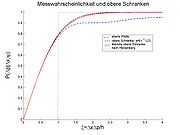
wobei „erf“ die Gaußsche Fehlerfunktion bezeichnet. Die Ungleichung hat Gültigkeit für jeden beliebigen Zustandsvektor ψ und stellt daher ein allgemeines Klassifikationskriterium für die Messwahrscheinlichkeit dar. Gemäß dieser Ungleichung ist eine beliebig genaue Impulsmessung zwar immer noch möglich, jedoch ist die Wahrscheinlichkeit für solche Messereignisse nach oben beschränkt (Abb.1). Je nach Wahl der Intervalle Δx und Δp ist die Schranke beliebig klein.
Die in Abbildung 1 dargestellten oberen Schranken zeigen einen stetigen und monoton steigenden Übergang zwischen mikroskopischen (
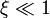 ) und makroskopischen (
) und makroskopischen (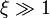 ) Messbereichen. Ein abrupter Übergang ist nicht vorhanden. Eine solche Form der Klassifikation präzisiert die Vorstellung der Kopenhagener Schule dahingehend, inwiefern ein Messprozess (= Präparation und Registrierung) auf mikroskopischen Skalen für Messungen noch geeignet ist oder seine Bedeutung als Messgerät verliert. Experimentelle Prüfung der oberen Schranke lassen sich problemlos mit Laserexperimenten durchführen.[10]
) Messbereichen. Ein abrupter Übergang ist nicht vorhanden. Eine solche Form der Klassifikation präzisiert die Vorstellung der Kopenhagener Schule dahingehend, inwiefern ein Messprozess (= Präparation und Registrierung) auf mikroskopischen Skalen für Messungen noch geeignet ist oder seine Bedeutung als Messgerät verliert. Experimentelle Prüfung der oberen Schranke lassen sich problemlos mit Laserexperimenten durchführen.[10]Der prinzipielle Unterschied zwischen einem klassischen- und einem quantenmechanischen Messprozess lässt sich somit formal durch die folgenden beiden Grenzwerte präzisieren:
für alle Δx > 0. Der zweite Grenzwert kann in der Natur jedoch nicht beobachtet werden. Ein Realisierung für den quantenmechanischen Grenzwert ergibt das Beispiel im folgenden Kapitel.
Einfachspaltexperiment
Man betrachte eine ebenen Welle, die von links auf einen Spalt der Breite Δx trifft (vgl. Abb. 2). Die Präparation des Teilchens geschieht durch den Spalt, der die gewünschten Teilchenbahnen passieren lässt. Durch Fouriertransformation des neuen Zustands erhält man die Wahrscheinlichkeitsdichte für den Impuls.
Wird dieser Vorgang für eine Teilchengesamtheit durchgeführt, so ergibt sich die Wahrscheinlichkeit dafür, einen Impuls im Intervall Δp zu messen, durch
Die Berechnung dieses Integrals ergibt
In dieser Formel ist Si(x) das sog. sine-integral und
ein Parameter mit der Einheit 1. Die bedingte Wahrscheinlichkeit für die Impulsmessung ist in diesem Experiment ausschließlich von dem Produkt des Präparationsparameters Δx und der gewählten Messgenauigkeit Δp abhängig und diesbezüglich streng monoton steigend. Wählt man beispielsweise eine Messanordnung mit Parametern aus, die der Bedingung ΔxΔp = h genügen, so wird dieser Messprozess nur mit einer Wahrscheinlichkeit von
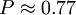 erfolgreich Impulse registrieren können, da die Impulsmessung grundsätzlich durch die vorhergehende Präparation des Ortes beeinflusst wird (vgl. Abb.1).
erfolgreich Impulse registrieren können, da die Impulsmessung grundsätzlich durch die vorhergehende Präparation des Ortes beeinflusst wird (vgl. Abb.1).Doppelspaltexperiment
Beim Messprozess im Doppelspaltexperiment trifft das Quantenobjekt zunächst auf zwei parallele, schmale Spalte bevor es auf dem dahinterliegenden Schirm registriert wird. Dabei stellt sich die Frage, welches Intensitätsmuster auf dem Schirm erscheint. Im klassischen Teilchenbild wird unterstellt, dass ein Messobjekt entweder durch den oberen Spalt (z. B. A1) oder durch den unteren Spalt (A2) auf den Schirm gelangt, aber nie durch beide Spalte gleichzeitig. Diese (klassische) Vorstellung würde für ein Ereignis B auf dem Schirm gemäß der Bayes-Regel für die totale Wahrscheinlichkeit formal den Ausdruck
ergeben. Dieser Ansatz wird im Experiment jedoch nicht gemessen. Daher kann nicht grundsätzlich davon ausgegangen werden, dass die Quantenobjekte nur jeweils einen Spalt durchlaufen.
Die richtige Beschreibung ergibt sich hingegen, wenn die ψ-Funktion des Quantenobjektes zu Beginn eine Zustandsreduktion durch den gesamten Doppelspalt gemäß des Projektionspostulats erfährt. Die entsprechende Wahrscheinlichkeit für das Ereigniss B auf dem Schirm ergibt sich dann aus
Dieses Ergebnis gilt auch dann, wenn die Intensität des einfallenden Teilchenstrahls so gering ist, dass von einer Interferenz der Objekte untereinander hinter dem Doppelspalt abgesehen werden kann. Bemerkenswert ist zudem, dass die Registrierungen auf dem Schirm einen Teilchencharakter der Objekte nahelegen.
Ortsmessungen
Die Behandlung von zwei nacheinander ausgeführten Ortsmessungen unterscheidet sich grundsätzlich von der Betrachtung der Orts- und Impulsmessung. Beschreibt beispielsweise
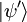 den Zustand eines Quantenobjektes nach einer Präparation des Ortes
den Zustand eines Quantenobjektes nach einer Präparation des Ortes 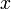 , dann gilt gemäß Postulat
, dann gilt gemäß Postulat-
-
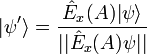 .
.
-
Eine unmittelbar im Anschluss daran folgende Ortsmessung dieser Art würde daher denselben Zustand
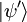 ergeben. Vergeht andererseits nach der ersten Messung eine endliche Zeit t > 0, so wird sich der Zustand
ergeben. Vergeht andererseits nach der ersten Messung eine endliche Zeit t > 0, so wird sich der Zustand 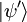 entsprechend der Schrödingergleichung zeitlich entwickeln. Eine solche Zeitentwicklung wird formal durch den sogenannten Zeitentwicklungsoperator
entsprechend der Schrödingergleichung zeitlich entwickeln. Eine solche Zeitentwicklung wird formal durch den sogenannten Zeitentwicklungsoperator 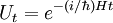 dargestellt. Verstreicht nach der ersten Ortsmessung also die Zeit t, so ergibt sich der folgende Zustand
dargestellt. Verstreicht nach der ersten Ortsmessung also die Zeit t, so ergibt sich der folgende Zustand-
-
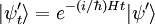 ,
,
-
wobei H der Hamiltonoperator des Teilchens ist.
Ist nun B ein weiteres Ortsintervall auf der reellen Achse, so erhält man nach der Zeit t die Wahrscheinlichkeit einen Ort aus B zu messen durch
-
-
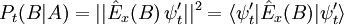 .
.
-
Der Index t repräsentiert dabei die zeitliche Entwicklung zwischen den beiden Ortsmessungen. Nach Resubstitution der Zustandsfunktion ergibt sich schließlich der allgemeine Ausdruck für die bedingte Wahrscheinlichkeit von zwei aufeinanderfolgenden Ortsmessungen im zeitlichen Abstand t
-
-
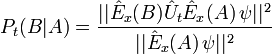 .
.
-
Für den Spezialfall t = 0 ergibt sich eine Wahrscheinlichkeit von 1, falls A eine Teilmenge von B ist. Hingegen ist für endliche Zeitintervalle, t > 0, die Wahrscheinlichkeit in jedem Fall echt kleiner als 1.
- Obere Schranke für Ortsmessungen
Man wähle für die Mengen A und B jeweils die endlichen Intervalle der Länge Δx und Δx'. Dann entspricht Pt(Δx' | Δx) der Wahrscheinlichkeit dafür, dass ein Teilchen nach der Zeit t im Intervall Δx' gefunden wird, wenn es zu Beginn im Intervall Δx präpariert wurde. Generell ist diese Wahrscheinlichkeit abhängig vom individuellen Quantenzustand des betrachteten Messobjektes. Im Rahmen der Spektraltheorie linearer Operatoren lässt sich jedoch eine obere Schranke für die bedingte Wahrscheinlichkeit bestimmen, welche unabhängig vom Teilchenzustand ist. Formal ergibt sich die allgemeingültige Ungleichung[9]
wobei
ein dimensionsloser Parameter ist und m die Masse des Teilchens bezeichnet. Die „erf“-Funktion ist monoton steigend, kleiner als 1 und erf(0) = 0. Für große Massen strebt die rechte Seite der Ungleichung gegen den Wert 1 und es ergibt sich der klassische Grenzfall. Für kleine Massen hingegen wird eine erfolgreiche Registrierung des Objektes immer unwahrscheinlicher.
- Beispiel
Wählt man für ein Elektron die Messgenauigkeiten Δx' = Δx = 2 Millimeter und einen zeitlichen Abstand von t = 10 Millisekunden, so kann die Wahrscheinlichkeit dafür, das Objekt im Intervall Δx' zu finden, nicht größer als 0.51 sein.
Eine allgemeine kleinste obere Schranke für die bedingte Wahrscheinlichkeit Pt(Δx' | Δx) ist ebenfalls berechenbar. Sie steht im direkten Zusammenhang mit einer speziellen Klasse von Funktionen, den sogenannten Sphäroidfunktionen[9].
Spinmessungen
Für eine Spinmessung ist es zunächst notwendig eine Richtung vorzugeben in welcher der Spin gemessen werden soll. Dazu betrachtet man beispielsweise einen Einheitsvektor
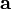 im Ortsraum. Die eigentliche Spinmessung wird dann mit Hilfe des Vektors
im Ortsraum. Die eigentliche Spinmessung wird dann mit Hilfe des Vektors 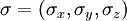 der Pauli-Matrizen ermöglicht. Der dazugehörige Operator ist durch das Skalarprodukt von
der Pauli-Matrizen ermöglicht. Der dazugehörige Operator ist durch das Skalarprodukt von 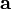 mit dem Spin-Vektor gegeben
mit dem Spin-Vektor gegebenDas zu diesem Operator gehörige Eigenwertproblem ist
d. h., die Eigenwerte des Operators sind
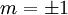 und repräsentieren die beiden Spinrichtungen „up“ und „down“ bezüglich der Orientierung des Vektors
und repräsentieren die beiden Spinrichtungen „up“ und „down“ bezüglich der Orientierung des Vektors 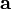 . Mit Hilfe der darin enthaltenen Eigenvektoren lässt sich der folgende Spin-Projektor konstruieren
. Mit Hilfe der darin enthaltenen Eigenvektoren lässt sich der folgende Spin-Projektor konstruierenWie jeder Projektor hat dieser Operator gemäß Definition die Eigenschaft der Idempotenz, d. h. es gilt:
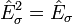 . Daher sind seine Eigenwerte „1“ und „0“. Letztere werden in der Quantenlogik manchmal als „Ja/Nein“-Aussagen interpretiert.
. Daher sind seine Eigenwerte „1“ und „0“. Letztere werden in der Quantenlogik manchmal als „Ja/Nein“-Aussagen interpretiert.Bedingte Wahrscheinlichkeit bei Spinmessung
Man betrachtet nun ein Ensemble von Teilchen in einem beliebigen Quantenzustand ψ. Eine Auswahl (Selektion) derjenigen Teilchen aus diesem Ensemble, welche der vorgegebenen Projektion
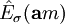 in Richtung des Vektors
in Richtung des Vektors 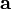 entsprechen, ergibt gemäß dem Projektionspostulat den normierten Quantenzustand
entsprechen, ergibt gemäß dem Projektionspostulat den normierten Quantenzustand-
-
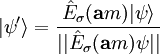 .
.
-
Dieser Zustand ergibt sich bei jedem Einzelexperiment mit einer Wahrscheinlichkeit von
-
-
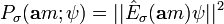 .
.
-
Wird am präparierten Zustand ψ' eine Spin-Messung in Richtung eines zweiten Vektors
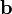 vorgenommen, dann ist die Wahrscheinlichkeit dafür, ein Teilchen mit einer Spinorientierung in dieser Richtung vorzufinden (Registrierung) gleich
vorgenommen, dann ist die Wahrscheinlichkeit dafür, ein Teilchen mit einer Spinorientierung in dieser Richtung vorzufinden (Registrierung) gleich-
-
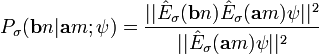 .
.
-
Nach Substitution der entsprechenden Projektoren ergibt sich der von ψ unabhängige Ausdruck
Der Einfachheit halber beschränkt man sich (z. B. in Experimenten) häufig auf Richtungsvektoren
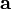 und
und 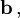 die beide in der x-z-Ebene des Ortsraumes liegen und deren Orientierung in beiden Fällen auf die z-Achse bezogen wird. Man bezeichnet die entsprechenden Winkel mit
die beide in der x-z-Ebene des Ortsraumes liegen und deren Orientierung in beiden Fällen auf die z-Achse bezogen wird. Man bezeichnet die entsprechenden Winkel mit 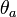 und
und 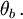 (Dabei beachte man den Unterschied zum Zwei-Teilchen-System, welches weiter unten behandelt wird. Werden hier zwei aufeinander folgende Beobachtungen an einem Objekt vorgenommen, so wird dort jeweils eine Beobachtung an zwei verschiedenen Objekten durchgeführt.)
(Dabei beachte man den Unterschied zum Zwei-Teilchen-System, welches weiter unten behandelt wird. Werden hier zwei aufeinander folgende Beobachtungen an einem Objekt vorgenommen, so wird dort jeweils eine Beobachtung an zwei verschiedenen Objekten durchgeführt.)Für die bedingte Wahrscheinlichkeit von Messungen mit den angegebenen Orientierungen vereinfacht sich die vorige Gleichung zu
Häufig wird diese Formel auch in einer äquivalenten Form angegeben
-
-
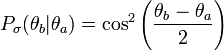 .
.
-
Diese Formel für die bedingte Wahrscheinlichkeit spielt u. a. eine wichtige Rolle im Zusammenhang mit der Bell’schen Ungleichung und der Herleitung des Quanten-Zeno-Effektes.
Häufig wiederholte Spinmessungen
Quantenmechanische Messungen greifen in die dynamische Entwicklung eines Quantensystems ein und führen zu wesentlichen Veränderungen. Als Beispiel betrachte man ein Teilchen dessen Spin zu Beginn im Zustand ψ präpariert wurde. Es werden dann über eine Zeit T hin N Selektionen vorgenommen, die ausgehend von der Orientierung θa = 0 jeweils um den Winkel
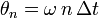 und
und 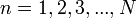 in Richtung der x-Achse gedreht sind. Der letzte Winkel am Ende dieses Durchlaufs ist
in Richtung der x-Achse gedreht sind. Der letzte Winkel am Ende dieses Durchlaufs ist 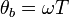 . Die Wahrscheinlichkeit für einen erfolgreichen Durchlauf eines Teilchens durch N solcher Selektionen ist
. Die Wahrscheinlichkeit für einen erfolgreichen Durchlauf eines Teilchens durch N solcher Selektionen ist-
-
![P(N)= \prod\limits_{n=1}^N P_\sigma(\theta_n|\theta_{n-1})=
\left[\frac{1}{2}\,\left(1+\cos(\frac{\omega T}{N})\right)\right]^N](/pictures/dewiki/57/9212b507ed6035db3228bf90eb5601c4.png) ,
,
-
wobei für den Anfangszustand eine Orientierung in die positive z-Richtung verwendet wurde. Für eine sehr große Anzahl N von zwischenzeitlichen Selektionen ergibt sich das Grenzverhalten
-
-
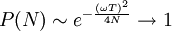 .
.
-
Dem System ist daher eine vorgegebene Zustandsbewegung durch eine Sequenz entsprechender projektiver Messungen durch den Experimentator aufgezwungen worden. Dieses Phänomen wird in der Literatur als Quanten-Zeno-Effekt bezeichnet[11].
Spin-Messungen an zusammengesetzten Systemen
Von der klassischen Physik her ist man gewohnt, dass zusammengesetzte Systeme in Teilsysteme oder Untersysteme zerlegt werden können. In der Quantenmechanik zeigt sich, dass zusammengesetzte Systeme darüber hinaus völlig andere und überraschende ganzheitliche Eigenschaften aufweisen können. Sie treten auf, wenn sich zusammengesetzte Quantensysteme in verschränkten Zuständen befinden.
Es können z. B. Quantensysteme präpariert werden, bei denen man an zwei verschiedenen Orten bei Messungen jeweils ein Photon registriert. Analoge Systeme gibt es auch für Elektronen. Zwei solche Teilchen werden als nicht unterscheidbar angesehen. Unterscheidbar sind hingegen die Orte der Objekte, an denen bei einer Messung z. B. eine Photonenpolarisation gemessen wird.
Formal kann man z. B. zwei unabhängige Quantensysteme S1 und S2 betrachten, die jeweils durch die Spin-Zustände
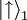 und
und 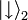 dargestellt werden. Die Pfeile werden in der Literatur häufig verwendet, wenn die jeweiligen Spins in z-Richtung („up“ bzw. „down“) präpariert sind. Das Produkt
dargestellt werden. Die Pfeile werden in der Literatur häufig verwendet, wenn die jeweiligen Spins in z-Richtung („up“ bzw. „down“) präpariert sind. Das Produktdefiniert ein aus den beiden Teilsystemen gebildetes Gesamtsystem, d. h. einen Produktzustand der Teilchen. In diesem speziellen Fall faktorisiert die Zweiteilchenwellenfunktion und es handelt sich um unabhängige Teilsysteme, da keine Abhängigkeit zwischen den Systemen nachgewiesen werden kann.
Eine Verschränkung der Teilsysteme ergibt sich u. a. für den sog. Singulettzustand, der im Rahmen des EPR-Gedankenexperimentes eine zentrale Rolle spielt.[12] Die formale Darstellung dieses Zustandes ist
-
-
![\left|\phi\right\rangle=\frac{1}{\sqrt{2}}\,\Big[\,\left|\uparrow\downarrow\right\rangle-\left|\downarrow\uparrow\right\rangle\Big]](/pictures/dewiki/99/c7ede1cd8d777b7d5089bb0daa225ebd.png) .
.
-
Dieser Zustand lässt sich nicht als ein Produkt der zwei Einteilchenzustände darstellen. Eine Messung der einzelnen Spins der beiden Teilchen in z-Richtung ergibt mit Wahrscheinlichkeit 1 entgegengesetzte Vorzeichen und ist unabhängig von der Reihenfolge mit welcher die Messungen an den beiden Komponenten durchgeführt werden. Die Festlegung auf die Orientierung in z-Richtung ist keine Beschränkung der Allgemeinheit, da dieser Zustand die Eigenschaft der Rotationsinvarianz besitzt.
Im Rahmen des EPR-Experimentes werden für zwei fest vorgegebene Richtungsvektoren a und b, Spinmessungen an den beiden Komponenten 1 und 2 des Singulettzustandes durchgeführt. Dabei kann man nach der bedingten Wahrscheinlichkeit fragen, bei Teilchen 2 einen Spin
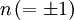 in b-Richtung zu erhalten, wenn die Messung an Teilchen 1 das Ergebnis
in b-Richtung zu erhalten, wenn die Messung an Teilchen 1 das Ergebnis 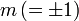 in a-Richtung ergeben hat:
in a-Richtung ergeben hat:-
-
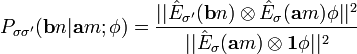 .
.
-
Das Tensorprodukt der Operatoren macht deutlich, das der jeweils links in diesem Produkt vorkommende Operator nur auf die erste Komponente des Singuletzustandes angewendet wird, während der jeweils rechts stehende Operator nur auf die zweite Komponente des Singulattzustandes angewendet werden soll. Der Nenner ist gleich der Wahrscheinlichkeit
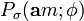 , bei einer Spinmessung am Teilchen 1 in a-Richtung den Wert m zu erhalten. Man beachte dabei, dass diese Wahrscheinlichkeit immer gleich 1/2 ist unabhängig davon, in welche Richtung a bei der Messung hat. Der 1-Operator im Nenner bedeutet, dass die zweite Komponente des Singuletzustandes bei der Erwartungswertbildung unverändert bleibt.
, bei einer Spinmessung am Teilchen 1 in a-Richtung den Wert m zu erhalten. Man beachte dabei, dass diese Wahrscheinlichkeit immer gleich 1/2 ist unabhängig davon, in welche Richtung a bei der Messung hat. Der 1-Operator im Nenner bedeutet, dass die zweite Komponente des Singuletzustandes bei der Erwartungswertbildung unverändert bleibt.Nach den Regeln der Spin-Algebra ergibt sich für die bedingte Wahrscheinlichkeit das formal einfache Ergebnis
-
-
![P_{\sigma,\sigma'}(n|m;\theta_a,\theta_b)=\frac{1}{2}\left[1-n\,m\,\cos(\theta_b-\theta_a)\right]](/pictures/dewiki/53/53b6f931cdbdf2483c3ef386f147b8e7.png) ,
,
-
wobei m und n jeweils die Werte +1 („up“) oder −1 („down“) haben kann. Diese Wahrscheinlichkeit ist invariant gegenüber der Vertauschung der Winkel und der beiden Spins.
Die Verbundwahrscheinlichkeit der beiden Ereignisse ist gleich dem Produkt aus der bedingten Wahrscheinlichkeit und der Randwahrscheinlichkeit, d. h.
-
-
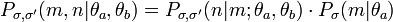 .
.
-
Damit lässt sich die Korrelation
![\text{E}\left[\mathbf{a},\mathbf{b}\right]](/pictures/dewiki/52/4412c7f68f785d54d467002bbbdca480.png) der beiden Spin-Operatoren durch gewöhnliche Erwartungswertbildung über die Zufallsvariablen der beiden Spin-Parameter berechnen:
der beiden Spin-Operatoren durch gewöhnliche Erwartungswertbildung über die Zufallsvariablen der beiden Spin-Parameter berechnen:wobei der letzte Term das gewöhnliche Skalarprodukt der beiden Richtungsvektoren darstellt. Der spezielle Fall gleicher Orientierungen der beiden Messrichtungen a und b entspricht einer Winkeldifferenz von 0°. In diesem Fall ist die Korrelation gleich −1. Bilden hingegen die Messorientierungen einen relativen Winkel von 90°, d. h. sie sind orthogonal zueinander ausgerichtet, dann ergibt die obige Formel eine verschwindende Korrelation von 0.
Einzelnachweise
- ↑ W. Heisenberg: Physik und Philosophie. Hirzel, Stuttgart 1959.
- ↑ W.E. Lamb, An Operational Interpretation of nonrelativistic Quantum Mechanics, Physics Today 22 (1969) Heft 4, 23–28.
- ↑ a b c J. v. Neumann, Mathematische Grundlagen der Quantenmechanik, Springer (1932, 1968, 1996).
- ↑ N. Bohr: The Quantum Postulate and the Recent Development in Atomic Theory. In: Nature 121, Nr. 78, 1928, S. 580–590. (Vortrag auf dem Internationalen Physikerkongress in Como 1927). Deutsche Fassung in: Die Naturwissenschaften 16, 1928, S. 245–257.
- ↑ G. Lüders, Über die Zustandsänderung durch den Messprozess, Ann. Phys. (Leipzig), 8 (1951) 322–328. online
- ↑ K. Popper: Logik der Forschung. 10. Auflage, Tübingen 1994/1934.
- ↑ M. Friedman und H. Putnam, Quantum Logic, Conditional Probability, and Interference, Dialectica 32 (1978), 305–315.
- ↑ J. Bub, Quantum Logic, Conditional Probability, and Interference, Philosophy of Science 49 (1982), 402–421 online.
- ↑ a b c d T. Schürmann, A Single Particle Uncertainty Relation. In: Acta Physica Polonica B. Vol 39 (2008) 587–597, online.
- ↑ W. Görlich, I. Hoffmann, T. Schürmann: Experimental test of the Heisenberg uncertainty relation for position and momentum. In: arXiv. Quantum Physics. 2008 (arXiv:0812.4775).
- ↑ B. Misra and E.C.G. Sudarshan, The Zeno’s paradox in quantum theory, J. Math. Phys. 18, 756–763 (1977).
- ↑ „Verschränkt“ wäre auch der analoge „Triplett“-Zustand, der sich vom Singulettzustand durch ein Plus anstelle des Minus-Zeichens unterscheidet. Nicht-verschränkt wären dagegen die beiden andern Triplett-Zustände,
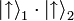 und
und 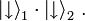
Literatur
- Erhard Scheibe: Die Philosophie der Physiker. Verlag C. H. Beck, München 2006. (Kap. VIII, S. 261 ff).
- John v. Neumann, Mathematische Grundlagen der Quantenmechanik, [Nachdr. der Ausg.] Berlin, Springer, 1932. – Berlin; Heidelberg; New York: Springer, 1996.
- Stanley P. Gudder, Quantum Probability, Academic Press, Inc. 1988. (Kap. 2.3.).
Siehe auch
Wikimedia Foundation.

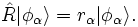
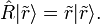
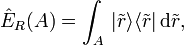
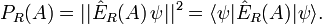
![P_x([a,b]) = \int_{[a,b]} \,\langle \psi|x\rangle\langle x|\psi\rangle \,dx
=\int_{a}^b|\psi(x)|^2\,dx,](/pictures/dewiki/55/78b6b5269f5132f314205197b22d9935.png)
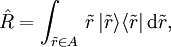
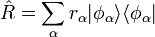
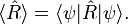
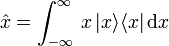
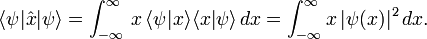
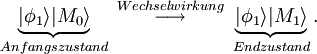
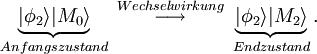
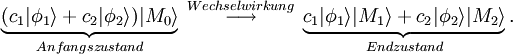
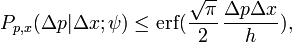
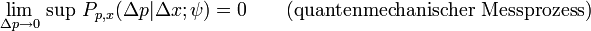
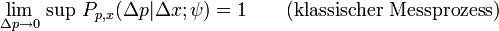
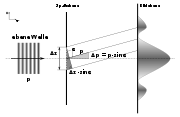
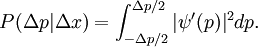
![P(\Delta p|\Delta x) = \frac{2}{\pi}\left[\text{Si}(\pi\xi)-\frac{2}{\pi}\frac{\sin(\frac{\pi\xi}{2})^2}{\xi}\right].](/pictures/dewiki/97/a88604f54da1163f4f525b1b3c1afa7d.png)
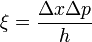
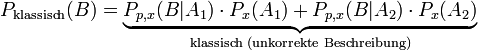

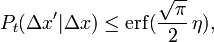
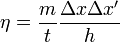
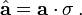
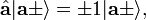
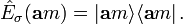
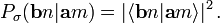
![P_\sigma(\theta_b|\theta_a)=\frac{1}{2}\,\left[1+\cos(\theta_b-\theta_a)\right]\,.](/pictures/dewiki/97/a9e702775e7e5b0913fe140117784f42.png)
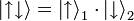
![\text{E}\left[\mathbf{a},\mathbf{b}\right]:=\langle\phi|\hat\mathbf{a}\otimes\hat\mathbf{b}|\phi\rangle=\sum_{m,n=\pm 1}\,n\,m\,P_{\sigma,\sigma'}(m,n|\theta_a,\theta_b)=-\cos(\theta_b-\theta_a)=-\,\mathbf{a}\cdot\mathbf{b},](/pictures/dewiki/54/6dd584032de0bc973806d76fd9794a4f.png)