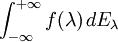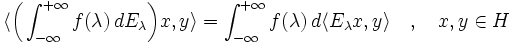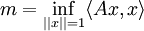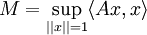- Spektralschar
-
In der Mathematik, insbesondere in der Funktionalanalysis ist ein Spektralmaß eine Abbildung, die gewissen Teilmengen einer fest gewählten Menge orthogonale Projektionen eines Hilbertraumes zuordnet. Spektralmaße werden verwendet um Ergebnisse in der Spektraltheorie linearer Operatoren zu formulieren, wie z. B. den Spektralsatz für normale Operatoren. Daneben wird der Begriff, jedoch mit anderer Bedeutung, in der Stochastik verwendet.
Definition
Es seien
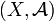 ein Messraum, H ein reeller bzw. komplexer Hilbertraum, L(H) der Banachraum der stetigen linearen Operatoren auf H und P(H) die Menge der orthogonalen Projektoren von H.
ein Messraum, H ein reeller bzw. komplexer Hilbertraum, L(H) der Banachraum der stetigen linearen Operatoren auf H und P(H) die Menge der orthogonalen Projektoren von H.Definition: Ein Spektralmaß für das Tripel
 ist eine Abbildung
ist eine Abbildung  mit den folgenden Eigenschaften:
mit den folgenden Eigenschaften:- Es gilt
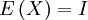 . Dabei ist
. Dabei ist  die Identität auf H.
die Identität auf H. - Für jedes
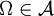 ist
ist 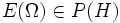 , d. h. E ist Projektor-wertig.
, d. h. E ist Projektor-wertig. - Für alle
 ist
ist 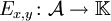 mit
mit 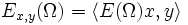 ein komplexes bzw. signiertes Maß auf
ein komplexes bzw. signiertes Maß auf 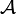 .
.
Das Quadrupel
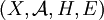 heißt ein Spektralmaßraum.
heißt ein Spektralmaßraum.Häufig wird die auf diese Weise definierte Abbildung E auch als Zerlegung der Einheit I (engl.: resolution of identity) bezeichnet. Auch ist es üblich von einem Projektor-wertigen Maß (engl.: projection-valued measure, häufig kurz PVM) zu sprechen.
Ist X ein topologischer Raum,
 seine Topologie und
seine Topologie und 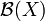 seine Borelalgebra, so heißt ein Spektralmaß E, dem der Borelsche Messraum
seine Borelalgebra, so heißt ein Spektralmaß E, dem der Borelsche Messraum 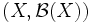 zugrundeliegt, ein Borelsches Spektralmaß. Ist speziell
zugrundeliegt, ein Borelsches Spektralmaß. Ist speziell 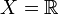 bzw.
bzw. 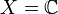 , so heißt das Borelsches Spektralmaß ein reelles bzw. komplexes Spektralmaß. Der Träger eines Borelschen Spektralmaßes ist als
, so heißt das Borelsches Spektralmaß ein reelles bzw. komplexes Spektralmaß. Der Träger eines Borelschen Spektralmaßes ist alsdefiniert. Dies ist das Komplement der größten offenen Teilmenge G von X, für die E(G) = 0 ist.
Eigenschaften
Es sei E ein Spektralmaß für das Datum
 . Dann gelten die folgenden Aussagen:
. Dann gelten die folgenden Aussagen: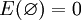
- Modularität: Es gilt
 für alle
für alle  .
. - Multipikativität: Es gilt
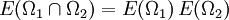 für alle
für alle  . Insbesondere kommutieren die Projektoren E(Ω1) und E(Ω2) miteinander und das Bild von E(Ω1) ist senkrecht zum Bild von E(Ω2), wenn
. Insbesondere kommutieren die Projektoren E(Ω1) und E(Ω2) miteinander und das Bild von E(Ω1) ist senkrecht zum Bild von E(Ω2), wenn 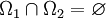 gilt.
gilt.
Insbesondere ist jedes Spektralmaß ein endlich additives vektorielles Maß.
Setzt man Ex: = Ex,x für
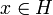 , so gilt für alle
, so gilt für alle  aufgrund der Polarizationsgleichung
aufgrund der Polarizationsgleichungim komplexen Fall bzw.
im reellen Fall. Insbesondere sind die Maße Ex,y bekannt, wenn die Maße Ex bekannt sind, so dass man häufig nur mit diesen arbeitet.
Äquivalente Definition
Häufig findet man die folgende Charakterisierung von Spektralmaßen in der Literatur als Definition. Eine Abbildung
 ist genau dann ein Spektralmaß, wenn
ist genau dann ein Spektralmaß, wenn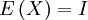 gilt,
gilt,- E Projektor-wertig ist und
- für jede Folge
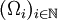 von
von 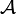 -messbaren, paarweise disjunkten Mengen :
im Sinne der starken Operatortopologie gilt. Diese Eigenschaft wird gelegentlich als punktweise σ-Additivität bezeichnet.
-messbaren, paarweise disjunkten Mengen :
im Sinne der starken Operatortopologie gilt. Diese Eigenschaft wird gelegentlich als punktweise σ-Additivität bezeichnet.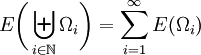
Die Bezeichnung Zerlegung der Einheit für E lässt sich nun wie folgt erklären. Ist
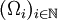 eine abzählbare Zerlegung von X in
eine abzählbare Zerlegung von X in 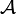 -messbare Mengen, so gilt
-messbare Mengen, so giltbzw.
wobei
 die orthogonale Summe im Sinne von Hilberträumen der Familie
die orthogonale Summe im Sinne von Hilberträumen der Familie 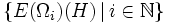 von abgeschlossenen Unterräumen ist. Dies entspricht der Tatsache, dass die Eigenräume eines normalen Operators des
von abgeschlossenen Unterräumen ist. Dies entspricht der Tatsache, dass die Eigenräume eines normalen Operators des 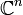 eine orthogonale Summenzerlegung von
eine orthogonale Summenzerlegung von 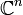 bilden.
bilden.Beispiele
- Es sei
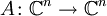 ein normaler linearer Operator. Dann ist das Spektrum von A nicht leer und besteht aus den Eigenwerten von A. Die Eigenräume zu den paarweise verschiedenen Eigenwerten von A stehen paarweise senkrecht aufeinander und besitzen
ein normaler linearer Operator. Dann ist das Spektrum von A nicht leer und besteht aus den Eigenwerten von A. Die Eigenräume zu den paarweise verschiedenen Eigenwerten von A stehen paarweise senkrecht aufeinander und besitzen 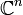 als (innere) direkte Summe. Dies ist äquivalent dazu, dass :
gilt. Dabei ist Pλ die orthogonale Projektion von
als (innere) direkte Summe. Dies ist äquivalent dazu, dass :
gilt. Dabei ist Pλ die orthogonale Projektion von
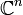 auf den Eigenraum von A zum Eigenwert λ. Aus dieser Darstellung von
auf den Eigenraum von A zum Eigenwert λ. Aus dieser Darstellung von 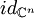 erhält man die folgende "Spektralauflösung" von A:
Das Spektralmaß von A ist:
erhält man die folgende "Spektralauflösung" von A:
Das Spektralmaß von A ist: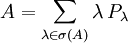 Ist A ein beliebiger normaler Operator, so kann das Spektrum von A kontinuierlich sein oder sich in einem Punkt häufen und man ersetzt obige Summe durch einen kontinuierlichen Summationsbegriff, nämlich durch ein (Operator-wertiges) Integral.
Ist A ein beliebiger normaler Operator, so kann das Spektrum von A kontinuierlich sein oder sich in einem Punkt häufen und man ersetzt obige Summe durch einen kontinuierlichen Summationsbegriff, nämlich durch ein (Operator-wertiges) Integral.
- Jeder normaler Operator A eines Hilbertraumes bestimmt ein Spektralmaß. Nach dem Spektralsatz für normale Operatoren ist der Operator A eindeutig durch dieses Spektralmaß beschrieben.
- Es sei L2[0,1] der Hilbertraum der im Lebesguesche Sinne quadrat-summierbaren Funktionen auf dem Einheitsintervall [0,1] und
![\mathcal{B}[0,1]](/pictures/dewiki/55/77a065cd84477fefc0f7cd9ce61f760c.png) die Borelalgebra von [0,1]. Für eine wesentlich beschränkte Funktion f auf [0,1] bezeichne Mf den durch Multiplikation mit f induzierten Operator auf L2[0,1]. Setzt man
die Borelalgebra von [0,1]. Für eine wesentlich beschränkte Funktion f auf [0,1] bezeichne Mf den durch Multiplikation mit f induzierten Operator auf L2[0,1]. Setzt man 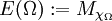 für eine Borelmenge Ω des Einheitsintervalls, so wird hierdurch ein Spektralmaß E für das Datum
für eine Borelmenge Ω des Einheitsintervalls, so wird hierdurch ein Spektralmaß E für das Datum ![([0,1],\mathcal{B}([0,1]),L^2[0,1])](/pictures/dewiki/55/7b4d920498b3d3b03391fca1fb6790de.png) definiert. Dieses Spektralmaß ist das Spektralmaß des Multiplikationsoperators Mid.
definiert. Dieses Spektralmaß ist das Spektralmaß des Multiplikationsoperators Mid.
Integration bezüglich eines Spektralmaßes
Es sei
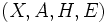 ein Spektralmaßraum. Mithilfe der zu E assoziierten komplexen Maße Ex,y kann man für gewisse
ein Spektralmaßraum. Mithilfe der zu E assoziierten komplexen Maße Ex,y kann man für gewisse 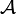 -messbaren Funktion
-messbaren Funktion 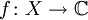 einen (in der Regel unbeschränkten) linearen Operator
einen (in der Regel unbeschränkten) linearen Operatordes Hilbertraumes H erklären. Dieser Operator wird als Spektralintegral von f und der Prozess, durch den er aus f entsteht, als Integration von f bzgl. des Spektralmaßes E bezeichnet.
Spektralmaß eines normalen Operators
Es seien H ein Hilbertraum,
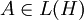 ein normaler Operator mit Spektrum
ein normaler Operator mit Spektrum 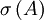 . Dann erklärt man wie folgt ein Spektralmaß
. Dann erklärt man wie folgt ein Spektralmaß 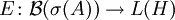 auf der Borelalgebra
auf der Borelalgebra 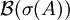 von
von 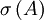 . Es sei
. Es sei 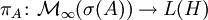 der Funktionalkalkül der beschränkten Borelfunktionen von A. Da πA ein Morphismus von C * -Algebren ist, ist für jede Borelmenge Ω des Spektrums von A durch
der Funktionalkalkül der beschränkten Borelfunktionen von A. Da πA ein Morphismus von C * -Algebren ist, ist für jede Borelmenge Ω des Spektrums von A durch 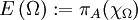 eine orthogonale Projektion von H gegeben. Man kann zeigen, dass
eine orthogonale Projektion von H gegeben. Man kann zeigen, dass 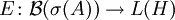 ein Spektralmaß ist, das Spektralmaß des normalen Operators A. Der Spektralsatz für normale Operatoren besagt nun, dass
ein Spektralmaß ist, das Spektralmaß des normalen Operators A. Der Spektralsatz für normale Operatoren besagt nun, dassgilt. Dabei steht auf der rechten Seite dieser Gleichung das Spektralintegral der beschränkten Borelfunktion
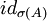 bzgl. des Spektralmaßes E.
bzgl. des Spektralmaßes E.Spektralmaß versus Spektralschar
Definition: Eine Familie
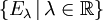 von orthogonalen Projektoren
von orthogonalen Projektoren 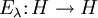 heißt eine Spektralfamilie oder Spektralschar, wenn die folgenden Bedingungen erfüllt sind:
heißt eine Spektralfamilie oder Spektralschar, wenn die folgenden Bedingungen erfüllt sind: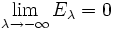 .
.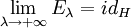 .
.- Die Familie E ist rechtsseitig stetig, in dem Sinne dass
 gilt.
gilt. - Die Familie E ist monoton wachsend: Gilt
 , so gilt
, so gilt 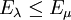 . Diese Bedingung ist äquivalent zu der folgenden Bedingung: Für alle
. Diese Bedingung ist äquivalent zu der folgenden Bedingung: Für alle 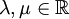 gilt EλEμ = EμEλ = Emin{λ,μ}.
gilt EλEμ = EμEλ = Emin{λ,μ}.
Dabei sind alle auftretenden Limiten im Sinne der starken Operatortopologie, also punktweise zu betrachten.
Der Begriff der Spektralfamilie ging historisch dem Begriff des Spektralmaßes voraus und wurde von John von Neumann unter der Bezeichnung Zerlegung der Einheit eingeführt. Der Zusammenhang zwischen beiden Begriffen ist wie folgt gegeben: Zu jedem reellen Spektralmaß E gehört genau eine Spektralschar
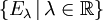 und umgekehrt. Dabei bestimmen sich das Spektralmaß E und die Spektralschar
und umgekehrt. Dabei bestimmen sich das Spektralmaß E und die Spektralschar 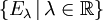 gegenseitig durch die Beziehung
gegenseitig durch die BeziehungDer Träger der Spektralschar
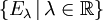 ist die Menge
ist die Menge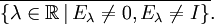 Mithilfe
Mithilfe
einer Spektralschar, deren Träger kompakt ist, kann man in Anlehnung an das Stieltjes-Integrals für eine stetige Funktionen
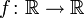 einen, als
einen, alsnotierten, Operator definieren. Dieser ist eindeutig dadurch bestimmt, dass er die Beziehung
erfüllt, wobei nun rechter Hand ein herkömmliches Stieltjes-Integral steht. Es gilt dann
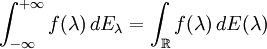 ,
,
wenn E das zu
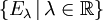 gehörige Spektralmaß bezeichnet.
gehörige Spektralmaß bezeichnet.Spektralmaß eines beschränkten selbstadjungierten Operators
Die Spektralschar eines beschränkten selbstadjungierten Operators hat kompakten Träger in [m,M], wobei
bzw.
sei.
Eλ wird manchmal als Spektralprojektion bezeichnet. Man stellt sich das Bild dieser orthogonalen Projektion als eine Art verallgemeinerter Eigenwertraum vor.
Spektralmaß unbeschränkter selbstadjungierter Operatoren (Quantenmechanik)
Die messbaren Größen der Quantenmechanik entsprechen (fast ausschließlich unbeschränkten) selbstadjungierten Hilbertraum-Operatoren („Observablen“, -> Mathematische Struktur der Quantenmechanik), und zwar mit einer Spektralzerlegung in drei Teile, im Einklang mit den obigen Aussagen:
- Der erste Anteil ist das Punktspektrum (das Spektrum ist abzählbar; die Physiker bezeichnen es irreführenderweise als „diskret“). Hier hat man es mit Summen zu tun.
- Der zweite Anteil ist das absolut-kontinuierliche Spektum (das Spektrum ist kontinuierlich-überabzählbar; die Physiker nennen es einfach „kontinuierlich“). An die Stelle von Summen treten hier gewöhnliche Integrale.
- Sehr selten kommt ein singulär-kontinuierlicher Spektralanteil hinzu (das Spektrum ist eine Cantormenge). Hier muss man mit Stieltjes-Integralen arbeiten (erzeugt durch nicht-differenzierbare monoton-wachsende Funktionen).
Alle Observablen zeigen eine solche Aufteilung und besitzen übliche Spektralmaße und übliche Spektralprojektionen. Die oben genannte Kompaktizität des Spektrums gilt aber nicht.
Die Aufteilung in drei Teile ergibt insgesamt, bei Gewichtung mit den Quadraten aus den Beiträgen der Eigenfunktionen bzw. der verallgemeinerten Eigenfunktionen, genau den Wert 1, im Einklang mit der Wahrscheinlichkeitsinterpretation der Quantenmechanik.
Im (eher seltenen) Fall eines reinen Punktspektrums, der von den Physikern der Einfachheit halber als Normalfall angenommen wird, entsprechen die Spektraleigenschaften dem Postulat von der Vollständigkeit der Eigenfunktionen (Entwicklungssatz). Im Falle eines zusätzlichen absolut-kontinuierlichen Spektralanteils arbeiten die Physiker, wie erwähnt, mit sog. verallgemeinerten Eigenfunktionen und Wellenpaketen (der Zusammenhang mit dem Spektralmaß ergibt sich aus der Distributionstheorie über sog. Gelfandsche Raumtripel). Ein singulär-kontinuierlicher Spektralanteil wird gewöhnlich überhaupt nicht diskutiert, außer z. B. in Kristallen mit speziellen „inkommensurablen“ Magnetfeldern. Näheres in einschlägigen Lehrbüchern der Quantenmechanik und der Maßtheorie reeller Funktionen.
Ursprung
Stichworte
- Hilbert: Spektralformen (Mitteilungen über Integralgleichungen)
- Frigyes Riesz: Les systèmes d'équations linéaires à une infinité d'inconnues. Dort Verallgemeinerung der Hilbertschen Resultate auf selbstadjungierten Operatoren des Hilbertraumes l2.
- von Neumann, Marshall Harvey Stone
- Halmos
- Mackey
Siehe auch
Literatur
- John B. Conway: A Course in Functional Analysis, Springer-Verlag, 1990, 2. Auflage.
- Paul R. Halmos: Introduction to Hilbert space and the theory of spectral multiplicity, Chelsea Publishing Company, 1951, 1. Auflage.
- Harro Heuser: Funktionalanalysis. Theorie und Anwendung., B. G. Teubner-Verlag, Wiesbaden 2006, 4. Auflage, ISBN 3835100262.
- Josef M. Jauch: Foundations of quantum mechanics, Addison-Wesley, 1968, unbekannte Auflage.
- Reinhold Meise und Dietmar Vogt: Einführung in die Funktionalanalysis, Vieweg-Verlag, Wiesbaden, 1992, ISBN 3-528-07262-8.
- John von Neumann: Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren in Math. Ann. (102), 1929, S. 49-131
- Eduard Prugovečki: Quantum Mechanics in Hilbert Space, Dover Publications, 2006, 2. Auflage, ISBN 0486453278.
- Dirk Werner: Funktionalanalysis, Springer-Verlag, 2005, 5. Auflage.
- U. Krey, A.Owen: Basic Theoretical Physics - A Concise Overview, especially part III. Springer, 2007, ISBN 978-3-540-36804-5
- Es gilt
Wikimedia Foundation.


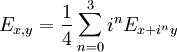
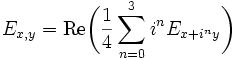
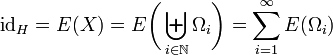

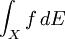
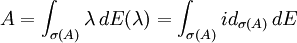
![E_{\lambda}=E((-\infty,\lambda])\quad,\quad\lambda\in\mathbb{R}.](/pictures/dewiki/50/2ee5ba9b1873b2b1449f49dbac83d255.png)