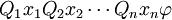- Quantifizierte boolesche Formel
-
In der Komplexitätstheorie ist das Erfüllbarkeitsproblem für quantifizierte boolesche Formeln (oft nur kurz QBF oder QSAT) eine Verallgemeinerung des Erfüllbarkeitsproblems der Aussagenlogik. Es untersucht, ob eine mit Quantoren versehene aussagenlogische Formel erfüllbar oder wahr ist. Es ist das kanonische PSPACE-vollständige Problem.
Inhaltsverzeichnis
Quantifizierte boolesche Formeln
Jede aussagenlogische Formel kann durch Hinzufügen von All- und Existenzquantoren erweitert werden. Die Semantik einer so gebildeten Formel ähnelt der Semantik prädikatenlogischer Formeln.
Syntax
Die Menge der quantifizierten boolescher Formeln kann wie folgt induktiv definiert werden:
- Jede Aussagenvariable x ist eine quantifizierte boolesche Formel. x tritt in der Formel x frei auf
- Sind
 und ψ quantifizierte boolesche Formeln, so auch
und ψ quantifizierte boolesche Formeln, so auch 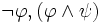 und
und 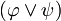 . Eine Aussagenvariable x aus
. Eine Aussagenvariable x aus  oder ψ ist frei in den Formeln, falls x in
oder ψ ist frei in den Formeln, falls x in  oder ψ frei ist.
oder ψ frei ist. - Ist
 eine quantifizierte boolesche Formel und x eine Aussagenvariable, so sind auch
eine quantifizierte boolesche Formel und x eine Aussagenvariable, so sind auch 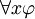 und
und 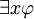 quantifizierte boolesche Formeln. Der Gültigkeitsbereich von
quantifizierte boolesche Formeln. Der Gültigkeitsbereich von 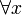 beziehungsweise
beziehungsweise 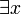 erstreckt sich auf jedes freies Vorkommen von x in
erstreckt sich auf jedes freies Vorkommen von x in  . Jede andere nicht gebundene Aussagenvariable ist frei in
. Jede andere nicht gebundene Aussagenvariable ist frei in 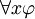 und
und 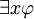 .
.
Semantik
Die Semantik quantifizierter boolescher Formeln orientiert sich eng an die Semantik der Prädikatenlogik: Der Wert einer quantifizierten booleschen Formel der Form
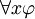 wird bestimmt, indem
wird bestimmt, indem  durch
durch 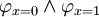 ersetzt wird, wobei
ersetzt wird, wobei 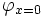 und
und 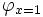 dadurch entstehen, dass jedes Auftreten von x durch 0 beziehungsweise 1 ersetzt wird. Analog dazu wird jedes Aufkommen von
dadurch entstehen, dass jedes Auftreten von x durch 0 beziehungsweise 1 ersetzt wird. Analog dazu wird jedes Aufkommen von 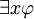 durch
durch 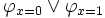 ersetzt.
ersetzt.Eine Formel, die keine freie Variablen enthält, ist damit entweder wahr oder falsch.
Pränexe Normalform
Eine quantifizierte boolesche Formel ist in pränexer Normalform, falls sie von der Form
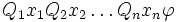 ist, wobei
ist, wobei 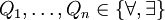 und
und 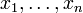 Variablen einer aussagenlogischen Formel
Variablen einer aussagenlogischen Formel  ohne Quantoren sind. Der Ausdruck
ohne Quantoren sind. Der Ausdruck 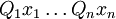 heißt Quantorenblock.
heißt Quantorenblock.Da für jede quantifizierte boolesche Formel eine äquivalente Formel in pränexer Normalform existiert und diese in Polynomialzeit konstruiert werden kann, wird häufig in Beweisen von dieser Form ausgegangen.
Das Erfüllbarkeitsproblem
Das Erfüllbarkeitsproblem für quantifizierte boolesche Formeln ist es, zu entscheiden, ob eine gegebene quantifizierte boolesche Formel ohne freie Variablen wahr oder falsch ist.
Aus der Definition der Semantik für quantifizierte boolesche Formeln lässt sich ein einfacher rekursiver Algorithmus ableiten, der das Erfüllbarkeitsproblem für quantifizierte boolesche Formeln in pränexer Normalform löst: Bei Eingabe einer Formel der Form
für eine aussagenlogische Formel
 und Quantoren
und Quantoren 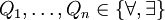 wird der Wert von
wird der Wert von  berechnet, falls keine Quantoren vorhanden sind. Andernfalls wird im Fall
berechnet, falls keine Quantoren vorhanden sind. Andernfalls wird im Fall 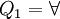 der Wert von
der Wert von 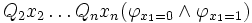 und im Fall
und im Fall 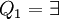 der Wert von
der Wert von 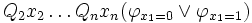 berechnet.
berechnet.Bei einer quantifizierten booleschen Formel mit n Quantoren benötigt der Algorithmus also O(2n) Schritte. Allerdings ist der benötigte Speicherplatz quadratisch in der Länge der Formel, das Problem liegt also in PSPACE. Weiterhin konnte gezeigt werden, dass das Entscheidungsproblem PSPACE-schwer ist.[1] Dieses Problem ist damit vollständig für die Klasse PSPACE.
Quantorenwechsel und Polynomialzeithierarchie
Aus der Struktur des Quantorenblocks einer quantifizierten booleschen Formel in Präfix-Normalform lassen sich Rückschlüsse auf komplexitätstheoretische Eigenschaften ziehen. Die Klassen der wahren quantifizierten booleschen Formeln in Präfix-Normalform sind je nach Anzahl der Alternationen von All- und Existenzquantoren und deren Reihenfolge vollständig für eine Stufe der Polynomialzeithierarchie. Im folgenden ist für einen Quantor
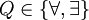 QXi die Schreibweise für Qxi1,Qxi2,...,Qxik für eine beliebige Zahl k.
QXi die Schreibweise für Qxi1,Qxi2,...,Qxik für eine beliebige Zahl k.Ist Σk die Klasse aller wahren quantifizierten booleschen Formeln ohne freie Variablen der Form
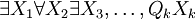 mit
mit 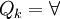 , falls k gerade ist und andernfalls
, falls k gerade ist und andernfalls 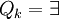
und Πk die Klasse aller wahren quantifizierten booleschen Formeln ohne freie Variablen der Form
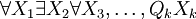 mit
mit 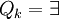 , falls k gerade ist und andernfalls
, falls k gerade ist und andernfalls 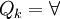 ,
,
so gilt für alle
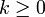 :
:- Σk ist
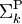 -vollständig und
-vollständig und - Πk ist
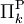 -vollständig.[2]
-vollständig.[2]
Einzelnachweise und Quellen
Wikimedia Foundation.