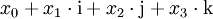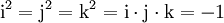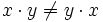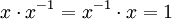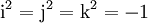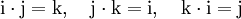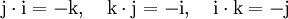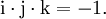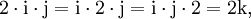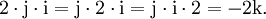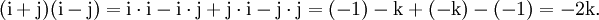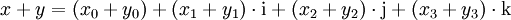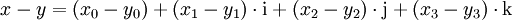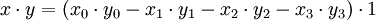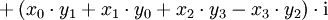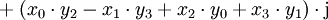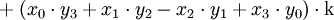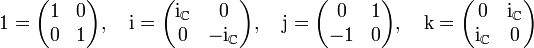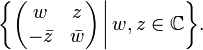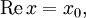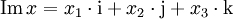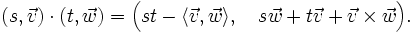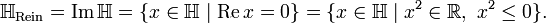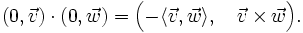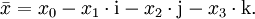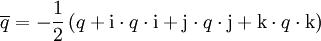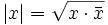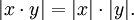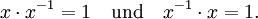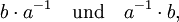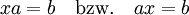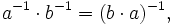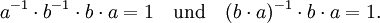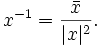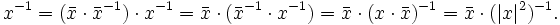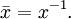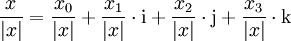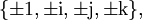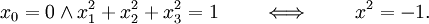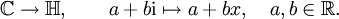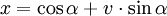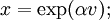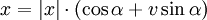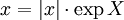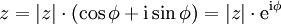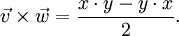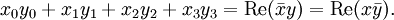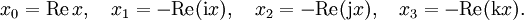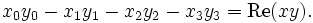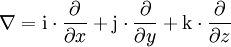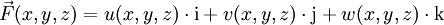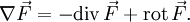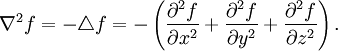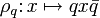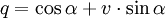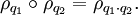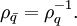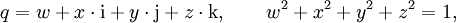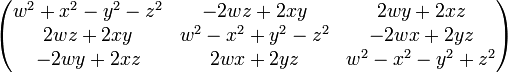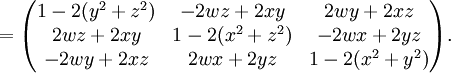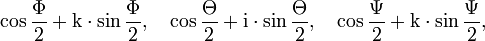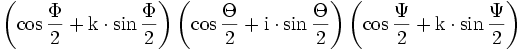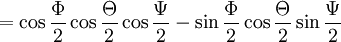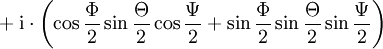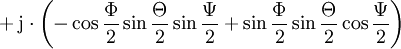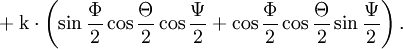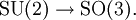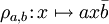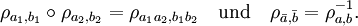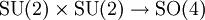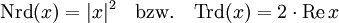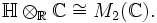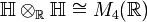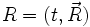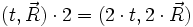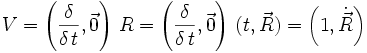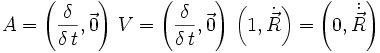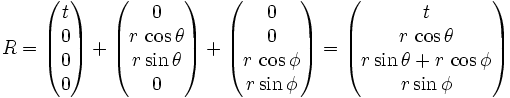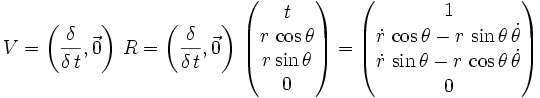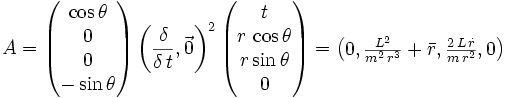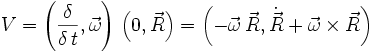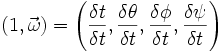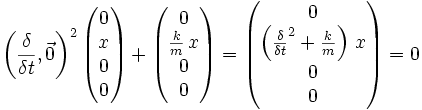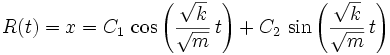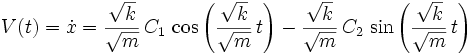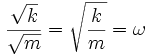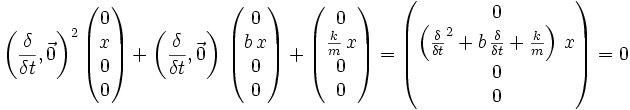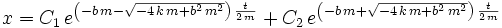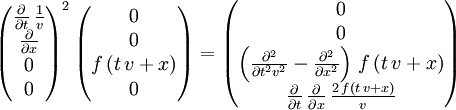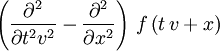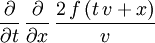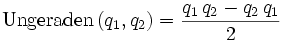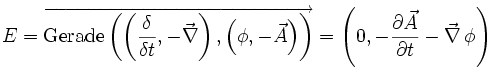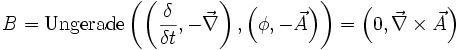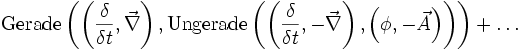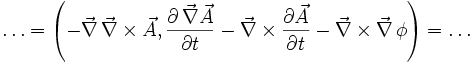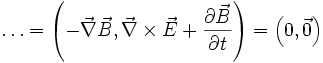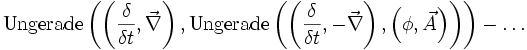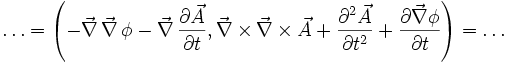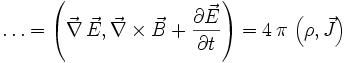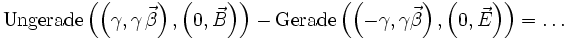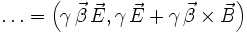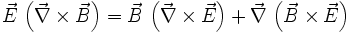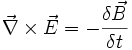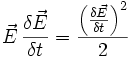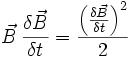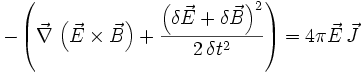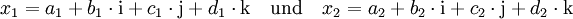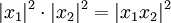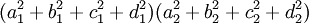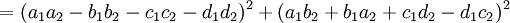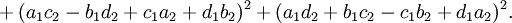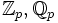- Quaternionen
-
 Gedenktafel an der Broom Bridge in Dublin, wo William Rowan Hamilton die Multiplikationsregeln im Oktober 1843 spontan in den Stein ritzte.
Gedenktafel an der Broom Bridge in Dublin, wo William Rowan Hamilton die Multiplikationsregeln im Oktober 1843 spontan in den Stein ritzte.Die Quaternionen (von lat. quaternio „Vierheit“) sind eine Erweiterung der reellen Zahlen, ähnlich den komplexen Zahlen. Erdacht wurden sie 1843 von Sir William Rowan Hamilton; sie werden deshalb auch hamiltonsche Quaternionen oder Hamilton-Zahlen genannt. Unabhängig von Hamilton entdeckte sie 1840 Olinde Rodrigues. Die Menge der Quaternionen wird meistens mit
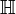 bezeichnet. (Man beachte jedoch, dass dieses Symbol je nach Kontext auch eine andere Bedeutung haben kann, siehe obere Halbebene und hyperbolischer Raum.)
bezeichnet. (Man beachte jedoch, dass dieses Symbol je nach Kontext auch eine andere Bedeutung haben kann, siehe obere Halbebene und hyperbolischer Raum.)Quaternionen erlauben in vielen Fällen eine rechnerisch elegante Beschreibung des dreidimensionalen Raumes, insbesondere im Kontext von Drehungen. Sie sind aber auch als eigenständiges mathematisches Objekt von Interesse.
Die Quaternionen entstehen aus den reellen Zahlen durch Hinzufügung dreier neuer Zahlen i, j und k, jede Quaternion lässt sich eindeutig in der Form
mit reellen Zahlen x0, x1, x2, x3 schreiben. Die neuen Zahlen i, j, k werden gemäß den Hamilton-Regeln
multipliziert. Die Multiplikation ist nicht kommutativ, d. h. für zwei Quaternionen x und y sind die beiden Produkte
im Allgemeinen verschieden. Einige aus dem Reellen bekannte Rechenregeln gelten deshalb für Quaternionen nicht, Assoziativgesetz und Distributivgesetz bleiben jedoch erhalten.
Die Quaternionen bilden einen Schiefkörper; das bedeutet insbesondere, dass es zu jeder Quaternion
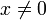 eine inverse Quaternion x − 1 gibt, so dass
eine inverse Quaternion x − 1 gibt, so dassgilt. (Die Notation
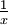 wird aufgrund der Nichtkommutativität vermieden, siehe unten.) Die Quaternionen sind eine vierdimensionale
wird aufgrund der Nichtkommutativität vermieden, siehe unten.) Die Quaternionen sind eine vierdimensionale  -Algebra.
-Algebra.Rechenregeln
Die Konstruktion der Quaternionen ist der der komplexen Zahlen analog, allerdings wird nicht eine Zahl, deren Quadrat −1 ergibt, hinzugefügt, sondern drei, nämlich i, j und k.
Beim Rechnen mit Quaternionen der Form
mit reellen Zahlen x0,x1,x2,x3 kann man i,j,k wie anti-kommutierende Variable behandeln; treten Produkte von zweien von ihnen auf, so darf man sie nach den Hamilton-Regeln
ersetzen. Unter Voraussetzung der ersten Regel sind die anderen beiden äquivalent zu
Reelle Faktoren kommutieren mit i,j,k, d. h. es gilt beispielsweise
aber
Nicht alle aus der elementaren Algebra bekannten Rechenregeln gelten für die Quaternionen, z. B. gilt
Die binomische Formel (a + b)(a − b) = a2 − b2 ist hier aber nicht anwendbar, sie setzt voraus, dass ab = ba gilt.
Für zwei Quaternionen
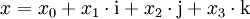 und
und 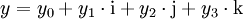
ist also
Zur Division siehe unten.
Konstruktionen
Zur Konstruktion der Quaternionen gibt es mehrere Möglichkeiten, deren wesentliche Schritte im folgenden skizziert werden.
Vierervektoren
Oben wurden die Quaternionen lediglich durch ihre Eigenschaften beschrieben. Eine mögliche Definition besteht darin, die Quaternionen mit Vektoren im Raum
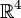 zu identifizieren und die Multiplikation entsprechend den obigen Regeln zu übertragen. Dass es sich um eine
zu identifizieren und die Multiplikation entsprechend den obigen Regeln zu übertragen. Dass es sich um eine  -Algebra handelt, muss dann noch im Detail nachgewiesen werden.
-Algebra handelt, muss dann noch im Detail nachgewiesen werden.Komplexe Matrizen
Eine andere Konstruktion fasst die Quaternionen als Unterring des Rings
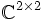 der komplexen
der komplexen 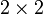 -Matrizen auf. Dabei setzt man
-Matrizen auf. Dabei setzt man(Zur Verdeutlichung wurde die imaginäre Einheit der komplexen Zahlen als
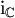 notiert.)
notiert.)Es gibt verschiedene Möglichkeiten für diese Realisierung, die alle zueinander konjugiert sind; in der oben angegebenen sind die Matrizen für i,j,k gerade
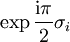 mit den Pauli-Matrizen σi aus der Quantenmechanik, siehe auch unten.
mit den Pauli-Matrizen σi aus der Quantenmechanik, siehe auch unten.Die Menge aller Quaternionen entspricht dabei
Insbesondere ist die Determinante gleich | w | 2 + | z | 2, daraus folgt die Nullteilerfreiheit und damit die Existenz von multiplikativen Inversen für
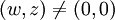 .
.Bei der Konstruktion als Matrizen sind auch die weiteren Eigenschaften wie Assoziativgesetz klar, es muss also lediglich noch die Gültigkeit der hamiltonschen Multiplikationsregeln für i,j,k nachgewiesen werden.
Quotientenalgebra
Die theoretisch einfachste, aber auch abstrakteste Konstruktion ist der Quotient des nichtkommutativen Polynomrings in drei Unbestimmten, deren Bilder i,j,k sind, nach dem Ideal, das von den Hamilton-Regeln erzeugt wird. Es genügt auch, stattdessen nur zwei Unbestimmte zu verwenden.
Grundlegende Operationen
Skalarteil und Vektorteil
Aufgrund der besonderen Stellung der Komponente x0 einer Quaternion
bezeichnet man sie (wie bei den komplexen Zahlen) als Realteil oder Skalarteil
während die Komponenten x1,x2,x3 zusammen den Imaginärteil oder Vektorteil
bilden. Häufig identifiziert man den Vektorteil auch mit dem Vektor (x1,x2,x3) in
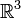 .
.Identifiziert man in dieser Weise Quaternionen
mit Paaren aus einem Skalar und einem Vektor in
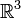
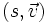 mit s = x0 und
mit s = x0 und 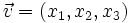 ,
,
so lässt sich die Multiplikation mithilfe von Skalarprodukt und Vektorprodukt beschreiben:
Quaternionen, deren Vektorteil 0 ist, werden mit den ihrem Skalarteil entsprechenden reellen Zahlen identifiziert.
Eine Quaternion, deren Realteil 0 ist, nennt man reine Quaternion (auch: rein imaginär oder vektoriell). Reine Quaternionen lassen sich auch als diejenigen Quaternionen charakterisieren, deren Quadrat reell und nichtpositiv ist. Für die Menge der reinen Quaternionen schreibt man
Sie ist ein dreidimensionaler reeller Vektorraum mit Basis {i,j,k}.
Für reine Quaternionen nimmt die Multiplikation eine besonders einfache Form an:
Konjugation und Betrag
Zu jeder Quaternion
ist die konjugierte Quaternion definiert als
Die Konjugation lässt also den Skalarteil unverändert und ist die Multiplikation mit −1 auf dem Vektorteil. Alternativ lässt sich die Konjugation auch als
darstellen.
Die wichtigsten Eigenschaften der Konjugation sind:
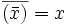 (die Konjugation ist eine Involution);
(die Konjugation ist eine Involution);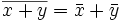 und
und
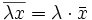 für reelle Zahlen λ, d. h. die Konjugation ist
für reelle Zahlen λ, d. h. die Konjugation ist  -linear;
-linear;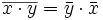
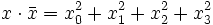 , insbesondere ist dieser Wert reell und nichtnegativ.
, insbesondere ist dieser Wert reell und nichtnegativ.
Aus der letzten Eigenschaft ergibt sich auch, dass der Wert
gerade der gewöhnliche Betrag des Vektors (x0,x1,x2,x3) ist; man nennt ihn auch den Betrag oder die Länge der Quaternion x. Er erfüllt die wichtige Eigenschaft
Mit dem Betrag werden die Quaternionen zu einer reellen Banachalgebra.
Wie bei komplexen Zahlen kann man auch Skalar- und Vektorteil mithilfe der Konjugation beschreiben:
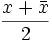 ist der Skalarteil;
ist der Skalarteil;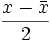 ist der Vektorteil.
ist der Vektorteil.
Ist eine Quaternion gleich ihrer Konjugierten, so ist sie reell, d. h. der Vektorteil ist null. Ist eine Quaternion gleich dem Negativen ihrer Konjugierten, so ist sie eine reine Quaternion, d. h. der Skalarteil ist null.
Inverse und Division
Die Konjugation erlaubt es, genau wie bei komplexen Zahlen, inverse Quaternionen anzugeben. Das multiplikative Inverse zu jeder Quaternion
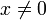 erfüllt definitionsgemäß die Gleichungen
erfüllt definitionsgemäß die GleichungenMit Hilfe des multiplikativen Inversen lassen sich zwei Arten der Division definieren, nämlich
die die jeweiligen Lösungen der Gleichungen
sind. Sie stimmen im allgemeinen nur dann überein, wenn der Nenner a reell ist; deshalb kann die Schreibweise
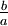 dort verwendet werden, bei allgemeinen Quaternionen wäre dies jedoch nicht eindeutig.
dort verwendet werden, bei allgemeinen Quaternionen wäre dies jedoch nicht eindeutig.Außerdem gilt die Formel
da
Damit kann man das multiplikative Inverse einer Quaternion
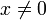 berechnen als
berechnen alsDenn
Da | x | 2 reell und
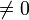 (wegen
(wegen 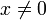 ) ist, kann es als Bruch
) ist, kann es als Bruch 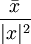 geschrieben werden.
geschrieben werden.Einheitsquaternionen
Eine Einheitsquaternion (auch: normierte Quaternion, Quaternion der Länge 1) ist eine Quaternion, deren Betrag gleich 1 ist. Für sie gilt (analog zu den komplexen Zahlen)
Für eine beliebige Quaternion
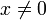 ist
isteine Einheitsquaternion, die man manchmal auch als das Signum von x bezeichnet.
Das Produkt zweier Einheitsquaternionen und das Inverse einer Einheitsquaternion sind wieder Einheitsquaternionen; die Einheitsquaternionen bilden also eine Gruppe.
Zu den Einheitsquaternionen zählen insbesondere die acht Quaternionen
die eine Untergruppe der Einheitsquaternionen bilden, die Quaternionengruppe.
Geometrisch kann man die Menge der Einheitsquaternionen als die Einheits-3-Sphäre im vierdimensionalen euklidischen Raum und damit als Lie-Gruppe interpretieren. Die zugehörige Lie-Algebra ist der Raum der reinen Quaternionen. In der Matrixdarstellung entsprechen die Einheitsquaternionen genau der Gruppe SU(2), dies erklärt auch den Bezug zu den Pauli-Matrizen.
Einheitsquaternionen, die auch reine Quaternionen sind, lassen sich als diejenigen Quaternionen charakterisieren, deren Quadrat −1 ergibt:
Geometrisch entsprechen sie der 2-Sphäre im dreidimensionalen Raum. Jede Quaternion mit Quadrat − 1 definiert eine Einbettung der komplexen Zahlen in die Quaternionen
Dies ist allerdings nur eine Einbettung von
 -Algebren, die Quaternionen sind keine Algebra über
-Algebren, die Quaternionen sind keine Algebra über  .
.Polardarstellung
Jede Einheitsquaternion
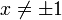 kann auf eindeutige Weise in der Form
kann auf eindeutige Weise in der Formmit
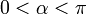 und einer reinen Einheitsquaternion
und einer reinen Einheitsquaternion 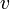 dargestellt werden. Mit der verallgemeinerten Exponentialfunktion lässt sich dies wegen
dargestellt werden. Mit der verallgemeinerten Exponentialfunktion lässt sich dies wegen 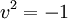 auch schreiben als
auch schreiben alsanders gesagt: die Exponentialabbildung ist eine Bijektion von der Menge der reinen Quaternionen vom Betrag
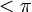 auf die Menge der Einheitsquaternionen mit Ausnahme von − 1.
auf die Menge der Einheitsquaternionen mit Ausnahme von − 1.Allgemeiner lässt sich jede nicht reelle Quaternion eindeutig in der Form
mit α,v wie oben schreiben oder jede nicht reell-negative Quaternion eindeutig als
mit einer reinen Quaternion X mit
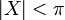 .
.Diese Darstellungen sind der Polarform komplexer Zahlen
vollkommen analog.
Beschreibung anderer Konstruktionen mit Hilfe von Quaternionen
Produkte
- Das Kreuzprodukt der Vektorteile zweier Quaternionen ist bis auf den Faktor 2 ihr Kommutator: Ist
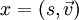 und
und 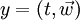 , so gilt
, so gilt
- Das Skalarprodukt zweier Quaternionen, aufgefasst als Vektoren im
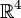 , ist der Skalarteil von
, ist der Skalarteil von 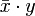 oder von
oder von 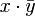 :
:
-
- Insbesondere kann man damit die einzelnen Komponenten einer Quaternion isolieren:
- Das Minkowski-Skalarprodukt zweier Quaternionen, aufgefasst als Vektoren im Minkowski-Raum, ist der Skalarteil von xy:
Vektoranalysis
Im folgenden werden reine Quaternionen mit Vektoren im dreidimensionalen Raum
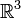 identifiziert. Definiert man den Nabla-Operator (wie Hamilton) als
identifiziert. Definiert man den Nabla-Operator (wie Hamilton) alsund wendet ihn auf ein Vektorfeld
an, so erhält man
(Dabei ist
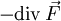 der Skalarteil,
der Skalarteil, 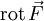 der Vektorteil der Quaternion.)
der Vektorteil der Quaternion.)Zweimalige Anwendung von
 auf eine Funktion f(x,y,z) ergibt
auf eine Funktion f(x,y,z) ergibtDrehungen im dreidimensionalen Raum
Einheitsquaternionen können für eine elegante Beschreibung von Drehungen im dreidimensionalen Raum verwendet werden: Für eine feste Einheitsquaternion q ist die Abbildung
auf
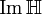 eine Drehung. (Hier wie im folgenden ist nur von Drehungen die Rede, die den Ursprung festlassen, d. h. deren Drehachse durch den Ursprung verläuft.)
eine Drehung. (Hier wie im folgenden ist nur von Drehungen die Rede, die den Ursprung festlassen, d. h. deren Drehachse durch den Ursprung verläuft.)Schreibt man die Einheitsquaternion q wie oben als
mit
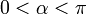 und einer reinen Einheitsquaternion
und einer reinen Einheitsquaternion 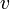 , so handelt es sich um die Drehung mit Drehwinkel
, so handelt es sich um die Drehung mit Drehwinkel 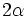 um die Achse, die der Einheitsvektor
um die Achse, die der Einheitsvektor 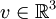 aufspannt.
aufspannt.Für jede Einheitsquaternion q definieren q und − q dieselbe Drehung; insbesondere entsprechen 1 und − 1 beide der identischen Abbildung (Drehung mit Drehwinkel 0). Im Unterschied zur Beschreibung von Drehungen durch orthogonale Matrizen handelt es sich also um keine 1:1-Entsprechung, zu jeder Drehung R gibt es genau zwei Einheitsquaternionen q mit ρq = R.
Die Hintereinanderausführung von Drehungen entspricht der Multiplikation der Quaternionen, d. h.
Die Umkehrung der Drehrichtung entspricht der Konjugation:
Bezug zu orthogonalen Matrizen
Die einer Einheitsquaternion
entsprechende orthogonale Matrix ist
Für die umgekehrte Umwandlung von Drehmatrizen in Quaternionen genügt es, Drehwinkel und -achse zu bestimmen und in die weiter oben angegebene Formel einzusetzen.
Bezug zu Eulerwinkeln
Für Eulerwinkel gibt es verschiedene Konventionen; die folgenden Ausführungen beziehen sich auf die Drehung, die man erhält, wenn man zuerst um die z-Achse um den Winkel Φ, dann um die neue x-Achse um den Winkel Θ und schließlich um die neue z-Achse um den Winkel Ψ dreht. Die Einzeldrehungen entsprechen den Quaternionen
und da jeweils um die mitgedrehten Achsen gedreht wird, ist die Reihenfolge der Komposition umgekehrt, die Gesamtdrehung entspricht also
Für andere Konventionen ergeben sich ähnliche Formeln.
Die Eulerwinkel zu einer gegebenen Quaternion lassen sich an der zugehörigen Drehmatrix ablesen.
Universelle Überlagerung der Drehgruppe
Die Konstruktion
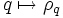 liefert einen Homomorphismus der Gruppe der Einheitsquaternionen in die Drehgruppe, mithilfe der Identifizierung der Einheitsquaternionen mit der Gruppe SU(2) also auch
liefert einen Homomorphismus der Gruppe der Einheitsquaternionen in die Drehgruppe, mithilfe der Identifizierung der Einheitsquaternionen mit der Gruppe SU(2) also auchEs handelt sich um eine zweiblättrige Überlagerung, der Kern ist das Zentrum
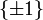 . Da
. Da 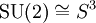 einfach zusammenhängend ist, handelt es sich um die universelle Überlagerung. Sie wird auch Spingruppe Spin(3) genannt, die natürliche Operation von SU(2) auf
einfach zusammenhängend ist, handelt es sich um die universelle Überlagerung. Sie wird auch Spingruppe Spin(3) genannt, die natürliche Operation von SU(2) auf 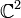 ist eine Spinordarstellung.
ist eine Spinordarstellung.Orthogonale Abbildungen des vierdimensionalen Raumes
Analog zum dreidimensionalen Fall kann man jede orientierungserhaltende orthogonale Abbildung von
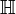 in sich selbst in der Form
in sich selbst in der Formfür Einheitsquaternionen a,b beschreiben. Es gilt
Diese Konstruktion liefert eine Überlagerung
mit Kern {(1,1),( − 1, − 1)}.
Die Quaternionen als Algebra
Es gibt bis auf Isomorphie genau drei endlichdimensionale
 -Algebren, die Schiefkörper sind, nämlich
-Algebren, die Schiefkörper sind, nämlich  selbst, die komplexen Zahlen
selbst, die komplexen Zahlen  und die Quaternionen
und die Quaternionen 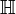 .
.Das Zentrum von
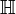 ist
ist  ; die Quaternionen sind also eine zentraleinfache Algebra über
; die Quaternionen sind also eine zentraleinfache Algebra über  . Reduzierte Norm und Spur sind durch
. Reduzierte Norm und Spur sind durchgegeben.
Beim Basiswechsel von
 zum algebraischen Abschluss
zum algebraischen Abschluss  werden die Quaternionen zu einer Matrizenalgebra:
werden die Quaternionen zu einer Matrizenalgebra:Die komplexe Konjugation auf dem Faktor
 des Tensorproduktes entspricht einer Involution der Matrizenalgebra, deren Invarianten eine zu
des Tensorproduktes entspricht einer Involution der Matrizenalgebra, deren Invarianten eine zu 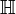 isomorphe Algebra bilden. Die Involution
isomorphe Algebra bilden. Die Involution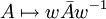 mit
mit 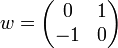
entspricht dem oben angegebenen Matrizenmodell der Quaternionen.
Die Tatsache, dass die Brauergruppe von
 nur aus zwei Elementen besteht, spiegelt sich auch darin wider, dass
nur aus zwei Elementen besteht, spiegelt sich auch darin wider, dassist.
Allgemein bezeichnet man jede vierdimensionale zentraleinfache Algebra über einem Körper als eine Quaternionenalgebra.
Die Quaternionen sind die Clifford-Algebra zum Raum
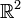 mit einer negativ definiten symmetrischen Bilinearform.
mit einer negativ definiten symmetrischen Bilinearform.Anwendungen
Die Darstellung von Drehungen mithilfe von Quaternionen wird heutzutage im Bereich der interaktiven Computergrafik genutzt, insbesondere bei Computerspielen, sowie bei der Steuerung und Regelung von Satelliten. Bei Verwendung von Quaternionen an Stelle von Drehmatrizen werden etwas weniger Rechenoperationen benötigt. Insbesondere, wenn viele Drehungen miteinander kombiniert (multipliziert) werden, steigt die Verarbeitungsgeschwindigkeit. Des Weiteren werden Quaternionen, neben den Eulerwinkeln, zur Programmierung von Industrierobotern (z. B. ABB) genutzt.
Physik
Durch die Verwendung der Quaternionen kann man in vielen Fällen auf getrennte Gleichungen zur Berechnung von Zeit und Raum verzichten. Dies bietet Vorteile in der Physik, unter anderem in den Gebieten Mechanik, Wellengleichungen, Spezielle Relativitätstheorie und Gravitation, Elektromagnetismus sowie der Quantenmechanik.
Beschreibung einer Bewegung
Die Position eines „Punktes“ zu einem bestimmten Zeitpunkt kann beispielsweise als
beschrieben werden, wobei der Vektor
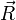 die räumliche Position des Punktes in Relation zum Ursprung und t den Zeitpunkt angibt. Hieraus ist auch die Bewegung des Punktes ersichtlich, da sich z. B. nach der doppelten Zeit der Punkt doppelt so weit bewegt haben wird:
die räumliche Position des Punktes in Relation zum Ursprung und t den Zeitpunkt angibt. Hieraus ist auch die Bewegung des Punktes ersichtlich, da sich z. B. nach der doppelten Zeit der Punkt doppelt so weit bewegt haben wird:Durch Differentiation über die Zeit erhält man daraus die Geschwindigkeit, bzw. durch nochmalige Differentiation die Beschleunigung, inklusive Angabe der Richtung:
Hier zeigt sich der Vorteil der Verwendung von Quaternionen, da keine getrennten Gleichungen zur Berechnung der gesuchten Größe und zur Berechnung der Richtung, in die die Größe wirkt, nötig sind.
Beschreibung einer Drehung
Natürlich kann man dies auch in Polarkoordinaten darstellen. Für eine z. B. zweidimensionale Fläche ergibt sich der Punkt R aus
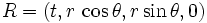 .
.
Für den dreidimensionalen Raum muss man hierfür die im Abschnitt Polardarstellung gezeigte Beschreibungsweise verwenden bzw. eine weitere Quaternion mit dem jeweiligen anderen Winkel definieren und die beiden Quaternionen addieren. Die Herleitung sieht also wie folgt aus:
wobei θ den Winkel in der XY-Ebene und φ den Winkel in der YZ-Ebene darstellt (siehe: Eulerwinkel).
Natürlich kann man auch die Polardarstellung differenzieren, wodurch sich für die radiale Geschwindigkeit V und radiale Beschleunigung A im zweidimensionalen Raum der folgende Zusammenhang ergibt:
-
A 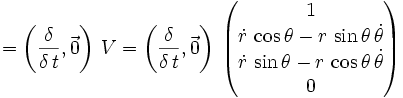
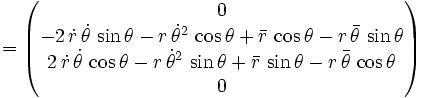
Für die Drehung im dreidimensionalen Raum kann man auch hier die Geschwindigkeiten und Beschleunigungen zur Vereinfachung getrennt berechnen und anschließend addieren.
Zur Berechnung der Zentripetalbeschleunigung setzt man die Zentralkraft mit
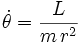 sowie
sowie 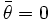 ein und lässt die Quaternion um ihre Achse drehen.
ein und lässt die Quaternion um ihre Achse drehen.wobei
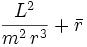 die Beschleunigung in radialer Richtung (zum Mittelpunkt) und
die Beschleunigung in radialer Richtung (zum Mittelpunkt) und 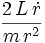 die Beschleunigung in tangentialer Richtung darstellt. Obwohl diese Beschreibung komplizierter zu verstehen ist, hat diese Rechnungsweise auch hier den Vorteil, dass getrennte Gleichungen nicht notwendig sind.
die Beschleunigung in tangentialer Richtung darstellt. Obwohl diese Beschreibung komplizierter zu verstehen ist, hat diese Rechnungsweise auch hier den Vorteil, dass getrennte Gleichungen nicht notwendig sind.Beschreibung einer Rotation
Die Rotation ist im Wesentlichen eine fortlaufende Drehung. Diese wird durch die Rotationsgeschwindigkeit (bzw. Winkelgeschwindigkeit) ω ausgedrückt. Die Geschwindigkeit des Punktes R um die Drehachse ist somit definiert durch:
Hierbei gilt es zu beachten, dass die Zeit t in der Position R nicht erscheint, da diese in ω enthalten ist, das vorab differenziert wurde:
Die Beschleunigung der Rotation ist wieder analog definiert durch die Differentiation der Geschwindigkeit:
-
A 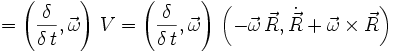
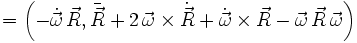
Hierbei beschreibt
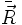 eine Translation (geradlinige Bewegung),
eine Translation (geradlinige Bewegung), 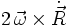 beschreibt die Coriolisbewegung und
beschreibt die Coriolisbewegung und 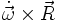 beschreibt die Bewegung in Richtung des Azimut (daher aus der Rotationsebene heraus). Der Term
beschreibt die Bewegung in Richtung des Azimut (daher aus der Rotationsebene heraus). Der Term 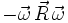 kann in
kann in 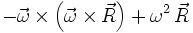 umgeformt werden, der die Zentrifugalkraft beschreibt. Dieses zeigt sich vor allem für den Fall, dass die Rotation orthogonal (d. h. im Rechten Winkel zur Drehachse) ist, wobei gilt:
umgeformt werden, der die Zentrifugalkraft beschreibt. Dieses zeigt sich vor allem für den Fall, dass die Rotation orthogonal (d. h. im Rechten Winkel zur Drehachse) ist, wobei gilt: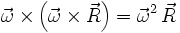 sowie
sowie 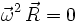
Die Bedeutung des skalaren Ausdrucks
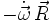 ist bisher nicht endgültig geklärt.
ist bisher nicht endgültig geklärt.Harmonischer Oszillator
Ein harmonischer Oszillator in einer Dimension (X-Achse) kann in quaternionischer Schreibweise als
ausgedrückt werden. Aus dieser Gleichung lässt sich x lösen, woraus sich die Gleichung
ergibt. Um etwa die Geschwindigkeit zum Zeitpunkt t zu erhalten muss man diese Gleichung mit der Zeit differenzieren. Dadurch ergibt sich der Zusammenhang:
Hierbei ist:
und damit die Winkelgeschwindigkeit.
Gedämpfter Harmonischer Oszillator
Der gedämpfte harmonische Oszillator lässt sich analog zum ungedämpften harmonischen Oszillator ableiten. Für eine Dimension ergibt sich somit:
und nach Auflösen zu x:
Wellengleichung
Eine Welle, die sich in Richtung der X-Achse ausbreitet kann durch die Gleichung
beschrieben werden. Hierbei ist
die Amplitude und damit die allgemeine Wellengleichung, während
dem durch die Welle übertragenen Impuls p entspricht.
Siehe auch: Klein-Gordon-Gleichung
Elektromagnetismus
Die Maxwellgleichungen zur Beschreibung des Elektromagnetismus sind der bekannteste Anwendungsfall für Quaternionen. Die Maxwellgleichungen werden durch eine Gruppe von Kommutatoren und Antikommutatoren des Differenzoperators, des elektrischen Feldes E und dem magnetischen Feld B im Vakuum definiert. Im Wesentlichen sind dieses die homogene Maxwellgleichung und das Gaußsche Gesetz.
Im Folgenden werden modifizierte Kommutatoren und Antikommutatoren verwendet:
Die homogene Maxwellgleichung ist definiert durch:
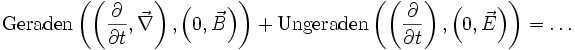
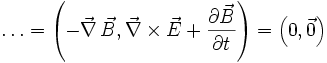 .
.
Hierbei besagt
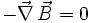 , dass keine magnetischen Monopole existieren.
, dass keine magnetischen Monopole existieren. 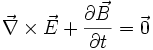 ist das Faradaysche Induktionsgesetz.
ist das Faradaysche Induktionsgesetz.Das Gaußsche Gesetz definiert sich umgekehrt aus:
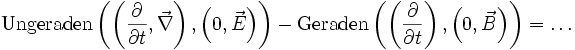
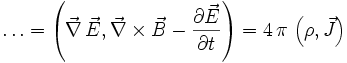 .
.
Hierbei ist
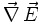 das Gaußsche Gesetz und
das Gaußsche Gesetz und 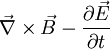 das von Maxwell korrigierte Ampèresche Durchflutungsgesetz.
das von Maxwell korrigierte Ampèresche Durchflutungsgesetz.Elektromagnetisches Vierpotenzial
Die elektrischen und magnetischen Felder werden häufig als elektromagnetisches Viererpotential (d. h. als 4-wertiger Vektor) ausgedrückt. Dieser Vektor kann auch als Quaternion umformuliert werden.
Das elektrische Feld E ist der Antikommutator des konjungierten, differenzierten Vierpotenzials. Das magnetische Feld B verwendet den Kommutator. Durch diese Darstellungsform kann man direkt in die Maxwellgleichungen einsetzen:
sowie
Hierbei sind die Ausdrücke
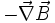 und
und 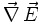 die beiden Quellenfelder, die durch die Differenz aus zwei Kommutatoren und zwei Antikommutatoren gebildet werden.
die beiden Quellenfelder, die durch die Differenz aus zwei Kommutatoren und zwei Antikommutatoren gebildet werden.Das Induktionsgesetz
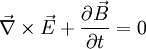 und das Durchflutungsgesetz
und das Durchflutungsgesetz 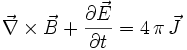 werden durch die Summe aus den zwei ineinanderliegenden Kommutatoren und Antikommutatoren gebildet.
werden durch die Summe aus den zwei ineinanderliegenden Kommutatoren und Antikommutatoren gebildet.Lorentzkraft
Die Lorentzkraft wird auf ähnliche Weise aus den Maxwellgleichungen abgeleitet. Allerdings müssen die Vorzeichen korrigiert werden.
Erhaltungssatz
Der Erhaltungssatz der elektrischen Ladung wird durch die Anwendung des konjugierten Differenzoperators auf die Quellen der Maxwellgleichung gebildet.
-
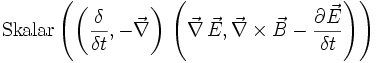
= 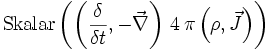
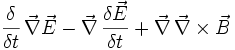
= 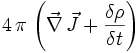
Diese Gleichung zeigt, dass das Skalarprodukt des elektrischen Feldes E plus dem Kreuzprodukt des magnetischen Feldes B auf der einen Seite, sowie der Stromdichte J plus der Frequenz der Ladungsdichte ρ auf der anderen Seite, gleich ist. Dieses bedeutet, dass die Ladung bei der Umformung erhalten bleibt.
Poyntings Energieerhaltungssatz wird in auf dieselbe Weise abgeleitet, mit dem Unterschied, dass statt dem Differenzial das konjungierte elektrische Feld
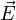 verwendet wird.
verwendet wird.-
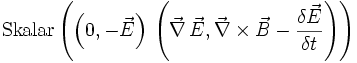
= 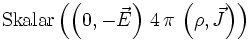
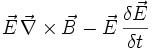
= 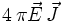
Mit Hilfe der Vektoridentitäten
kann man diese Gleichung nach
umformen, was der Poynting-Gleichung entspricht. Der Ausdruck
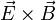 entspricht hierbei dem Poynting-Vektor.
entspricht hierbei dem Poynting-Vektor.Vier-Quadrate-Satz
Sind
zwei Quaternionen, so ergibt sich aus der Gleichung
die rein reelle Identität
Sind alle beteiligten Zahlen ai,bi,ci,di ganz, so besagt diese Gleichung, dass das Produkt zweier Zahlen, die sich als Summe von vier Quadratzahlen schreiben lassen, selbst eine Summe von vier Quadratzahlen ist.
Der Vier-Quadrate-Satz besagt, dass jede natürliche Zahl Summe von vier Quadratzahlen ist, und die eben genannte Aussage erlaubt es, sich beim Beweis auf Primzahlen zu beschränken: Sind Primzahlen als Summen von vier Quadraten darstellbar, so auch Produkte von Primzahlen, aber jede natürliche Zahl ist Produkt von Primzahlen, damit ergibt sich die Behauptung. Aufgrund dieses Zusammenhanges wird auch die obige Identität manchmal als Vier-Quadrate-Satz bezeichnet.
Geschichte
William Rowan Hamilton hatte 1835 die Konstruktion der komplexen Zahlen als Zahlenpaare angegeben. Dadurch motiviert, suchte er lange nach einer entsprechenden Struktur auf dem Raum
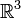 der Zahlentripel; heute weiß man, dass es keine derartige Struktur mit guten Eigenschaften gibt. 1843 schließlich gelangte er zu der Erkenntnis, dass es möglich ist, eine Multiplikation auf der Menge der 4-Tupel zu konstruieren, wenn man dazu bereit ist, die Kommutativität aufzugeben. In einem Brief an seinen Sohn gibt er als Datum den 16. Oktober 1843 an und berichtet, er habe sich spontan dazu hinreißen lassen, die Multiplikationsregeln in einen Stein an der Brougham Bridge (heute Broombridge Road) in Dublin zu ritzen; später wurde dort eine Gedenktafel angebracht. Die Rechenregeln für Quaternionen waren in Ansätzen schon früher bekannt, so findet sich die Formel für den Vier-Quadrate-Satz bereits bei Leonhard Euler (1748). Andere, auch allgemeinere Multiplikationsregeln wurden von Hermann Graßmann untersucht (1855).
der Zahlentripel; heute weiß man, dass es keine derartige Struktur mit guten Eigenschaften gibt. 1843 schließlich gelangte er zu der Erkenntnis, dass es möglich ist, eine Multiplikation auf der Menge der 4-Tupel zu konstruieren, wenn man dazu bereit ist, die Kommutativität aufzugeben. In einem Brief an seinen Sohn gibt er als Datum den 16. Oktober 1843 an und berichtet, er habe sich spontan dazu hinreißen lassen, die Multiplikationsregeln in einen Stein an der Brougham Bridge (heute Broombridge Road) in Dublin zu ritzen; später wurde dort eine Gedenktafel angebracht. Die Rechenregeln für Quaternionen waren in Ansätzen schon früher bekannt, so findet sich die Formel für den Vier-Quadrate-Satz bereits bei Leonhard Euler (1748). Andere, auch allgemeinere Multiplikationsregeln wurden von Hermann Graßmann untersucht (1855).Schon kurz nach der Entdeckung der Quaternionen fand Hamilton die Darstellung von Drehungen des Raumes mithilfe von Quaternionen und damit eine erste Bestätigung der Bedeutung der neuen Struktur; Arthur Cayley entdeckte 1855 die entsprechenden Aussagen über orthogonale Abbildungen des vierdimensionalen Raumes. Die bloße Parametrisierung der
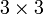 -Drehmatrizen war hingegen schon Euler bekannt. Cayley gab 1858 in der Arbeit, in der er Matrizen einführte, auch die Möglichkeit der Darstellung von Quaternionen durch komplexe
-Drehmatrizen war hingegen schon Euler bekannt. Cayley gab 1858 in der Arbeit, in der er Matrizen einführte, auch die Möglichkeit der Darstellung von Quaternionen durch komplexe 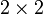 -Matrizen an.
-Matrizen an.Hamilton widmete sich fortan ausschließlich dem Studium der Quaternionen; sie wurden in Dublin ein eigenes Examensfach. In seiner Nachfolge wurde 1895 sogar ein „Weltbund zur Förderung der Quaternionen“ gegründet. Der deutsche Mathematiker Felix Klein schreibt rückblickend über diese anfängliche Euphorie:
„Wie ich schon andeutete, schloß sich Hamilton eine Schule an, die ihren Meister an Starrheit und Intoleranz noch überbot. […] Die Quaternionen sind gut und brauchbar an ihrem Platze; sie reichen aber in ihrer Bedeutung an die gewöhnlichen komplexen Zahlen nicht heran. […] Die Leichtigkeit und Eleganz, mit der sich hier die weittragendsten Theoreme ergeben, ist in der Tat überraschend, und es läßt sich wohl von hier aus die alles andere ablehnende Begeisterung der Quaternionisten für ihr System begreifen, die […] nun bald über vernünftige Grenzen hinauswuchs, in einer weder der Mathematik als Ganzem noch der Quaternionentheorie selbst förderlichen Weise. […] Die Verfolgung des angegebenen Weges – der neu sein will, obwohl er tatsächlich nur eine peinlich genaue Übertragung längst bekannter Gedanken auf ein einziges neues Objekt, also durchaus keine geniale Konzeption bedeutet – führt zu allerhand Erweiterungen der bekannten Sätze, die in ihrer Allgemeinheit das Hauptcharakteristikum verlieren und gegenstandslos werden, allenfalls zu Besonderheiten, die ein gewisses Vergnügen gewähren mögen.“
– Felix Klein: Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert[1]
Verwandte Themen
Ähnliche Konstruktionen wie die Quaternionen werden manchmal unter dem Namen „hyperkomplexe Zahlen“ zusammengefasst. Beispielsweise sind die Cayley-Zahlen oder Oktaven ein achtdimensionales Analogon zu den Quaternionen; ihre Multiplikation ist allerdings weder kommutativ noch assoziativ.
Literatur
- Arthur S. Hathaway: A Primer of Quaternions. Gutenberg eText
- Max Koecher, Reinhold Remmert: Hamiltonsche Quaternionen. In: H.-D. Ebbinghaus et al.: Zahlen. Springer-Verlag, Berlin 1983. ISBN 3-540-12666-X
- John H. Conway, Derek A. Smith: On Quaternios and Octonions, A K Peters Ltd, 2003, ISBN 1-56881-134-9 (englisch)
- Jack B. Kuipers: Quaternions and Rotation Sequences, Princeton University Press, 2002, ISBN 0-691-10298-8 (englisch)
- W. Bolton: Complex Numbers (Mathematics for Engineers), Addison Wesley, 1996, ISBN 0-582-23741-6 (englisch)
- Andrew J. Hanson: Visualizing Quaternions, Morgan Kaufmann Publishers, 2006, ISBN 0-12-088400-3 (englisch)
Quellen
- Doing Physics with Quaternions (PDF)
- Serge Lang, Algebra. Springer-Verlag, New York 2002. ISBN 0-387-95385-X
Weblinks
- Hamilton's Quaternions – eine englische Einführung (Post Script)
- Quaternionen in der Computeranimation
- Kurze Einführung (PDF)
- Quaternionische Fraktale (PDF) Abschlussarbeit über quaternionische Fraktale
- Der Ort der Entdeckung der Quaternionen (mit Bildern)
Einzelnachweise
- ↑ Felix Klein: Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert. Teil I., Verlag von Julius Springer, Berlin 1926, S. 184ff.
Natürliche Zahlen
 | Ganze Zahlen
| Ganze Zahlen  | Rationale Zahlen
| Rationale Zahlen  | Reelle Zahlen
| Reelle Zahlen  | Komplexe Zahlen
| Komplexe Zahlen  | Quaternionen
| Quaternionen 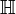 | Oktaven
| Oktaven 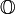
Wikimedia Foundation.