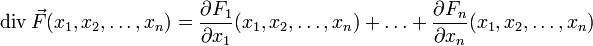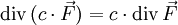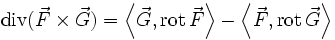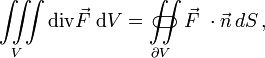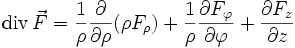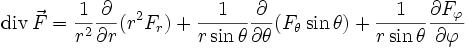- Quellenfrei
-
Unter der Divergenz versteht man in der Mathematik ein bestimmtes Funktional eines Vektorfeldes. Interpretiert man dieses Feld als Strömungsfeld, so gibt die Divergenz für jede Stelle die Tendenz an, ob ein Teilchen in der Nähe zu diesem Punkt hin- bzw. von diesem Punkt wegfließt. Es sagt damit aus, ob und wo das Vektorfeld Quellen (Divergenz größer als Null) oder Senken (Divergenz kleiner als Null) hat. Ist die Divergenz überall gleich Null, so bezeichnet man das Feld als quellenfrei.
Inhaltsverzeichnis
Beispiel aus der Physik
Man betrachtet zum Beispiel eine ruhige Wasseroberfläche, auf die ein dünner Strahl Öl trifft. Die Bewegung des Öls auf der Oberfläche kann durch ein zweidimensionales (zeitabhängiges) Vektorfeld beschrieben werden, d. h. zu jedem Zeitpunkt ist die Fließgeschwindigkeit (und -richtung) des Ölfilms in jedem Punkt angegeben. Die Stelle, an der der Strahl auf die Wasseroberfläche trifft, ist eine „Ölquelle“, da von dort Öl wegfließt, ohne Zufluss auf der Oberfläche. Die Divergenz in der Nähe dieser Stelle ist positiv. Im Gegensatz dazu bezeichnet man die Stelle, an der das Öl beispielsweise am Rand aus dem Wasserbecken abfließt, als Senke. Die Divergenz in der Nähe dieser Stelle ist negativ.
Verbal lässt sich die Divergenz eines Vektorfeldes v(x,y,z) wie folgt formulieren. Sie ist die Summe über alle Komponenten von der schrittweitebezogenen Vergrößerung der jeweiligen Komponente, wenn man einen infinitesimalen Schritt in positive Komponentenrichtung geht.
Die Divergenz lässt sich formal als Ableitungsoperator interpretieren und gehört zusammen mit den anderen Ableitungsoperatoren Gradient und Rotation der Vektoranalysis an, einem Untergebiet der mehrdimensionalen Analysis.
Formale Definition
Die Divergenz eines Vektorfeldes
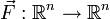 ist ein skalares Feld. Es wird als
ist ein skalares Feld. Es wird als 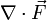 oder als
oder als 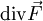 geschrieben. Dabei bezeichnet
geschrieben. Dabei bezeichnet  den formalen Nabla-Operator und
den formalen Nabla-Operator und 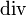 das Operatorsymbol der Divergenz. Für den Fall eines dreidimensionalen Vektorfeldes
das Operatorsymbol der Divergenz. Für den Fall eines dreidimensionalen Vektorfeldes  ist die Divergenz in kartesischen Koordinaten definiert als
ist die Divergenz in kartesischen Koordinaten definiert alsAllgemein gilt für ein n-dimensionales Vektorfeld
 das jedem Punkt eines n-dimensionalen Raumes einen n-Vektor zuordnet:
das jedem Punkt eines n-dimensionalen Raumes einen n-Vektor zuordnet:Die Divergenz lässt sich formal als Skalarprodukt zwischen
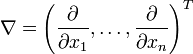 und
und 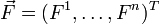 interpretieren, d. h. als die Summe der komponentenweisen Produkte.
interpretieren, d. h. als die Summe der komponentenweisen Produkte.Die Divergenz als „Quellendichte“
Man kann das Vektorfeld
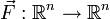 als Strömungsfeld interpretieren, mit einer (skalaren) Quellen- und einer (vektoriellen) Wirbeldichte (n=3) Die Divergenz kann in diesem Sinne als „Quellendichte“ (im Gegensatz zur „Wirbeldichte“, siehe Rotation (Mathematik)) interpretiert werden
als Strömungsfeld interpretieren, mit einer (skalaren) Quellen- und einer (vektoriellen) Wirbeldichte (n=3) Die Divergenz kann in diesem Sinne als „Quellendichte“ (im Gegensatz zur „Wirbeldichte“, siehe Rotation (Mathematik)) interpretiert werdenFür die Interpretation der Divergenz als „Quellendichte“ ist die folgende koordinatenfreie Definition wichtig (hier für den Fall n=3)
Dabei ist ΔV ein beliebiges Volumen, z. B. eine Kugel oder ein Parallelepiped; | ΔV | ist sein Inhalt. Es wird über den Rand
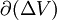 dieses Volumenelements integriert;
dieses Volumenelements integriert; 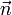 ist die nach außen gerichtete Normale und dS das zugehörige Flächenelement.
ist die nach außen gerichtete Normale und dS das zugehörige Flächenelement.Für n > 3 kann diese Aussage leicht verallgemeinert werden, indem man n-dimensionale Volumina und ihre (n-1)-dimensionalen Randflächen betrachtet. Bei Spezialisierung auf infinitesimale Würfel oder Quader erhält man die bekannte Darstellung in kartesischen Koordinaten
In orthogonalen krummlinigen Koordinaten, z. B. Kugelkoordinaten, elliptischen Koordinaten, usw., (also für
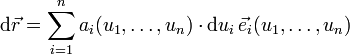 , mit
, mit 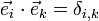 (=1 für i=k, =0 sonst), wobei
(=1 für i=k, =0 sonst), wobei  ist, wobei also nicht die dui, sondern die
ist, wobei also nicht die dui, sondern die 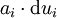 die physikalische Dimension einer „Länge“ haben, gilt dagegen etwas allgemeiner
die physikalische Dimension einer „Länge“ haben, gilt dagegen etwas allgemeiner![\operatorname{div}\, \vec{F} = (a_1 \cdot a_2 \cdot \ldots \cdot a_n)^{-1}\,\left\{ \frac{\partial}{\partial u_1}[(a_2 \cdot a_3\cdot \ldots \cdot a_{n-1} \cdot a_n)\,F_1] + \dots \right\},](/pictures/dewiki/49/101a6551dbd5a706901bf367e961e6fa.png) wobei die Punkte am Ende weitere Terme beinhalten, die durch fortgesetzte zyklische Permutationen, erzeugt nach dem Schema
wobei die Punkte am Ende weitere Terme beinhalten, die durch fortgesetzte zyklische Permutationen, erzeugt nach dem Schema 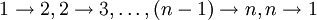 , usw., aus dem angeschriebenen folgen.
, usw., aus dem angeschriebenen folgen.
Herleitung der kartesischen Darstellung
Zur Herleitung der kartesischen Darstellung der Divergenz aus der koordinatenfreien Darstellung betrachte einen infinitesimalen Würfel
![[x_{1},x_{1}+\Delta x_{1}],\ldots,[x_{n},x_{n}+\Delta x_{n}]](/pictures/dewiki/102/fcd9a9649006825edaabe3f0b0b298ae.png) .
.Nun wendet man den Mittelwertsatz der Integralrechnung an, wobei die gestrichenen Größen x'i aus dem Intervall [xi,xi + Δxi] sind.
Somit bleibt nur die Summe der Differenzenquotienten übrig
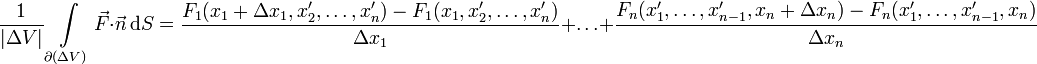 ,
,
die im Grenzübergang
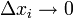 zu partiellen Ableitungen werden:
zu partiellen Ableitungen werden:Ein „Zerlegungs-Theorem“
Für n=3-dimensionale Vektorfelder
 , die im ganzen Raum mindestens zweimal stetig differenzierbar sind und im Unendlichen hinreichend rasch gegen Null gehen, gilt, dass sie in einen wirbelfreien Teil
, die im ganzen Raum mindestens zweimal stetig differenzierbar sind und im Unendlichen hinreichend rasch gegen Null gehen, gilt, dass sie in einen wirbelfreien Teil 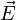 und einen quellenfreien Teil
und einen quellenfreien Teil  zerfallen,
zerfallen, 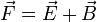 . Für den wirbelfreien Teil gilt, dass er durch seine Quellendichte wie folgt dargestellt werden kann:
. Für den wirbelfreien Teil gilt, dass er durch seine Quellendichte wie folgt dargestellt werden kann: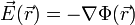 , mit
, mit
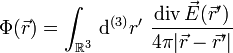 .
.Für den quellenfreien Teil,
 , gilt analoges, wenn man das skalare Potential Φ durch ein sog. Vektorpotential
, gilt analoges, wenn man das skalare Potential Φ durch ein sog. Vektorpotential 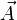 ersetzt und zugleich die Ausdrücke
ersetzt und zugleich die Ausdrücke  bzw.
bzw. 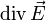 (=Quellendichte von
(=Quellendichte von 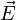 ) durch die Operationen
) durch die Operationen 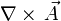 bzw.
bzw. 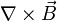 (=Wirbeldichte von
(=Wirbeldichte von  ) substituiert.
) substituiert.Rechenregeln
Sei c eine Konstante, u ein skalares Feld und
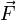 ,
, 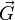 jeweils ein Vektorfeld. Dann gelten folgende Regeln:
jeweils ein Vektorfeld. Dann gelten folgende Regeln:Produktregeln
Die Produktregeln ergeben sich aus den Produktregeln von Differentialformen.
Dabei sind bei der ersten Regel u eine 0-Form und F eine 2-Form, wobei bei der zweiten Regel F und G 1-Formen sind.
Integralsatz
Eine wichtige Rolle spielt die Divergenz beim Gaußschen Integralsatz. Er besagt, dass der Durchfluss durch eine geschlossene Oberfläche gleich dem Integral über die Divergenz des Vektorfeldes im Inneren dieses Volumens ist und erlaubt damit die Umwandlung eines Volumenintegrals in ein Oberflächenintegral:
wobei
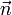 der Normalenvektor der Oberfläche
der Normalenvektor der Oberfläche 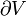 ist. Anschaulich beschreibt er damit für den Fall einer Strömung den Zusammenhang zwischen dem Durchfluss durch diese Fläche und den Strömungsquellen und Senken innerhalb des zugehörigen Volumens.
ist. Anschaulich beschreibt er damit für den Fall einer Strömung den Zusammenhang zwischen dem Durchfluss durch diese Fläche und den Strömungsquellen und Senken innerhalb des zugehörigen Volumens.Zylinder- und Kugelkoordinaten
In Zylinderkoordinaten gilt für die Divergenz eines Vektorfeldes
 :
:In Kugelkoordinaten gilt für die Divergenz eines Vektorfeldes
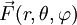 :
:Inverse
Unter gewissen Voraussetzungen existiert eine Rechts- oder Linksinverse der Divergenz. So gibt es für ein lipschitz-stetiges Gebiet
 einen Operator
einen Operator  , so dass für jedes
, so dass für jedes  mit
mit 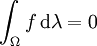
gilt, wobei Wm,p(Ω) den entsprechenden Sobolew-Raum für
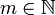 und
und 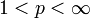 bezeichnet. B heißt Bogowksii-Operator.[1]
bezeichnet. B heißt Bogowksii-Operator.[1]Literatur
- Adolf J. Schwab: Begriffswelt der Feldtheorie, Springer Verlag, ISBN 3-540-42018-5
Quellen
- ↑ G. P. Galdi, An introduction to the mathematical theory of the Navier-Stokes equations. Vol. I, Springer Tracts in Natural Philosophy, vol. 38, Springer-Verlag, New York, 1994, ISBN 0-387-94172-X
Weblinks
Wikimedia Foundation.

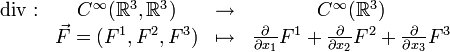
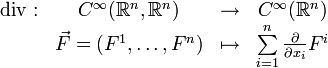
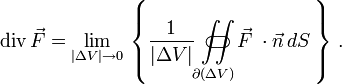
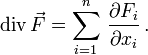
![\begin{align}
\frac{1}{|\Delta V|}\int\limits _{\partial(\Delta V)}\vec{F}\cdot\vec{n}\,\mathrm{d}S & =\frac{1}{\Delta x_{1}\Delta x_{2}\ldots\Delta x_{n}}\left[\int\limits _{x_{2}}^{x_{2}+\Delta x_{2}}\ldots\int\limits _{x_{n}}^{x_{n}+\Delta x_{n}}\left(\vec{F}(x_{1}+\Delta x_{1},x_{2},\ldots,x_{n})-\vec{F}(x_{1},x_{2},\ldots,x_{n})\right)\cdot\hat{e}_{1}\,\mathrm{d}x_{2}\ldots\mathrm{d}x_{n}\right]+\ldots\\
& +\frac{1}{\Delta x_{1}\Delta x_{2}\ldots\Delta x_{n}}\left[\int\limits _{x_{1}}^{x_{1}+\Delta x_{1}}\ldots\int\limits _{x_{n-1}}^{x_{n-1}+\Delta x_{n-1}}\left(\vec{F}(x_{1},\ldots,x_{n-1},x_{n}+\Delta x_{n})-\vec{F}(x_{1},\ldots,x_{n-1},x_{n})\right)\cdot\hat{e}_{n}\,\mathrm{d}x_{1}\ldots\mathrm{d}x_{n-1}\right]\end{align}](/pictures/dewiki/51/3b5fbac9974b9653eca1f296dbfed2a6.png)
![\begin{align}
\frac{1}{|\Delta V|}\int\limits _{\partial(\Delta V)}\vec{F}\cdot\vec{n}\,\mathrm{d}S & =\frac{\left(\vec{F}(x_{1}+\Delta x_{1},x'_{2},\ldots,x'_{n})-\vec{F}(x_{1},x'_{2},\ldots,x'_{n})\right)\cdot\hat{e}_{1}}{\Delta x_{1}}\underbrace{\left[\frac{1}{\Delta x_{2}}\int\limits _{x_{2}}^{x_{2}+\Delta x_{2}}\mathrm{d}x_{2}\right.}_{=1}\ldots\underbrace{\left.\frac{1}{\Delta x_{n}}\int\limits _{x_{n}}^{x_{n}+\Delta x_{n}}\mathrm{d}x_{n}\right]}_{=1}+\ldots\\
& +\frac{\left(\vec{F}(x'_{1},\ldots,x'_{n-1},x_{n}+\Delta x_{n})-\vec{F}(x'_{1},\ldots,x'_{n-1},x_{n})\right)\cdot\hat{e}_{n}}{\Delta x_{n}}\left[\frac{1}{\Delta x_{1}}\int\limits _{x_{1}}^{x_{1}+\Delta x_{1}}\mathrm{d}x_{1}\ldots\frac{1}{\Delta x_{n-1}}\int\limits _{x_{n-1}}^{x_{n-1}+\Delta x_{n-1}}\mathrm{d}x_{n-1}\right]\end{align}](/pictures/dewiki/52/4ffc608c33c87ee65614afe225b1bb19.png)