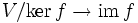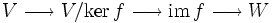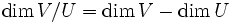- Quotientenvektorraum
-
Der Faktorraum ist ein Begriff aus der linearen Algebra, einem Teilgebiet der Mathematik. Er ist derjenige Vektorraum, der als Bild einer Parallelprojektion entlang eines Unterraumes entsteht.
Inhaltsverzeichnis
Definition
Es sei V ein Vektorraum über einem Körper K und U ein Unterraum von V. Wir definieren eine Äquivalenzrelation auf V durch
d.h. wenn sich v1 und v2 um einen Vektor aus U unterscheiden, oder anders gesagt: wenn die Gerade durch die Punkte v1 und v2 parallel zu U ist.
Die Äquivalenzklasse eines Punktes v ist
anschaulich der zu U "parallele" affine Unterraum durch v. Die Äquivalenzklassen werden auch als Nebenklassen bezeichnet; dieser Begriff stammt aus der Gruppentheorie.
Die Menge der Äquivalenzklassen wird mit V / U bezeichnet und heißt der Faktorraum von V nach U. Er bildet einen Vektorraum, wenn man die Vektorraumoperationen vertreterweise definiert:
- [v1] + [v2] = [v1 + v2]
![\lambda\cdot[v] = [\lambda v]](/pictures/dewiki/57/9f9d116b8c685105838d3d9738c4949c.png)
für
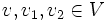 und
und 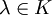 .
.Eigenschaften
- Es gibt eine kanonische surjektive lineare Abbildung
- Ist W ein Komplement von U in V, d.h. ist V die direkte Summe von U und W, so ist die Einschränkung von π auf W ein Isomorphismus. Es gibt aber keine kanonische Möglichkeit, V / U als Unterraum von V aufzufassen.
- Der Dualraum von V / U kann mit denjenigen Linearformen auf V identifiziert werden, die auf U identisch 0 sind.
- Der Homomorphiesatz besagt, dass eine lineare Abbildung
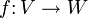 einen Isomorphismus
einen Isomorphismus
-
- zwischen dem Faktorraum von V nach dem Kern von f und dem Bild von f induziert, d.h. die Verkettung
- ist gleich f.
- Die Dimension eines Faktorraums lässt sich folgendermaßen berechnen (falls V endlich-dimensional ist):
-
- Dies folgt durch Anwenden der Dimensionsformel für lineare Abbildungen auf die kanonische Abbildung, da U gerade ihr Kern ist.
Anwendung in der Funktionalanalysis
Viele normierte Räume entstehen auf die folgende Weise: Sei V ein reeller oder komplexer Vektorraum und sei p eine Halbnorm auf V. Dann ist
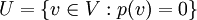 ein Untervektorraum von V. Der Faktorraum V / U wird dann mit der Norm
ein Untervektorraum von V. Der Faktorraum V / U wird dann mit der Norm ![[v] \mapsto p(v)](/pictures/dewiki/102/f8e4a0fc9d3d53b578fc360f75de8851.png) ein normierter Vektorraum.
ein normierter Vektorraum.Allgemeiner: Sei V ein topologischer Vektorraum, der nicht hausdorffsch ist. Dann lässt sich analog zu oben ein Unterraum definieren:
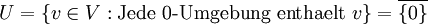 . Der Faktorraum V / U wird dann mit der Quotiententopologie ein Hausdorffscher topologischer Vektorraum.
. Der Faktorraum V / U wird dann mit der Quotiententopologie ein Hausdorffscher topologischer Vektorraum.Beispiele
- Die Lp-Räume und damit auch die Sobolew-Räume sind Faktorräume
Siehe auch
Wikimedia Foundation.

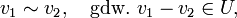
![[v]=v+U = \{v+u\mid u\in U\},](/pictures/dewiki/54/62ac593d79adfec802edebde0840424e.png)
![\pi\colon V\to V/U,\quad v\mapsto[v].](/pictures/dewiki/48/0b26a8726655edb5b819e986832bcada.png)