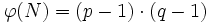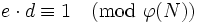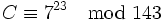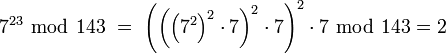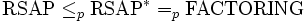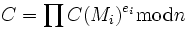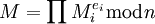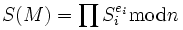RSA-Kryptologiesystem

RSA ist ein asymmetrisches Kryptosystem, das sowohl zur Verschlüsselung als auch zur digitalen Signatur verwendet werden kann. Es verwendet ein Schlüsselpaar bestehend aus einem privaten Schlüssel, der zum Entschlüsseln oder Signieren von Daten verwendet wird, und einem öffentlichen Schlüssel, mit dem man verschlüsselt oder Signaturen prüft. Der private Schlüssel wird geheim gehalten und kann nicht oder nur mit extrem hohem Aufwand aus dem öffentlichen Schlüssel berechnet werden.

Geschichte

RSA wurde 1977 von Ronald L. Rivest, Adi Shamir und Leonard Adleman am MIT entwickelt. Der Name RSA steht für die Anfangsbuchstaben dieser Namen. Es galt damals als das erste asymmetrische Verschlüsselungsverfahren.

Bereits Anfang der 1970er Jahre war im Government Communications Headquarters von Ellis, Cocks und Williamson ein ähnliches asymmetrisches Verfahren entwickelt worden, welches aber keine große praktische Bedeutung erlangte und aus Geheimhaltungsgründen nicht wissenschaftlich publiziert wurde [1].

RSA konnte daher 1983 zum Patent angemeldet werden, obgleich es nicht das erste Verfahren dieser Art war. Das Patent ist am 21. September 2000 ausgelaufen.

Hybride Verfahren

RSA ist im Vergleich zu 3DES und AES mindestens um einen Faktor 1.000 langsamer. Für die Verschlüsselung größerer Datenmengen werden daher symmetrische Verfahren eingesetzt. Es genügt jedoch, RSA zum Austausch eines Schlüssels für die symmetrische Verschlüsselung zu benutzen.

Verfahren

Nachdem Whitfield Diffie und Martin Hellman eine Theorie zur Public-Key-Kryptografie veröffentlicht hatten, versuchten die drei Mathematiker Rivest, Shamir und Adleman, die Annahmen von Diffie und Hellman zu widerlegen. Nachdem sie den Beweis bei verschiedenen Verfahren durchführen konnten, stießen sie schließlich auf eines, bei dem sie keinerlei Angriffspunkte fanden. Hieraus entstand dann RSA.

Das Verfahren wurde 1977 entwickelt und basiert auf dem aktuellen Wissensstand, dass die Faktorisierung einer großen Zahl, also ihre Zerlegung in ihre Primfaktoren, eine sehr aufwändige Angelegenheit ist, während das Erzeugen einer Zahl durch Multiplikation zweier Primzahlen recht einfach ist. Wenn nun eine Nachricht einem Empfänger verschlüsselt zugeleitet werden soll, generiert dieser einen öffentlichen Schlüssel. Der Nachrichtenabsender verwendet diesen öffentlich bekanntgemachten Schlüssel, indem er damit seine Botschaft verschlüsselt. Nur der Empfänger kann diese entschlüsseln, da nur er die „Zusammensetzung“ des von ihm erzeugten (öffentlichen) Schlüssels kennt.

Einwegfunktionen

Funktionen wie die Multiplikation/Faktorisierung, bei denen eine Richtung leicht, die andere schwierig zu berechnen ist, bezeichnet man als Einwegfunktionen (engl. one-way function). Um allerdings die Entschlüsselung tatsächlich möglich zu machen, muss es sich um Falltürfunktionen (engl. trap door one-way function) handeln, die mit Hilfe einer Zusatzinformation auch rückwärts leicht zu berechnen sind.

Das Verfahren ist mit dem Rabin-Verschlüsselungsverfahren verwandt.

Erzeugung des öffentlichen und privaten Schlüssels

Der öffentliche Schlüssel (public key) ist ein Zahlenpaar (e,N) und der private Schlüssel (private key) ein Zahlenpaar (d,N), wobei N bei beiden Schlüsseln gleich ist. Man nennt N den RSA-Modul, e den Verschlüsselungsexponenten und d den Entschlüsselungsexponenten. Diese Zahlen werden durch das folgende Verfahren erzeugt:

1. Wähle zufällig und stochastisch unabhängig zwei Primzahlen 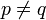$p \neq q$. In der Praxis rät man dazu jeweils eine Zahl und führt mit dieser anschließend einen Primzahltest durch.
2. Berechne den RSA-Modul

   $N = p \cdot q$.

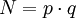3. Berechne die Eulersche φ-Funktion von N

   $\varphi(N) = (p-1) \cdot (q-1)$

4. Wähle eine zu 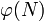$\varphi(N)$ teilerfremde Zahl e, für die gilt $1 < e < \varphi(N)$.
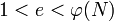5. Berechne den Entschlüsselungsexponenten d als Multiplikativ Inverses von e bezüglich des Modulus 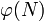$\varphi(N)$. Es soll also die folgende Kongruenz gelten

   $e \cdot d \equiv 1 \pmod{\varphi(N)}$

Die Zahlen p, q und 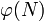$\varphi(N)$ werden nicht mehr benötigt und sollten nach der Schlüsselerstellung auf sichere Weise gelöscht werden. Aus Effizienzgründen wird e klein gewählt, üblich ist 2¹⁶ + 1 = 65537. Kleinere Werte von e können zu Angriffsmöglichkeiten führen, etwa in Form des von Johan Hastad publizierten „Broadcast“-Angriffs, bei dem der Versand einer Nachricht an mehrere Empfänger zu einer Dechiffrierung über den chinesischen Restsatz führen kann.^[1] Bei Wahl eines d mit weniger als einem Viertel der Bits des RSA-Moduls kann d – sofern nicht bestimmte Zusatzbedingungen erfüllt sind – mit einem auf Kettenbrüchen aufbauenden Verfahren effizient ermittelt werden.^[2]

Beispiel

1. Wir wählen p = 11 und q = 13 für die beiden Primzahlen.
2. Der RSA-Modul ist $N = p \cdot q = 143$.
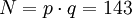3. Die eulersche φ-Funktion nimmt damit den Wert 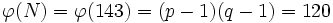$\varphi(N) = \varphi(143) = (p-1)(q-1) = 120$ an.
4. Die Zahl e muss zu 120 teilerfremd sein. Wir wählen e = 23. Damit bilden e = 23 und N = 143 den öffentlichen Schlüssel.
5. Berechnung der Inversen zu e:
   Es gilt: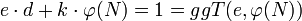 $e \cdot d + k \cdot \varphi(N) = 1 = ggT(e,\varphi(N))$
   bzw. im konkreten Beispiel: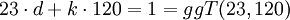 $23 \cdot d + k \cdot 120 = 1 = ggT(23,120)$
   Mit dem erweiterten euklidischen Algorithmus berechnet man nun die Faktoren d = 47 und k = − 9, so dass die Gleichung aus dem Beispiel wie folgt aussieht: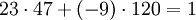 $23 \cdot 47 + (-9 )\cdot 120 = 1$
   d ist der private Schlüssel, während k nicht weiter benötigt wird.

Alternativer privater Schlüssel

Gewöhnlich wird in der Praxis der private Schlüssel etwas ausführlicher gespeichert, da diese Form der Speicherung das Entschlüsseln von Krypttexten effizienter macht (mit Hilfe des Chinesischen Restsatzes). Der private Schlüssel besteht daher dann, im Gegensatz zu dem, was im Rest dieses Artikels angenommen wird, aus folgenden Komponenten:

• N, der RSA-Modul,
• e, der Verschlüsselungsexponent,
• p, die erste Primzahl,
• q, die zweite Primzahl,
• dmod (p − 1), häufig dmp1 genannt,
• dmod (q − 1), häufig dmq1 genannt und
• (1 / q)mod p, häufig iqmp genannt.

Verschlüsseln von Nachrichten

Verschlüsselung

Um eine Nachricht K zu verschlüsseln, verwendet der Absender die Formel

$C = K^e \mod N$

und erhält so aus dem Klartext K den Geheimtext C.

Beispiel

Es soll die Zahl 7 verschlüsselt werden. Der Nachrichtenabsender benutzt den veröffentlichten Schlüssel N = 143, e = 23 und rechnet

$C \equiv 7^{23} \mod 143$

Zur Berechnung von 7²³mod 143 kann die Kongruenzarithmetik verwendet werden. Mit Hilfe der modularen Exponentiation berechnet man schnell:

$7^{23} \ \bmod \ 143 \ = \ \left(\left(\left( 7^2 \right)^2\cdot 7\right)^2\cdot 7\right)^2\cdot 7 \ \bmod \ 143 = 2$

Dabei wendet man nach jedem Rechenschritt auf die zu handhabenden Zahlen die Modulo-Operation (kurz: mod) an, um die Ergebnisse möglichst „klein“ zu halten. Aus dem Klartext 7 haben wir somit den Geheimtext 2 erhalten.

Entschlüsseln von Nachrichten (Decodierung)

Entschlüsselung

Der Geheimtext C kann durch modulare Exponentiation wieder zum Klartext K entschlüsselt werden. Der Empfänger benutzt die Formel

$K \equiv C^d \mod N$

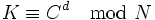
mit dem nur ihm bekannten Wert d sowie N.

Beispiel

$K \equiv 2^{47} \ \bmod\ 143 = ((((2^2)^2 \cdot 2)^2 \cdot 2)^2 \cdot 2)^2 \cdot 2 \ \bmod\ 143 = 7$

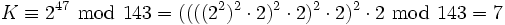
Aus C = 2 wird also wieder K = 7.

Siehe auch: Schnelles Potenzieren

Signieren von Nachrichten

Um eine Nachricht K zu signieren, wird diese vom Sender mit dem eigenen privaten Schlüssel verschlüsselt. Zum Prüfen entschlüsselt der Empfänger die Nachricht mit dem öffentlichen Schlüssel des Senders und vergleicht diese mit der zusätzlich übermittelten unverschlüsselten Nachricht K. Wenn sie übereinstimmen, ist die Signatur gültig und der Empfänger kann sicher sein, dass derjenige, der das Dokument signiert hat, auch den privaten Schlüssel besitzt und dass niemand seit der Signierung das Dokument geändert hat. Es wird also die Integrität und Authentizität garantiert, vorausgesetzt der private Schlüssel ist wirklich geheim geblieben.

Da asymmetrische Verfahren nicht geeignet sind, um größere Datenmengen zu verarbeiten, wird in der Praxis nicht die Nachricht selbst mit dem privaten Schlüssel verschlüsselt. Stattdessen wird der Hash-Wert H der Nachricht berechnet. Dieser bildet dann (meist zusammen mit einigen technisch notwendigen Informationen, wie zum Beispiel der Spezifizierung des verwendeten Hashverfahrens) die Eingabe K ^* für eine Verschlüsselung mit dem privaten Schlüssel, deren Resultat dann die eigentliche Signatur ist. Der Empfänger kann die so erhaltene Signatur mit dem öffentlichen Schlüssel entschlüsseln und erhält so K ^* und somit den Hash-Wert H der ursprünglichen Nachricht. Anschließend kann er selber den Hash-Wert H₁ der ihm vorgelegten Nachricht bestimmen und mit dem in K ^* gespeicherten Hash-Wert H vergleichen. Wenn die beiden Hash-Werte übereinstimmen, kann mit hoher Wahrscheinlichkeit davon ausgegangen werden, dass die Nachricht fehlerfrei übertragen wurde und nicht gefälscht ist.

Siehe auch: Elektronische Unterschrift, Full-Domain-Hash

Sicherheit

Public-Key Verschlüsselungs-Verfahren wie RSA werden in der Praxis immer als hybride Verfahren in Verbindung mit symmetrischen Verfahren verwendet. Bei der Analyse der Sicherheit müssen die Sicherheit des Public-Key-Verfahrens und die praktische Sicherheit des Gesamtsystems betrachtet werden.

Sicherheit von RSA

Bei der Kryptanalyse des RSA-Verfahrens unterscheidet man zwischen zwei Problemen:

• RSA-Problem (RSAP): Gegeben sind der öffentliche Schlüssel (N,e) sowie der Geheimtext C. Gesucht wird der Klartext K wobei gilt: $K^e\equiv C\pmod{N}$

Das Problem liegt hier in der Schwierigkeit Wurzeln modulo N zu ziehen, was zur Bestimmung des Klartexts K notwendig ist.

• RSA-Schlüsselproblem (RSAP ^* ): Gegeben ist der öffentliche Schlüssel (N,e). Gesucht wird der geheime Schlüssel d wobei gilt: $ed\equiv 1\pmod{\varphi(N)}$

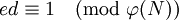
Das Problem liegt hier in der Schwierigkeit die Eulersche φ-Funktion von N ohne Kenntnis der Faktoren p und q zu berechnen.

Folgende Beziehungen zwischen den RSA-Problemen und FACTORING, dem Faktorisierungsproblem, sind bekannt:

$\mathrm{RSAP} \leq_p \mathrm{RSAP^*} =_p \mathrm{FACTORING}$

Die Beziehung 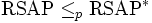$\mathrm{RSAP} \leq_p \mathrm{RSAP^*}$ ist trivial, denn wenn man den privaten Schlüssel hat, kann man damit wie oben jeden beliebigen Geheimtext entschlüsseln. Ob die Umkehrung gilt, ist zurzeit unbekannt.

Auch die Beziehung 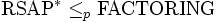$\mathrm{RSAP^*} \leq_p \mathrm{FACTORING}$ ist trivial, denn wenn man N = pq faktorisiert hat, kann man damit leicht 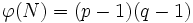$\varphi(N)=(p-1)(q-1)$ berechnen, und dann mit dem euklidischen Algorithmus zu gegebenem öffentlichen Schlüssel den zugehörigen privaten Schlüssel effizient berechnen, wie in der Schlüsselerzeugung.

Für die Beziehung 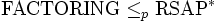$\mathrm{FACTORING} \leq_p \mathrm{RSAP^*}$ ist schon lange ein probabilistischer Polynomialzeitalgorithmus bekannt. Vor kurzem wurde gezeigt, dass sich diese Reduktion im balancierten RSA (d.h. p und q haben gleiche Bitlänge) auch deterministisch durchführen lässt. Der Beweis verwendet das Coppersmith-Verfahren zur Bestimmung von Nullstellen eines irreduziblen bivariaten Polynoms mit ganzzahligen Koeffizienten, welches sich auf eine Gitterreduktion zurückführen lässt.

Da alle gängigen Implementierungen balanciertes RSA verwenden, ist in der Praxis das Brechen des geheimen Schlüssels nur mit der Kenntnis des öffentlichen Schlüssels genau so schwer wie das Faktorisieren von N. Wegen 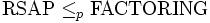$\mathrm{RSAP} \leq_p \mathrm{FACTORING}$ ist im Fall der zusätzlichen Kenntnis eines Geheimtexts die Schwierigkeit des Faktorisierungsproblems von zentralem Interesse.

Man möchte N = pq für sehr große Primzahlen p und q faktorisieren. Diese Primfaktorzerlegung ist für große Zahlen mit den heute bekannten Verfahren praktisch nicht durchführbar. Es ist aber nicht bewiesen, dass es sich bei der Primfaktorzerlegung um ein prinzipiell schwieriges Problem handelt.

Mit dem Quadratischen Sieb wurde 1994 die Zahl RSA-129 mit 129 Dezimal-Stellen in 8 Monaten von ca. 600 Freiwilligen faktorisiert. Mit der Methode des Zahlkörpersiebs wurde im Jahr 2005 von Wissenschaftlern der Universität Bonn die im Rahmen der RSA Factoring Challenge von RSA Laboratories vorgegebene 200-stellige Dezimalzahl RSA-200 in ihre zwei großen Primfaktoren zerlegt. Die Faktorisierung begann Ende 2003 und dauerte bis Mai 2005. Unter anderem kam ein Rechnerverbund von 80 handelsüblichen Rechnern an der Universität Bonn zum Einsatz. Im November 2005 zahlten RSA Laboratories für die Faktorisierung von RSA-640, einer Zahl mit 640 Bits bzw. 193 Dezimalstellen, eine Prämie von 20.000 US-Dollar. Mittlerweile wurde das RSA Factoring Challenge beendet.

Für die Faktorisierung von RSA-1024 (309 Dezimalstellen) oder gar RSA-2048 (617 Dezimalstellen) waren 100.000 $ bzw. 200.000 $ ausgelobt; die RSA Laboratories haben im Mai 2007 das RSA Factoring Challenge beendet, nachdem die o.g. Wissenschaftler der Universität Bonn im selben Monat eine 1039-Bit Zahl (312 Dezimalstellen) faktorisiert haben.^[3] Die wachsende Rechenleistung moderner Computer stellt für die kurzfristige Sicherheit von RSA im Wesentlichen kein Problem dar, zumal diese Entwicklung vorhersehbar ist: Der Nutzer kann bei der Erzeugung seines Schlüssels darauf achten, dass er während der Dauer der beabsichtigten Verwendung nicht faktorisiert werden kann. Nicht vorhersehbare Entwicklungen, wie die Entwicklung deutlich schnellerer Algorithmen oder gar eines leistungsfähigen Quantencomputers bergen zumindest für die mittel- und langfristige Sicherheit der verschlüsselten Daten gewisse Risiken.

In einigen Spezialfällen kann man das RSA-Verfahren brechen, ohne das Faktorisierungsproblem gelöst zu haben. Der Angriff von Wiener bei balanciertem RSA löst das RSA-Schlüsselproblem effizient unter der Annahme, dass der private Schlüssel nur eine geringe Bitlänge aufweist, genauer $d&amp;amp;lt;\frac{\sqrt[4]{N}}{3}$. Wiener verwendete dabei die Tatsache, dass unter der Abschätzung für d der Bruch 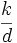$\frac{k}{d}$ (für eine ganze Zahl k) in der Kettenbruchentwicklung von 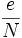$\frac{e}{N}$ auftaucht. Die Schranke wurde mit Mitteln der Gitterreduktion auf d < N^0.292 verbessert.

Auch das RSA-Problem kann unter einigen Annahmen effizient ohne Faktorisieren gelöst werden. Der Angriff von Håstad ermittelt einen Klartext, der mit kleinem Verschlüsselungsexponent (etwa e = 3) für mehrere Empfänger vor dem Verschlüsseln speziell aufbereitet wurde, etwa wenn die Nummer des Empfängers in den Klartext codiert wurde. Dieser Angriff verwendet die Coppersmith-Methode, um kleine Nullstellen eines Polynoms in einer Unbestimmten zu berechnen, welche wiederum auf Gitterreduktion basiert.

Praktische Sicherheit

Da die RSA-Funktion x→x^dmod n multiplikativ ist (d. h. (xy)^d = x^dy^dmod n gilt), lassen sich aus bekannten Klartexten 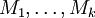$M_1, \ldots,M_k$ von Chiffretexten 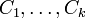$C_1, \ldots, C_k$ zu einem Chiffretext C, der sich als Produkt

$C=\prod C(M_i)^{e_i}\bmod n$

mit ganzzahligen e_i darstellen lässt, der Klartext M als

$M=\prod M_i^{e_i}\bmod n$

berechnen. Analog dazu lässt sich aus bekannten (echten) Signaturen 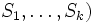$S_1,\ldots,S_k)$ zu Nachrichten 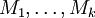$M_1, \ldots,M_k$ weitere (gefälschte) Signaturen

$S(M)=\prod S_i^{e_i}\bmod n$

berechnen. Da bei digitalen Signaturen in der Regel nur Hashwerte signiert werden, ist der Angriff dann erfolgreich, wenn diese multiplikative Relation auch für die Hash-Werte der Nachrichten M und 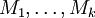$M_1, \ldots,M_k$ gilt.

Um solche Angriffe zu verhindern, werden bei RSA-Verschlüsselung und RSA-Signatur so genannte Padding-Verfahren eingesetzt. Diese nutzen aus, dass die Länge des Klartextes bzw. Hash-Wertes deutlich kleiner als die Länge von n ist, und fügen dem Klartext bzw. dem Hash-Wert vor der Verschlüsselung oder Signatur einen String R mit vorgegebener Struktur (d. h. mit Redundanz) an. Es wird also die RSA-Funktion nicht auf die Nachricht M oder auf den Hash-Wert h(M) angewendet, sondern auf M|R bzw. h(M)| R, wobei „|“ eine Konkatenation bezeichnet. In der Regel enthält R eine Angabe über die Länge der Nachricht oder des Hash-Wertes oder eine eindeutige Zeichenfolge, die den Beginn von R kennzeichnet. Dies erleichtert nicht nur die Dekodierung, sondern erschwert auch Angriffe. Padding-Verfahren können für die Berechnung von R auch Zufallszahlen und Hashfunktionen verwenden. Standards für Padding-Verfahren für RSA werden z. B. in PKCS#1 oder ISO 9796 definiert. Einige moderne Paddingverfahren – beispielsweise das Optimal Asymmetric Encryption Padding (OAEP) oder das Probabilistic Signature Scheme (PSS) – verwenden kryptographische Hashfunktionen und sind (unter idealisierten Annahmen) beweisbar ebenso schwierig zu brechen, wie RSA selbst.^{[4] [5]}

RSA wird in der Regel in Hybridverfahren mit symmetrischen Verschlüsselungsverfahren kombiniert. Dabei wird zufällig ein Sitzungsschlüssel für eine symmetrische Verschlüsselung generiert, der dann per RSA verschlüsselt und zusammen mit der Nachricht übertragen wird.

Bei der Signatur wird nicht die gesamte Nachricht, sondern nur ein Hash-Wert signiert. Der symmetrische Schlüssel bzw. der Hash-Wert sind dabei relativ kurz. Für den symmetrischen Schlüssel gilt also

$K_{sym} &amp;amp;lt; N = p\cdot q$.

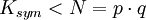Daher kann der symmetrische Schlüssel mit einer einzigen RSA-Verschlüsselung verschlüsselt werden. Für die Sicherheit von RSA sind Primzahlen mit über 100 Stellen erforderlich. Daher könnte ein symmetrischer Schlüssel mit über 200 Stellen verschlüsselt werden.

Als sehr sicher eingestufte Algorithmen zur symmetrischen Verschlüsselung gelten 3DES und AES. Diese verwenden 112, 128, 168 oder maximal 256 Bit. Dies entspricht bei 256 Bit etwa 77 Dezimalstellen. Damit ist ein Brute-Force-Angriff faktisch auszuschließen. Eine sichere Hashfunktion wie SHA-256 erzeugt Funktionswerte mit einer Länge von ebenfalls 256 Bit. Damit lassen sich Signaturverfahren mittels RSA realisieren, die nur einen Verschlüsselungsschritt benötigen.

Die Sicherheit und die Performance des Gesamtsystems werden durch die Sicherheit des Public-Key-Verfahrens limitiert, sofern nur als sicher eingestufte Algorithmen verwendet werden und die Wahl des Schlüssel als hinreichend zufällig betrachtet werden kann.

RSA ist kein Primzahltest

Wenn p und q Primzahlen sind, funktioniert das RSA-Verfahren. Umgekehrt kann aber aus dem funktionierenden RSA-Verfahren nicht geschlossen werden, dass p und q Primzahlen sind, denn bei Carmichael-Zahlen funktioniert das Verfahren, obwohl Carmichael-Zahlen keine Primzahlen sind.

Vollständiges Beispiel

Vorarbeiten

Die oben genannten Schritte sollen nun an einem vollständigen Beispiel erläutert werden. Um einen Text zu verschlüsseln, müssen zunächst Buchstaben in Zahlen umgewandelt werden. Dazu verwendet man in der Praxis zum Beispiel den ASCII-Code. Hier sei willkürlich die folgende Zuordnung gewählt:

A=01 B=02 C=03 usw. (00 = Leerzeichen)

Darüber hinaus sei angenommen, dass jeweils drei Zeichen zu einer Zahl zusammengefasst werden. Die Buchstabenfolge AXT wird also zu 012420. Die kleinste zu verschlüsselnde Zahl ist dann 000000 (drei Leerzeichen), die größte 262626 (ZZZ). Der Modulus 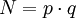$N = p \cdot q$ muss also größer 262626 sein.

Klartext:  W I K  I P E  D I A
Kodierung: 230911 091605 040901

Schlüsselerzeugung

Zunächst werden geheim zwei Primzahlen gewählt, beispielsweise p = 307 und q = 859. Damit ergibt sich:

$N = p \cdot q = 263713$

$\varphi(N) = (p-1) \cdot (q-1) = 262548$

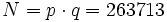
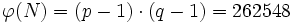
e = 1721 (zufällig, teilerfremd zu $\varphi(N)$)

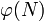d = 1373 (das multiplikative Inverse zu 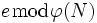$e \bmod \varphi(N)$ mit Hilfe des Erweiterten euklidischen Algorithmus)

Öffentlicher Schlüssel: e = 1721 und N = 263713

Geheimer Schlüssel: d = 1373 und N = 263713

Verschlüsselung

Cn = Kne mod N   für n=1,2,3(,...)
C1 = 2309111721 mod 263713 = 001715
C2 = 0916051721 mod 263713 = 184304
C3 = 0409011721 mod 263713 = 219983

Entschlüsselung

Kn = Cnd mod N   für n=1,2,3(,...)
K1 = 0017151373 mod 263713 = 230911
K2 = 1843041373 mod 263713 = 091605
K3 = 2199831373 mod 263713 = 040901

Signatur (Verschlüsselung mit dem geheimen Schlüssel)

Cn = Knd mod N
C1 = 2309111373 mod 263713 = 219611
C2 = 0916051373 mod 263713 = 121243
C3 = 0409011373 mod 263713 = 138570

Verifikation (Entschlüsselung mit dem öffentlichen Schlüssel)

Kn = Cne mod N
K1 = 2196111721 mod 263713 = 230911
K2 = 1212431721 mod 263713 = 091605
K3 = 1385701721 mod 263713 = 040901

Anwendungsgebiete

• Internet- und Telefonie-Infrastruktur: X.509-Zertifikate
• Übertragungs-Protokolle: IPSec, TLS, SSH, WASTE
• E-Mail-Verschlüsselung: PGP, S/MIME
• Authentifizierung französischer Telefonkarten
• Kartenzahlung: EMV

Literatur

• Der Dialog der Schwestern. In: c’t. Nr. 25, 1999 (Liegt auch dem E-Learning-Programm CrypTool bei). 
• Alexander May: Computing the RSA Secret Key is Deterministic Polynomial Time Equivalent to Factoring. In: Advances in Cryptology (Crypto 2004), Lecture Notes in Computer Science. Band 3152, Springer Verlag, 2004, S. 213–219. 
• Dan Boneh: Twenty Years of Attacks on the RSA Cryptosystem. In: Notices of the American Mathematical Society (AMS). Band 46, Nr. 2, 1999, S. 203–213. 

Weblinks

• RSA-Paper von Rivest, Shamir und Adleman
• Übersicht über erfolgreiche Faktorisierungen im RSA-Wettbewerb
• Erklärung von RSA vom Fachbereich Mathematik der Universität Wuppertal
• Bekannte Attacken auf RSA-Verfahren (in englischer Sprache)
• Zahlentheoretische Arbeit über RSA
• Faktorisierung von RSA-200
• Arbeit über RSA mit Schwerpunkt in der Informatik
• RSA-Codebeispiel in Scheme vom Massachusetts Institute of Technology

Einzelnachweise

1. ↑ D. Boneh: Twenty Years of Attacks on the RSA Cryptosystem. In: Notes of the AMS. 46, Nr. 2, Februar 1999, S. 203–213 (PDF). 
2. ↑ MJ Wiener: Cryptanalysis of short RSA secret exponents. In: IEEE Transactions on information theory. 36, Nr. 3, Mai 1990, S. 553–558 (doi:10.1109/18.54902). 
3. ↑ http://www.crypto-world.com/announcements/m1039.txt
4. ↑ What is OAEP? (englisch)
5. ↑ What is PSS/PSS-R? (englisch)