Ramseypreis

Ramsey-Preise (nach Frank Plumpton Ramsey) zielt die zweitbeste (second best) Lösung bei der Regulierung eines natürlichen Monopols an. Natürliche Monopole entstehen in erster Linie dann, wenn hohe Fixkosten, aber vergleichsweise geringe variable Kosten für die Produktion bzw. das Angebot eines Produktes oder einer Dienstleistung entstehen, also stetig fallende Durchschnittskosten im für die Produktion relevanten Bereich vorherrschen.

Ein Beispiel dafür ist der Telekommunikationsbereich. Ein einziger großer Anbieter kann dabei zumindest im Festnetzbereich weitaus kosteneffizienter arbeiten als mehrere kleine Anbieter. Grund dafür sind versunkene Kosten. Als solche werden - in diesem Fall - die Kosten für die vergrabenen Telefonleitungen angesehen. Die Kosten für diese Leitungen können nicht mehr rückgängig gemacht und die Leitungen auch keinem völlig anderen Zweck gewidmet werden. Ein unreguliertes Monopol führt in der Regel jedoch zu hohen Preisen (der Monopolist maximiert seine Gewinne), die aus Sicht der Wohlfahrtstheorie nicht optimal und politisch meistens auch nicht gewünscht sind. Generell ist es wohlfahrtsoptimierend, wenn der Preis den Grenzkosten entspricht (first best Lösung). Wenn die Durchschnittskosten jedoch über den Grenzkosten liegen, kann ein Unternehmen nicht kostendeckend arbeiten. Möglichkeiten, die first best Lösung zu erreichen, wären die Verstaatlichung des Unternehmens oder Subventionen. Die Subventionen würden dann in der Höhe der Differenz zwischen Durchschnittskosten und den Grenzkosten ausfallen. Hierfür müssten aber die Kostenfunktionen des Unternehmens bekannt sein, was sie i. d. R. aber nicht sind. Subventionen setzen zudem häufig falsche Anreize (Verschwendung) oder sind politisch nicht durchsetzbar. Hierzu existieren eine Fülle von Theorien zu sog. bayesschen und nicht-bayesschen Subventionsverfahren.

Generell lautet das Problem: Optimierung der Wohlfahrt unter der Bedingung, dass das Unternehmen kostendeckend arbeitet. Im Ein-Güter-Fall, also wenn das Unternehmen nur ein homogenes Gut anbietet, besteht die second-best Lösung darin, den Preis mit den Durchschnittskosten gleichzusetzen. Bietet das Unternehmen mehrere verschiedene Güter an (etwa: Orts- und Ferngespräche) bzw. bedient verschiedene Nachfrager (etwa: Gewerbe- und Privatkunden), so ergibt sich als Ergebnis der Optimierung

$\frac{p_i - GK}{p_i} = \frac{k}{\eta_i}$

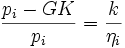
wobei p_i den Preis des Gutes i, GK die Grenzkosten, und η_i die Preiselastizität der Nachfragegruppe i bezeichnet. k ist gleich

$\frac{1 - \lambda}{\lambda} = konstant$

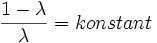
wobei sich λ aus der Optimierung ergibt (Lagrange-Parameter). Das Ergebnis macht deutlich, dass die Ramsey-Regel nur die Preisstruktur bestimmt. Die Konstante muss so gesetzt werden, dass die Gewinnrestriktion (Kostendeckung) erfüllt ist.

Der relative Zuschlag auf die Grenzkosten ist also umgekehrt proportional zur Preiselastizität. Dementsprechend zahlen die, die am schlechtesten ausweichen (verzichten oder substituieren) können, die höchsten Preise. Dieses Verfahren wird auch als Quersubventionierung bezeichnet - das weniger preiselastische Gut subventioniert die Kosten des Unternehmens gegenüber dem preiselastischeren Gut.

Herleitung

Es gilt, die aggregierte Konsumentenrente der Nachfragefunktionen

$KR: \sum_i \int_{p_i}^{\infty} x_i(\tilde{p}_i)d\tilde{p}_i$

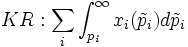
unter der Nebenbedingung, dass das Unternehmen kostendeckend arbeitet

$s.t. \sum_i p_ix_i(p_i)-C\left(\sum_i x_i(p_i)\right) = 0$

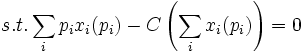
zu optimieren.

$\mathcal{L} = \sum_i \int_{p_i}^{\infty} x_i(\tilde{p}_i)d\tilde{p}_i +\lambda\left[\sum_i p_ix_i(p_i)-C\left(\sum_i x_i(p_i)\right)\right]$

$\frac{\partial \mathcal{L}}{\partial p_i} = -x_i(p_i) + \lambda\left[x_i(p_i) + p_i x'_i(p_i) - C'x'\right] = 0$

$\Leftrightarrow \frac{\frac{dx_i}{dp_i}(p_i - GK)}{x_i} = \frac{1-\lambda}{\lambda}$

$\Leftrightarrow \frac{p_i - GK}{p_i} = \frac{k}{\frac{dx_i}{dp_i}*\frac{p_i}{x_i}} = \frac{k}{\eta_{x_i,p_i}}$

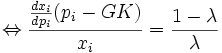
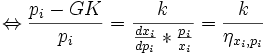
Siehe auch

• Höchstpreisregulierung