Randbedingungen

Randbedingungen sind im Allgemeinen die Umstände, die nur mit großem Aufwand oder gar nicht beeinflussbar sind und daher als gegebene Größen verwendet werden müssen.

Randbedingungen und Differentialgleichungen

Im Bereich der Differentialgleichungen sind Randbedingungen konkrete Angaben zum Berechnen der Lösungsfunktion u auf einer Definitionsmenge D. Dazu werden die Werte der Funktion auf dem Rand (im topologischen Sinn) des gewünschten Definitionsbereichs D vorgegeben. Im einfachsten Fall ist D = (a,b) ein Intervall und die Randbedingungen sind vorgegebene Funktionswerte 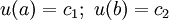$u(a)=c_1;\;u(b)=c_2$. Werden hier statt zwei Werten nur an einem Randpunkt des Intervalles – meistens a – Werte für u und zusätzlich für Ableitungen von u vorgegeben, spricht man von einem Anfangswertproblem und nennt die vorgegebenen Werte seine Anfangsbedingungen.

Bei partiellen Differentialgleichungen betrachtet man die Differentialgleichung meistens auf Sobolew-Räumen. In diesen Räumen werden Funktionen, die bis auf Nullmengen übereinstimmen, als gleich angesehen. Da der Rand eines Gebietes üblicherweise eine Nullmenge ist, ist der Begriff der Randbedingung problematisch. Lösungen für dieses Problem sind sobolewsche Einbettungssätze oder - allgemeiner - Spuroperatoren.

Randwertaufgaben haben nicht immer eine Lösung (siehe Beispiel), im Falle ihrer Existenz ist die Lösung nicht in allen Fällen eindeutig. Die Berechnung einer Näherungslösung für eine Randwertaufgabe mit Mitteln der numerischen Mathematik ist oft aufwändig und läuft meist auf die Lösung sehr großer Gleichungssysteme hinaus.

Beispiel

Sei die gegebene Differentialgleichung y''(x) = − y(x). Die Lösungsmenge dieser Gleichung ist asin(x) + bcos(x).

• Gesucht ist die Lösung mit y(0) = 1 und y(π / 2) = 0. $\Rightarrow$ Die Lösung ist y = cos(x).

• Gesucht ist die Lösung mit y(0) = 0 und y(π) = 0. $\Rightarrow$ Es gibt unendlich viele Lösungen der Form asin(x) mit beliebigem a.

• Gesucht ist die Lösung mit y(0) = 0 und y(2π) = 1. $\Rightarrow$Es gibt keine Lösung.

Arten von Randbedingungen

Es gibt unterschiedliche Möglichkeiten, auf dem Rand des betrachteten Gebietes Werte vorzuschreiben. Eine Möglichkeit ist es, Werte der Lösung vorzuschreiben, dann spricht man von Dirichlet-Randbedingungen. Auf der anderen Seite kann man Bedingungen an die Ableitungen stellen, dann spricht man von Neumann-Randbedingungen (bei gewöhnlichen Differentialgleichungen, wie oben ausgeführt, von Anfangsbedingungen).

Künstliche Randbedingungen

Bei unbeschränkten Gebieten erfordert die numerische Lösung üblicherweise eine Einschränkung des Gebiets. Hier sind dann Randbedingungen vorzugeben, die im eigentlichen Problem nicht vorhanden, also künstlich sind.

Siehe auch

• Nebenbedingung