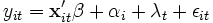- Random-Effects-Modell
-
Inhaltsverzeichnis
Abgrenzung statische und dynamische Modelle
Paneldaten entstehen durch wiederholte Querschnittserhebungen an denselben Individuen, sogenannten Panelstudien. Dadurch werden sowohl dynamische Aspekte (wie entwickelt sich ein Merkmal im Zeitablauf?) als auch die Heterogenität der Individuen berücksichtigt. Außerdem kann man abhängig vom gewählten Modell zwischen Kohorten-, Perioden- und Alterseffekten unterscheiden. Durch die Menge an Beobachtungen steigt die Zahl der Freiheitsgrade und sinkt die Kollinearität, sodass die Schätzer effizienter werden. Im Vergleich zu mehreren, unabhängigen Querschnittsregressionen führen Paneldaten bei der Schätzung exogener Variablen zu besseren Ergebnissen. Durch die Verwendung einer individuenspezifischen Konstante kann der Einfluss konstanter, nicht modellierter Variablen eingefangen werden; dadurch werden die Schätzer robuster gegenüber unvollständiger Modellspezifikation. Man unterscheidet zwischen balancierten und unbalancierten Daten. Erstere stellen einen idealtypischen Datensatz dar, bei dem für alle Individuen alle Daten für alle Zeitpunkte vorliegen. In der Realität sind die Daten meist unvollständig, man spricht dann von unbalancierten Panels. Die Verwendung unbalancierter Daten stellt bei den betrachteten Modellen kein Problem dar, sofern die Daten zufällig fehlen und genügend aufeinander folgende Beobachtungen vorhanden sind. Systematisch fehlende Beobachtungen führen dagegen zu einem Selektionsbias und machen spezielle Schätzverfahren notwendig. Ein weiterer Vorteil liegt in der Vergrößerung der Datenbasis.
Statische Modelle berücksichtigen die zeitliche Entwicklung der abhängigen Variable nicht. Zu ihnen zählen das gepoolte Modell, das Random-Effects- und das Fixed-Effects-Modell (RE- bzw. FE-Modell). Ihre Verwendung ist sinnvoll, wenn die Reaktion der Individuen nur von den exogenen Variablen, nicht jedoch von älteren Werten der betrachteten Größe abhängt. Im gepoolten Modell wird die Heterogenität der Beobachtungen sowohl in der Zeit als auch in der Querschnittsdimension vernachlässigt, wie im gewöhnlichen linearen Regressionsmodell werden sämtliche Koeffizienten als nichtstochastisch und identisch für alle Beobachtungen erachtet. Die Schätzer sind effizienter als bei T Querschnittsregressionen mit je N Beobachtungen, da mit steigender Zahl der Beobachtungen der Standardfehler der Koeffizienten sinkt, sofern sich diese nicht signifikant unterscheiden; Heterogenität führt jedoch zu verzerrten Schätzern. Außerdem ist fraglich, ob die Beobachtungen unabhängig sind, da dieselben Individuen wiederholt befragt werden („serial correlation“).
Im Random-Effects-, genauer Random-Intercepts- oder Error-Components-Modell, wird ein individuenspezifischer Achsenabschnitt αi eingeführt, der für jedes Individuum die Realisation einer für alle Individuen identisch verteilten Zufallsvariablen ist:
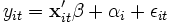 , mit
, mit 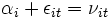 .
.
Hierbei stellt yit den Wert der zu erklärenden Variablen dar,
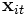 den Vektor der K erklärenden Variablen und
den Vektor der K erklärenden Variablen und 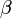 die Regressionskoeffizienten dar. Der Gesamtfehler νit setzt sich aus dem individuenspezifischen Achsenabschnitt αi und dem idiosynkratischen (zeitvariablen, systematischen) Fehler εit zusammen.
die Regressionskoeffizienten dar. Der Gesamtfehler νit setzt sich aus dem individuenspezifischen Achsenabschnitt αi und dem idiosynkratischen (zeitvariablen, systematischen) Fehler εit zusammen.Im Fixed-Effects Grundmodell hingegen variiert der Achsenabschnitt αi systematisch, während die βk weiterhin für alle Individuen gleich bleiben. Die αi sind somit zu schätzende Parameter und modellieren die Heterogenität der Individuen wie im RE-Modell nur durch eine Niveauverschiebung – also durch unterschiedliche αi. Der Einfluss der erklärenden Variablen soll für alle Individuen gleich sein. Dieses Verfahren erklärt somit, warum eine Beobachtung vom individuellen Mittelwert abweicht, nicht jedoch die Unterschiede in den (Mittel-)Werten verschiedener Individuen. Daher sind zeitkonstante Variablen im Modell mit fixen Effekten nicht identifiziert.
- Beispiele:
- die unbeobachtbaren Fähigkeiten des Managements beeinflussen die Gewinnsituation von Unternehmen
- Ausbildung beeinflusst die Gehaltsituation von Arbeitnehmern
Generell sollen Random-Effects Modelle bevorzugt werden, wenn die Charakteristika einer Grundgesamtheit aus einigen Individuen hergeleitet werden sollen. Fixed-Effects Modelle bieten sich insbesondere dann an, wenn Vorhersagen (Inferenzen) nur für die betrachtete Stichprobe getroffen werden sollen; sie sollten aber auch im obigen Fall angewendet werden, wenn αi und xit korreliert sind und das Random-Effects-Modell so zu inkonsistenten und verzerrten Schätzern führt. Ein Argument gegen FE-Modelle ist der Verlust an Freiheitsgraden, da mit jedem Individuum eine neue Variable geschätzt werden muss. Wenn die Varianz der Werte eines Individuums (Within-Varianz) sehr viel geringer ist als die Varianz zwischen den Individuen (Between-Varianz), ist das FE-Modell nachteilig: Man ignoriert einen Teil der Information und unterstellt, dass die Mittelwerte von x und y nichts über die Beziehung der Variablen aussagen.Das two-way model (die deutsche Übersetzung "zweistufiges Modell" ist leicht verwirrend)
basiert zwar auf statischen Verfahren, bildet aber durch die für alle Individuen geltende, aber zeitabhängige Variable λt Niveauunterschiede in den verschiedenen Perioden ab. λt kann analog zu αi im Rahmen eines FE- oder RE-Modells geschätzt werden. Da die zeitabhängige Konstante für jede Periode neu festgelegt werden muss, ist dieses Modell zur Prognose nicht geeignet.
Eine weitere Möglichkeit, Veränderungen im Zeitablauf zu berücksichtigen, liegt in der Verwendung so genannter verteilter Lag-Modelle, die die Wirkung einer veränderten unabhängigen Variable auf die erklärte Variable über einen unendlich großen Zeithorizont verteilt. Eine solche Konstruktion erklärt somit verzögerte Wirkungen aus psychologischen, technologischen oder institutionellen Gründen. In diesen Modellen muss insbesondere der Multikollinearität besondere Beachtung geschenkt werden. Außerdem treten Probleme durch die Wahl der richtigen Anzahl verzögerter Beobachtungen und ein Verlust an Beobachtungswerten auf: Bei steigender Zahl der Parameter sinkt die Zahl der verfügbaren Beobachtungen.
Dynamische Modelle enthalten implizit über den Fehlerterm εit = ρεi,t − 1 + / zetait (autoregressive Modelle) oder explizit (LDV = „lagged dependent variable“) eine verzögerte endogene Variable (also bspw. yi,t − 1, wenn yiterklärt werden soll). Dieser Ansatz implementiert die intuitiv einleuchtende Vorstellung, dass das Niveau einer Vorjahresgröße eine primitive Prognose für die aktuelle Größe darstellt. Das dynamische LDV-Modell lautet:
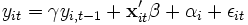 , mit
, mit 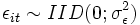 .
.
Der Koeffizient γ kann nicht kausal (wie im statischen Modell) interpretiert werden, sondern beschreibt die Anpassungsgeschwindigkeit des dynamischen Effekts.
Schätzverfahren in den statischen Modellen
Bei statischen Modellen werden die KQ-Methode (gepooltes Modell), der LSDV-Schätzer (least squares dummy variable im Fixed-Effects-Modell) und der FGLS-Schätzer (Feasible Generalized Least Squares im Random-Effects-Modell) verwendet.
Schätzverfahren in den dynamischen Modellen
Bei dynamischen Modellen hängt die zeitverzögerte endogene Variable von αi ab, da die auf Individuenmittelwerte transformierten Fehlerterme und verzögerten Variablen miteinander korreliert sind – dies gilt unabhängig davon, ob die αi als fix oder zufällig angesehen werden. Daher sind KQ-Schätzer bei endlichen Zeithorizonten T verzerrt und nicht konsistent; selbst für T=30 sind die Verzerrungen noch sehr deutlich, für
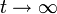 beträgt die asymptotische Verzerrung O(T − 1). Dieses Landau-Symbol besagt vereinfachend, dass die Verzerrung höchstens so schnell sinkt wie 1/T. Eine Alternative bieten daher bestimmte GMM-Schätzer (generalized method of moments), ein Oberbegriff für viele lineare und nichtlineare Schätzverfahren einschließlich OLS und den nun zu diskutierenden Instrumentvariablen (IV). Solche Verfahren erfordern keine Annahmen über die Verteilung der Fehlerterme, erlauben Heteroskedastizität und können (numerisch) selbst dann gelöst werden, wenn eine analytische Lösung nicht möglich ist. IV-Schätzer führen bei Korrelation der erklärenden Variablen mit dem Fehlerterm zu konsistenten Schätzern, soweit keine anderen Bedingungen verletzt sind. Diese Korrelation kann wie hier durch endogene Variablen, aber auch durch unberücksichtigte erklärende Variablen, Selbstselektion (Individuen nehmen nur bei ihrer Meinung nach positiven Umständen an der Umfrage teil) oder durch Messfehler verursacht sein. Bei der IV-Methode wird die Korrelation zwischen yi,t − 1 und εit zumindest asymptotisch eliminiert, indem man yi,t − 1 durch Größen ersetzt, die zwar in engem Zusammenhang mit yi,t − 1 stehen (also relevant sind), aber nicht mit εit korrelieren oder eine Linearkombination anderer erklärender Variablen darstellen und somit gültig sind. Wenn die Anzahl R der Instrumente der Anzahl K der erklärenden Variablen entspricht, so spricht man vom IV-Modell (hierbei können exogene Variablen ihre eigenen Instrumente sein), gilt R>K, so ist das Modell überidentifiziert und man erhält den effizienteren, in endlichen Stichproben aber möglicherweise stärker verzerrten GIVE, den „generalized instrumental variables estimator“. Der Schätzer im Fall R=K lautet
beträgt die asymptotische Verzerrung O(T − 1). Dieses Landau-Symbol besagt vereinfachend, dass die Verzerrung höchstens so schnell sinkt wie 1/T. Eine Alternative bieten daher bestimmte GMM-Schätzer (generalized method of moments), ein Oberbegriff für viele lineare und nichtlineare Schätzverfahren einschließlich OLS und den nun zu diskutierenden Instrumentvariablen (IV). Solche Verfahren erfordern keine Annahmen über die Verteilung der Fehlerterme, erlauben Heteroskedastizität und können (numerisch) selbst dann gelöst werden, wenn eine analytische Lösung nicht möglich ist. IV-Schätzer führen bei Korrelation der erklärenden Variablen mit dem Fehlerterm zu konsistenten Schätzern, soweit keine anderen Bedingungen verletzt sind. Diese Korrelation kann wie hier durch endogene Variablen, aber auch durch unberücksichtigte erklärende Variablen, Selbstselektion (Individuen nehmen nur bei ihrer Meinung nach positiven Umständen an der Umfrage teil) oder durch Messfehler verursacht sein. Bei der IV-Methode wird die Korrelation zwischen yi,t − 1 und εit zumindest asymptotisch eliminiert, indem man yi,t − 1 durch Größen ersetzt, die zwar in engem Zusammenhang mit yi,t − 1 stehen (also relevant sind), aber nicht mit εit korrelieren oder eine Linearkombination anderer erklärender Variablen darstellen und somit gültig sind. Wenn die Anzahl R der Instrumente der Anzahl K der erklärenden Variablen entspricht, so spricht man vom IV-Modell (hierbei können exogene Variablen ihre eigenen Instrumente sein), gilt R>K, so ist das Modell überidentifiziert und man erhält den effizienteren, in endlichen Stichproben aber möglicherweise stärker verzerrten GIVE, den „generalized instrumental variables estimator“. Der Schätzer im Fall R=K lautet 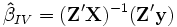 , wobei
, wobei 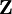 die
die  -Matrix der verfügbaren Instrumente ist. Diese Gleichung lässt sich auch aus dem GIVE für R>K herleiten:
-Matrix der verfügbaren Instrumente ist. Diese Gleichung lässt sich auch aus dem GIVE für R>K herleiten: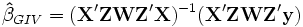 , falls
, falls 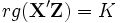 .
.
Dieser Schätzer resultiert aus der Minimierung einer quadratischen Funktion der Stichprobenmomente. Sofern die
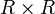 -Gewichtungsmatrix
-Gewichtungsmatrix 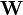 positiv definit ist, werden die Schätzer konsistent sein, da die zu minimierende quadratische Gleichung nur positive Werte annehmen kann und bei steigendem N gegen Null strebt. Da jedes skalare Vielfache der inversen Kovarianzmatrix der Stichprobenmomente zu effizienten Schätzern führt, ergibt sich unter der Annahme
positiv definit ist, werden die Schätzer konsistent sein, da die zu minimierende quadratische Gleichung nur positive Werte annehmen kann und bei steigendem N gegen Null strebt. Da jedes skalare Vielfache der inversen Kovarianzmatrix der Stichprobenmomente zu effizienten Schätzern führt, ergibt sich unter der Annahme 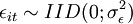 die optimale Gewichtungsmatrix:
die optimale Gewichtungsmatrix: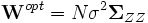 .
.
Der sich hieraus ergebende GIVE wird auch 2SLS-Schätzer genannt (two stage least squares), da er auch aus zwei aufeinander folgenden KQ-Regressionen gebildet werden kann.
Simulationsstudien haben gezeigt, dass die Varianzen der IV-Schätzer bei kleinen bis mittleren Stichproben häufig recht groß sind. Dies gilt insbesondere im Vergleich zu KQ-Schätzern und wird durch eine geringe Korrelation von endogenem Regressor und IV verschärft, da die Schätzer dann schon bei geringer Korrelation der IV mit dem Fehlerterm inkonsistent sind. Die Zahl der notwendigen Beobachtungen hängt vom jeweiligen Modellzusammenhang ab. Ein weiteres Problem stellt die Auswahl der Instrumente dar: Zwar können im einfachsten Fall beispielsweise exogene Variablen aus Vorperioden oder Differenzen aus diesen herangezogen werden, je weiter diese aber zeitlich entfernt sind, desto schwächer sind sie vermutlich. Auch rechentechnisch sind Grenzen gesetzt: So erreicht ein von Ahn/Schmidt vorgeschlagener IV-Schätzer mit zusätzlichen Momentenbedingungen für 15 Perioden und 10 erklärende Variablen 2.250 Spalten. Diese Größenordnungen sind von vielen Programmen selbst heute nicht lösbar. Die bezüglich der Momentenbedingungen getroffenen Annahmen können statistisch nicht getestet werden. Nur, wenn mehr Bedingungen als notwendig vorhanden sind (R>K), kann eine Aussage getroffen werden, ob Momentenbedingungen überflüssig sind, jedoch nicht welche. Sofern die Instrumente gültig sind, führen mehr Momentenbedingungen zu effizienteren Schätzern. Der Arellano-Bond-Schätzer (AB-Schätzer) erhöht die Zahl dieser Bedingungen durch die Berücksichtigung verzögerter Levels der abhängigen und prädeterminierten Variablen und Veränderungen der exogenen Variablen auf:
- m=(T-2)*(T-1)/2 Bedingungen bei einem Modell mit einer verzögerten Variablen und keinen exogenen Variablen: yit = γyi,t − 1 + εit,
- m=(T-2)*[K(T+1)+T]/2 Bedingungen bei einem Modell mit einer verzögerten Variablen und K strikt exogenen Variablen,
- m=(T-2)*[K(T+1)+(T-1)]/2 Bedingungen bei einem Modell mit einer verzögerten Variablen und K exogenen, prädeterminierten (vorherbestimmten) Variablen. Diese sind – im Gegensatz zu strikt exogenen Variablen – abhängig von vorherigen Realisationen des Fehlerterms:
![E[x_{it}\epsilon_{js}]\ne 0](/pictures/dewiki/57/96f13266e28d43cee455739934783e0c.png) für s<t und Null sonst.
für s<t und Null sonst.
Allgemein ergibt sich daraus der folgende Schätzer:
![\bold\hat\beta=[(\Delta \bold X)'\bold Z \bold A_N \bold Z'(\Delta \bold X)]^{-1} (\Delta \bold X)'\bold Z \bold A_N \bold Z'(\Delta \bold y)](/pictures/dewiki/52/40c380e0a2d595a1652453fe45e7555b.png) ,
,
mit der
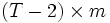 -Matrix
-Matrix 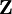 der Momentenbedingungen, der Gewichtungsmatrix
der Momentenbedingungen, der Gewichtungsmatrix 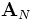 sowie den Veränderungen der erklärten bzw. erklärenden Variablen, (
sowie den Veränderungen der erklärten bzw. erklärenden Variablen, (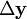 ) und (
) und (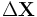 ). Das Verfahren setzt jedoch unkorrelierte Fehlerterme voraus. Bei abschließenden Tests muss beachtet werden, dass die Standardfehler nach unten hin verzerrt sind, was zu einer ungerechtfertigten Vernachlässigung einer erklärenden Variablen führen kann.
). Das Verfahren setzt jedoch unkorrelierte Fehlerterme voraus. Bei abschließenden Tests muss beachtet werden, dass die Standardfehler nach unten hin verzerrt sind, was zu einer ungerechtfertigten Vernachlässigung einer erklärenden Variablen führen kann.Dieses Verfahren ist mit kleineren Anpassungen auch für unbalancierte Paneldaten verwendbar.
Literatur
- Duncan, T.E., Duncan, S.C., Strycker, L.A., (et al) (1999): An introduction to latent variable growth curve modeling: Concepts, issues, and applications. Mahwah: Lawrence Erlbaum ISBN 0-805-85547-5
- Engel, U., Reinecke, J. (1994): Panelanalyse: Grundlagen, Techniken, Beispiele. Berlin: DeGruyter ISBN 3-110-13570-1
- Frees, Edward W. (2004): Longitudinal and Panel Data - analysis and applications in the social sciences, Cambridge et al.: Cambridge University Press, 2004
- Greene, William H. (2003): Econometric Analysis, 5. Aufl., Upper Saddle River, NJ: Prentice Hall, 2003
- Gujarati, Damodar N. (2003): Basic Econometrics, 4. Aufl., New York et al.: McGraw-Hill, 2002
- Muthén, B.O. (2004): Latent Variable Analysis: Growth mixture modeling an related techniques for longitudinal data. In Kaplan (Ed.), The Sage handbook of quantitative methodology for the social sciences (S.345-368). Thousand Oaks: Sage ISBN 0-761-92359-4
- Reinecke, J.: Strukturgleichungsmodelle in den Sozialwissenschaften. München[u.a.]: Oldenbourg, 2005 ISBN 3-486-57761-1
- Verbeek, Marno (2004): A Guide to Modern Econometrics, 2. Aufl., Chichester: John Wiley & Sons, 2004
- Wooldridge, Jeffrey M. (2002): Econometric analysis of cross section and panel data, Cambridge: MIT Press, 2002
Wikimedia Foundation.