Reguläre Ausdrücke

In der Informatik ist ein Regulärer Ausdruck (engl. regular expression, Abk. RegExp oder Regex) eine Zeichenkette, die der Beschreibung von Mengen beziehungsweise Untermengen von Zeichenketten mit Hilfe bestimmter syntaktischer Regeln dient. Reguläre Ausdrücke finden vor allem in der Softwareentwicklung Verwendung; für fast alle Programmiersprachen existieren Implementierungen.

Reguläre Ausdrücke stellen erstens eine Art Filterkriterium für Texte dar, indem der jeweilige reguläre Ausdruck in Form eines Musters mit dem Text abgeglichen wird. So ist es beispielsweise möglich, alle Wörter, die mit S beginnen und mit D enden, zu matchen (von englisch „to match“ – „auf etwas passen“, „übereinstimmen“, „eine Übereinstimmung finden“), ohne die zwischenliegenden Buchstaben explizit vorgeben zu müssen.

Ein weiteres Beispiel für den Einsatz als Filter ist die Möglichkeit, komplizierte Textersetzungen durchzuführen, indem man die zu suchenden Zeichenketten durch reguläre Ausdrücke beschreibt.

Zweitens lassen sich aus regulären Ausdrücken, als eine Art Schablone, auch Mengen von Wörtern erzeugen, ohne jedes Wort einzeln angeben zu müssen. So lässt sich beispielsweise ein Ausdruck angeben, der alle denkbaren Zeichenkombinationen (Wörter) erzeugt, die mit S beginnen und mit D enden.

Reguläre Ausdrücke in der theoretischen Informatik

Theoretische Grundlagen

Hinweis: In diesem Abschnitt wird die Kenntnis einiger Konzepte der Theorie der formalen Sprachen vorausgesetzt.

Reguläre Ausdrücke beschreiben eine Familie von formalen Sprachen und gehören damit zur Theoretischen Informatik. Hier bilden sie die unterste und somit ausdrucksschwächste Stufe der Chomsky-Hierarchie (Typ-3). Es lässt sich zeigen, dass zu jedem regulären Ausdruck ein gleichwertiger endlicher Automat existiert und umgekehrt. Dieser Automat ist einfach bestimmbar. Hieraus folgt die relativ einfache Implementierbarkeit regulärer Ausdrücke.

Der Mathematiker Stephen Kleene benutzte eine Notation, die er reguläre Mengen nannte. Die Mächtigkeit regulärer Ausdrücke reicht aus, um – von wenigen Ausnahmen abgesehen – die Morphologie einer natürlichen Sprache zu beschreiben.

Reguläre Ausdrücke unterstützen genau drei Operationen: Alternative, Verkettung und Wiederholung. Die formelle Definition sieht folgendermaßen aus:

Syntax

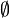1. $\emptyset$ (die leere Menge) ist ein regulärer Ausdruck.
2. $\varepsilon$ (das leere Wort) ist ein regulärer Ausdruck.
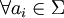3. $\forall a_i \in \Sigma$ ist a_i (jedes Zeichen aus dem zugrundeliegenden Alphabet) ein regulärer Ausdruck.
4. Sind x und y reguläre Ausdrücke, so sind auch (x | y) (Alternative), (xy) (Verkettung) und x ^* (Kleenesche Hülle) reguläre Ausdrücke.
5. Es gibt keine weiteren regulären Ausdrücke.

Anwendung regulärer Ausdrücke

Ken Thompson nutzte diese Notation in den 1960ern, um qed (eine Vorgängerversion des Unix-Editors ed) zu bauen und später das Werkzeug grep zu schreiben. Seither implementieren sehr viele Programme und Bibliotheken von Programmiersprachen Funktionen, um reguläre Ausdrücke zum Suchen und Ersetzen von Zeichenketten zu nutzen. Beispiele dafür sind die Programme sed, grep, emacs und Bibliotheken der Programmiersprachen Perl, C, Java, Python, Ruby und das .NET Framework. Auch die Textverarbeitung und die Tabellenkalkulation des Office-Paketes OpenOffice.org bieten die Möglichkeit, mit regulären Ausdrücken im Text zu suchen.

Die jeweiligen Regexp-Implementierungen sind jedoch nicht alle gleich. In den Programmiersprachen haben sich überwiegend die PCRE (Perl Compatible Regular Expressions) durchgesetzt, die sich an der Umsetzung in Perl orientieren. Daneben wird – vor allem in der Linux-Welt – z. B. zwischen BRE (basic regular expressions) und ERE (extended regular expressions) unterschieden.
Einige Programme wie z. B. der Texteditor vim bieten die Möglichkeit, zwischen verschiedenen Regexp-Umsetzungen hin- und herzuschalten.

Die meisten heutigen Implementierungen unterstützen Erweiterungen wie z. B. Rückwärtsreferenzen (backreferences). Hierbei handelt es sich nicht mehr um reguläre Ausdrücke im Sinne der theoretischen Informatik, denn die so erweiterten Ausdrücke gehören nicht mehr notwendigerweise zum Typ 3 der Chomsky-Hierarchie.

Häufig werden reguläre Ausdrücke angewendet, um Programm-Quelltexte lexikalisch zu analysieren, beispielsweise in Compilern oder zur Syntaxhervorhebung in Editoren. Dazu wird der Quelltext mit einem (dann vergleichsweise komplexen) regulären Ausdruck in sogenannte Tokens (Schlüsselwörter, Operatoren usw.) zerlegt. Werden Teile des Quelltextes nicht vom regulären Ausdruck erkannt, so hat sich ein Syntaxfehler in den Quelltext eingeschlichen. Die syntaktische oder semantische Analyse eines Programms kann jedoch normalerweise nicht mit regulären Ausdrücken durchgeführt werden, dafür wird eine kontextfreie Sprache benötigt.

Elemente, mit denen sich ein regulärer Ausdruck festlegen lässt

Die folgenden Syntaxbeschreibungen beziehen sich auf die Syntax der gängigen Implementierungen mit Erweiterungen, sie entsprechen also nur teilweise der obigen Definition aus der theoretischen Informatik.

Eine häufige Anwendung regulärer Ausdrücke besteht darin, spezielle Zeichenketten in einer Menge von Zeichenketten zu finden. Die im Folgenden angegebene Beschreibung ist eine (oft benutzte) Konvention, um Konzepte wie Zeichenklasse, Quantifizierung, Verknüpfung und Zusammenfassen konkret zu realisieren. Hierbei wird ein regulärer Ausdruck aus den Zeichen des zugrunde liegenden Alphabets in Kombination mit den Metazeichen [ ] ( ) { } |  ? + - * ^ $ \ . (teilweise kontextabhängig) gebildet. Die Meta-Eigenschaft eines Zeichens kann durch ein vorangestelltes Backslash-Zeichen aufgehoben werden. Alle übrigen Zeichen des Alphabets stehen für sich selbst.

Zeichenliterale

Diejenigen Zeichen, die direkt (wörtlich, literal) übereinstimmen müssen, werden auch direkt notiert. Je nach System gibt es auch Möglichkeiten, das Zeichen durch den Oktal- oder Hexadezimalcode (\ooo bzw. \xhh) oder die hexadezimale Unicode-Position (\uhhhh) anzugeben.

Beliebiges Zeichen

Ein Punkt (.) bedeutet, dass an seinem Platz ein (fast) beliebiges Zeichen stehen kann. Abhängig vom verwendeten Programm oder dessen Einstellungen kann ein Punkt auch für Newline (Zeilenumbruch) stehen. Die meisten Implementierungen sehen standardmäßig Newline nicht als beliebiges Zeichen an, jedoch kann in einigen Programmen mithilfe des sogenannten s-Modifiers (z. B. in /foo.bar/s) ebendies erreicht werden.

Ein Zeichen aus einer Auswahl

Mit eckigen Klammern lässt sich eine Zeichenauswahl definieren ([ und ]). Der Ausdruck in eckigen Klammern steht dann für genau ein Zeichen aus dieser Auswahl. Innerhalb dieser Zeichenklassendefinitionen haben einige Symbole andere Bedeutungen als im normalen Kontext. Teilweise ist die Bedeutung eines Symbols sogar vom Kontext abhängig, in dem es innerhalb der Klammern auftritt.

So bedeutet z. B. ein Zirkumflex „^“ am Anfang einer Zeichenklassendefinition, dass die Zeichenklasse negiert/invertiert wird (Komplement). Steht ein Zirkumflex jedoch irgendwo sonst in der Definition, ist es literal zu verstehen. Ebenfalls kontextabhängig ist das Bindestrich-Zeichen (-). Steht es zwischen zwei Zeichen der Klasse, z. B. „[a-g]“, so ist es als Beschreibung eines Zeichenintervalls oder Zeichenbereichs bzgl. der ASCII-Tabelle zu verstehen, d. h. das hier genannte Beispiel wäre äquivalent zu „[abcdefg]“. „[a-c-g]“ ist jedoch nicht zu „[abcdefg]“ äquivalent, sondern zu „[abc\-g]“, da „a-c“ bereits ein Zeichenintervall beschreiben und so von „-g“ unabhängig ist. Auch am Anfang oder Ende einer Zeichenklasse stehende Bindestriche werden literal interpretiert.

Beispiele für Zeichenauswahl

[egh]	eines der Zeichen „e“, „g“ oder „h“
[0-6]	eine Ziffer von „0“ bis „6“ (Bindestriche sind Indikator für einen Bereich)
[A-Za-z0-9]	ein beliebiger lateinischer Buchstabe oder eine beliebige Ziffer
[^a]	ein beliebiges Zeichen außer „a“ („^“ am Anfang einer Zeichenklasse negiert selbige)
[-A-Z], [A-Z-] bzw. [A-Z\-a-z]	Auswahl enthält auch das Zeichen „-“, wenn es das erste oder das letzte Zeichen einer Zeichenklasse ist bzw. wenn seine Metafunktion innerhalb einer Auswahl durch ein vorangestelltes „\“-Zeichen aufgehoben wird

In vielen neueren Implementationen können innerhalb der eckigen Klammern nach POSIX auch Klassen angegeben werden, die selbst wiederum eckige Klammern enthalten. Sie lauten beispielsweise:

Beispiele für Zeichenklassen

[:alnum:]	Alphanumerische Zeichen: [:alpha:] oder [:digit:].
[:alpha:]	Buchstaben: [:lower:] oder [:upper:].
[:blank:]	Leerzeichen oder Tabulator.
[:cntrl:]	Steuerzeichen. Im ASCII sind das die Zeichen 00 bis 1F, und 7F (DEL).
[:digit:]	die Ziffern 0 bis 9.
[:graph:]	Graphische Zeichen: [:alnum:] oder [:punct:].
[:lower:]	Kleinbuchstaben1: nicht notwendigerweise nur von a bis z.
[:print:]	Druckbare Zeichen: [:alnum:], [:punct:] und Leerzeichen.
[:punct:]	Zeichen wie: ! " # $ % & ' ( ) * + , - . / : ; < = > ? @ [ \ ] ^ _ ` { | } ~ .
[:space:]	Whitespace: Horizontaler und vertikaler Tabulator, Zeilen- und Seitenvorschub, Wagenrücklauf und Leerzeichen.
[:upper:]	Großbuchstaben1: nicht notwendigerweise nur von A bis Z.
[:xdigit:]	Hexadezimale Ziffern: 0 bis 9, A bis F, a bis f.

¹Was Buchstaben sind, ist im Allgemeinen locale-abhängig, also abhängig von der eingestellten Region und Sprache.^[1]

Vordefinierte Zeichenklassen

Es gibt vordefinierte Zeichenklassen, die allerdings nicht von allen Implementierungen unterstützt werden, da sie lediglich Kurzformen sind und auch durch eine Zeichenauswahl beschrieben werden können. Wichtige Zeichenklassen sind:

\d	eine Ziffer [0-9]
\D	ein Zeichen, das keine Ziffer ist, also [^\d]
\w	ein Buchstabe, eine Ziffer oder der Unterstrich, also [a-zA-Z_0-9] (und evtl. weitere Buchstaben, z. B. Umlaute)
\W	ein Zeichen, das weder Buchstabe noch Zahl noch Unterstrich ist, also [^\w]
\s	Whitespace; meistens die Klasse der Steuerzeichen \f, \n, \r, \t und \v
\S	ein Zeichen, das kein Whitespace ist [^\s]

Quantoren

Quantoren (engl. quantifier, auch Quantifizierer oder Wiederholungsfaktoren) erlauben es, den vorherigen Ausdruck in verschiedener Vielfachheit in der Zeichenkette zuzulassen.

?	Der voranstehende Ausdruck ist optional, er kann einmal vorkommen, muss es aber nicht, d. h. der Ausdruck kommt null- oder einmal vor. (Dies entspricht {0,1})
+	Der voranstehende Ausdruck muss mindestens einmal vorkommen, darf aber auch mehrfach vorkommen. (Dies entspricht {1,})
*	Der voranstehende Ausdruck darf beliebig oft (auch keinmal) vorkommen. (Dies entspricht {0,})
{n}	Der voranstehende Ausdruck muss exakt n-mal vorkommen.
{min,}	Der voranstehende Ausdruck muss mindestens min-mal vorkommen.
{,max}	Der voranstehende Ausdruck darf maximal max-mal vorkommen.
{min,max}	Der voranstehende Ausdruck muss mindestens min-mal und darf maximal max-mal vorkommen.

Die Quantoren beziehen sich dabei auf den vorhergehenden regulären Ausdruck, jedoch nicht zwangsläufig auf die durch ihn gefundene Übereinstimmung. So wird zwar zum Beispiel durch a+ ein „a“ oder auch „aaaa“ vertreten, jedoch entspricht [0-9]+ nicht nur sich wiederholenden gleichen Ziffern, sondern auch Folgen gemischter Ziffern, beispielsweise „072345“.

Weitere Beispiele sind:

• „[ab]+“ entspricht „a“, „b“, „aa“, „bbaab“ etc.
• „[0-9]{2,5}“ entspricht zwei, drei, vier oder fünf Ziffern in Folge, z. B. „42“, „54072“, jedoch nicht zum Beispiel die Zeichenfolgen „0“, „1.1“ oder „a1a1“.

Soll eine Zeichenkette nur aus dem gesuchten Muster bestehen (und es nicht nur enthalten), so muss in den meisten Implementierungen explizit definiert werden, dass das Muster von Anfang (\A oder ^)¹ bis zum Ende der Zeichenkette (\Z, \z oder $)¹ reichen soll, ansonsten matcht zum Beispiel [0-9]{2,5} auch bei der Zeichenkette „1234507“ die Teilzeichenkette „12345“. Aus dem gleichen Grund würde bspw. a* immer matchen, da jeder String, selbst der leere „“, mind. 0-mal das Zeichen „a“ enthält.

¹Die Zeichen ^ und $ matchen im multiline-Modus (d. i. wenn der m-Modifier gesetzt wird) auch Zeilenanfänge und -enden.

Quantoren sind von Natur aus „gierig“ (engl. greedy). Das heißt ein regulärer Ausdruck wird zur größtmöglichen Übereinstimmung aufgelöst. Da dieses Verhalten jedoch nicht immer so gewollt ist, lassen sich bei vielen neueren Implementierungen Quantoren als „genügsam“ oder „zurückhaltend“ (engl. non-greedy, reluctant) deklarieren. Z. B. in Perl wird hierfür dem Quantor ein Fragezeichen ? nachgestellt. Die Implementierung von genügsamen Quantoren ist vergleichsweise aufwändig (erfordert Backtracking), weshalb nicht alle Implementierungen diese unterstützen.

Beispiel (Perl-Syntax)

Angenommen es wird auf den String „ABCDEB“ der reguläre Ausdruck A.*B angewendet, so würde er den kompletten String „ABCDEB“ finden. Mit Hilfe des „non-greedy“-Quantors „*?“ matcht der neue Ausdruck, also A.*?B, nur die Zeichenkette „AB“, bricht also die Suche nach dem ersten gefundenen „B“ ab. Ein äquivalenter regulärer Ausdruck für Interpreter, die diesen Quantor nicht unterstützen, wäre A[^B]*B.

Possessives Verhalten

Eine Variante des oben beschriebenen gierigen Verhaltens ist das possessive Matching. Da hierbei jedoch das Backtracking verhindert wird, werden einmal übereinstimmende Zeichen nicht wieder freigegeben. Aufgrund dessen finden sich in der Literatur auch die synonymen Bezeichnungen atomic grouping, independant subexpression oder non-backtracking subpattern. Die Syntax für diese Konstrukte variiert bei den verschiedenen Programmiersprachen. Ursprünglich wurden solche Subpattern in Perl durch (?>Ausdruck) formuliert. Daneben existieren seit Perl 5.10 die äquivalenten, in Java bereits üblichen possessiven Quantoren ++, *+, ?+ und {min,max}+.

Beispiel

Angenommen es wird auf den String „ABCDEB“ der reguläre Ausdruck A.*+B angewendet, so würde der Matching-Versuch fehlschlagen. Bei der Abarbeitung des regulären Ausdrucks würde der Teil .*+ bis zum Ende der Zeichenkette eine Übereinstimmung finden. Um erfolgreich zu matchen, müsste ein Zeichen, hier also das „B“, wieder freigegeben werden. Der possessive Quantor verbietet dies aufgrund des unterdrückten Backtrackings, weshalb keine erfolgreiche Übereinstimmung gefunden werden kann.

Gruppierungen und Rückwärtsreferenzen

Ausdrücke lassen sich mit runden Klammern ( und ) zusammenfassen: Etwa erlaubt „(abc)+“ ein „abc“ oder ein „abcabc“ etc.

Einige Implementierungen speichern die gefundenen Übereinstimmungen von Gruppierungen ab und ermöglichen deren Wiederverwendung im Regulären Ausdruck oder bei der Textersetzung. Diese werden Rückwärtsreferenzen (engl. back references) genannt. Häufig wird dazu die Schreibweise \n oder $n verwendet, wobei n die Übereinstimmung der n-ten Gruppierung entspricht. Eine Sonderstellung stellt dabei n=0 dar, das meist für die Übereinstimmung des gesamten regulären Ausdruck steht.

Beispiel

Ein Suchen und Ersetzen mit AA(.*?)BB als regulären Suchausdruck und \1 als Ersetzung ersetzt alle Zeichenketten, die von AA und BB eingeschlossen sind, durch den zwischen AA und BB enthaltenen Text. D. h. AA und BB und der Text dazwischen werden ersetzt durch den Text, der ursprünglich zwischen AA und BB stand, also fehlen AA und BB im Ergebnis.

Interpreter von regulären Ausdrücken, die Rückwärtsreferenzen zulassen, entsprechen nicht mehr dem Typ 3 der Chomsky-Hierarchie. Mit dem Pumping-Lemma lässt sich einfach zeigen, dass ein regulärer Ausdruck, der feststellt, ob in einer Zeichenkette vor und nach der 1 die gleiche Anzahl von 0 steht, keine reguläre Sprache ist.

Daneben gibt es auch noch Gruppierungen, die keine Rückwärtsreferenz erzeugen (engl. non-capturing). Die Syntax dafür lautet in den meisten Implementierungen (?:…). Regexp-Dokumentationen weisen darauf hin, dass die Erzeugung von Rückwärtsreferenzen stets vermieden werden soll, wenn kein späterer Zugriff auf sie erfolge. Denn die Erzeugung der Referenzen kostet Ausführungszeit und belegt Platz zur Speicherung der gefundenen Übereinstimmung. Zudem lassen die Implementationen nur eine begrenzte Anzahl an Rückwärtsreferenzen zu (häufig nur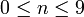 $0\le n\le9$).

Beispiel

Mit dem regulären Ausdruck „\d+(?:-\d+)*“ können Folgen von durch Bindestriche getrennte Zahlenfolgen gefunden werden, ohne dabei die letzte durch einen Bindestrich getrennte Zahlenfolge als Rückreferenz zu erhalten.

Alternativen

Man kann alternative Ausdrücke mit dem „|“-Symbol zulassen.

Beispiel

„ABC|abc“ bedeutet „ABC“ oder „abc“, aber z. B. nicht „Abc“.

Weitere Zeichen

Um die oft auf Zeichenketten bezogenen Anwendungen auf dem Computer zu unterstützen, werden in der Regel zusätzlich zu den bereits genannten die folgenden Zeichen definiert:

^	steht für den Zeilenanfang (nicht zu verwechseln mit „^“ bei der Zeichenauswahl mittels „[“ und „]“).
$	kann je nach Kontext für das Zeilen- oder Stringende stehen, wobei bei manchen Implementierungen noch ein „\n“ folgen darf. Das tatsächliche Ende wird von \z gematcht.
\	hebt gegebenenfalls die Metabedeutung des nächsten Zeichens auf. Beispielsweise lässt der Ausdruck „(A\*)+“ die Zeichenketten „A*“, „A*A*“, usw. zu. Auf diese Weise lässt sich auch ein Punkt „.“ mit „\.“ suchen, während nach „\“ mit „\\“ gesucht wird.
\b	leere Zeichenkette am Wortanfang oder am Wortende
\B	leere Zeichenkette, die nicht den Anfang oder das Ende eines Wortes bildet
\<	leere Zeichenkette am Wortanfang
\>	leere Zeichenkette am Wortende
\n	ein Zeilenumbruch im Unix-Format
\r	ein Zeilenumbruch im Mac-Format
\r\n	ein Zeilenumbruch im Windows-Format

Look-around assertions

Perl Version 5 führte zusätzlich zu den üblichen regulären Ausdrücken auch look-ahead und look-behind assertions (etwa "vorausschauende" bzw. "nach hinten schauende" Annahme/Behauptung) ein, was unter dem Begriff look-around assertions zusammengefasst wird.^[2] Diese Konstrukte erweitern die regulären Ausdrücke um die Möglichkeit, kontextsensitive Bedingungen zu formulieren, ohne den Kontext selbst zu matchen. D. h., möchte man alle Zeichenfolgen "Sport", denen die Zeichenfolge "verein" folgt, matchen, ohne die Zeichenfolge "verein" selbst zu matchen, wäre dies mit einer look-ahead assertion möglich: Sport(?=verein). Aufgrund der Eigenschaft, dass der angegebene Kontext (im Beispiel "verein") zwar angegeben wird, jedoch kein expliziter Bestandteil des gematchten Strings (hier "Sport") ist, wird im Zusammenhang mit den assertions meist das Attribut zero-width mitgenannt. Die vollständigen Bezeichnungen lauten somit, je nachdem ob ein bestimmter Kontext gefordert (positiv) oder verboten (negativ) ist, zero-width positive/negative look-ahead/behind assertions. Die Bezeichnungen der Richtungen rühren daher, dass Regexp-Parser einen String immer von links nach rechts abarbeiten.

Definition	Bezeichnung	Erklärung	Schreibweise
(?=Ausdruck)	positive look-ahead assertion	Ausdruck muss auf vorgenannten Ausdruck folgen	Ausdruck(?=Ausdruck)
(?!Ausdruck)	negative look-ahead assertion	Ausdruck darf nicht auf vorgenannten Ausdruck folgen	Ausdruck(?!Ausdruck)
(?<=Ausdruck)	positive look-behind assertion	Ausdruck muss nachfolgendem Ausdruck vorausgehen	(?<=Ausdruck)Ausdruck
(?<!Ausdruck)	negative look-behind assertion	Ausdruck darf nachfolgendem Ausdruck nicht vorausgehen	(?<!Ausdruck)Ausdruck

Look-arounds werden neben Perl und PCRE unter anderem von .NET Framework sowie von Python unterstützt. Auch einige Texteditoren wie z. B. Vim bieten die Möglichkeit, wenn auch mit teilweise anderer Syntax.

Bedingte Ausdrücke

Relativ wenig verbreitet sind bedingte Ausdrücke. Diese sind u. a. in Perl, PCRE und dem .NET Framework einsetzbar. Python bietet für solche Ausdrücke in Zusammenhang mit look-around assertions nur eingeschränkte Funktionalität.^[3]

(?(?=Bedingung)wahr-Ausdruck|falsch-Ausdruck)

Wenn der gegebene Ausdruck „Bedingung“ gefunden wird, kommt der „wahr-Ausdruck“ zur Anwendung. Wenn der Suchausdruck nicht gefunden werden kann, kommt der „falsch-Ausdruck“ zur Anwendung.

Literatur

Reguläre Ausdrücke

• Jeffrey Friedl: Reguläre Ausdrücke. O’Reilly, ISBN 3-89721-720-1.
• Tony Stubblebine: Reguläre Ausdrücke – kurz und gut. O’Reilly, ISBN 3-89721-264-1.
• Mehran Habibi: Real World Regular Expressions with Java 1.4. Springer, ISBN 1-59059-107-0.

Reguläre Ausdrücke und natürliche Sprachen

• Kenneth R. Beesley, Lauri Karttunen: Finite-State Morphology. Distributed for the Center for the Study of Language and Information. 2003, 696 p. (est.). 2003 Series: (CSLI-SCL) Studies in Computational Linguistics

Reguläre Ausdrücke und Automatentheorie

• Jan Lunze: Ereignisdiskrete Systeme, Seiten 160-192, Oldenbourg, 2006, ISBN 3-486-58071-X

Siehe auch

• Wildcard
• PCRE (Perl-kompatible reguläre Ausdrücke)
• ω-regulärer Ausdruck

Weblinks

• Online reguläre Ausdrücke auswerten
• Online reguläre Ausdrücke auswerten (englisch)
• Reguläre Sprachen, reguläre Ausdrücke
• Regex-Kurs für Anfänger mit Übungen
• POSIX-Spezifikation für reguläre Ausdrücke (englisch)
• Perl–Syntax regulärer Ausdrücke (englisch)
• Sehr umfangreiches Tutorial zu regulären Ausdrücken und den verschiedenen Implementierungen (englisch)

Referenzen

1. ↑ The Open Group Base Specifications, RE Bracket Expression, IEEE Std 1003.1, 2004
2. ↑ Regular-Expressions.info: Lookahead and Lookbehind Zero-Width Assertions
3. ↑ Regular-Expressions.info: If-Then-Else Conditionals in Regular Expressions