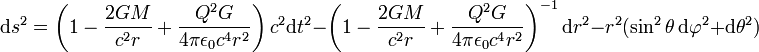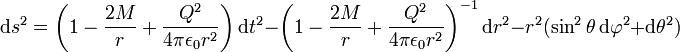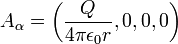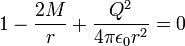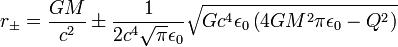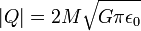Reissner-Nordstrom-Metrik
- Reissner-Nordstrom-Metrik
-
Die Reissner-Nordström-Metrik (nach Hans Reissner und Gunnar Nordström) ist eine exakte, asymptotisch flache, stationäre und sphärisch-symmetrische Lösung der Einstein-Gleichungen für elektrisch geladene, nicht-rotierende Schwarze Löcher.
Linienelement
Das Linienelement der Reissner-Nordström-Metrik hat die Form:
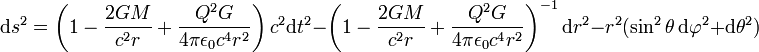
wobei M die Masse und Q die elektrische Ladung des Objektes sind. In den sogenannten natürlichen Einheiten wird c = G = 1 gesetzt, sodass die Metrik auch in der Form
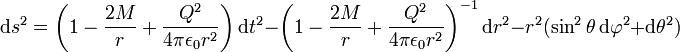
geschrieben werden kann. Der Einfachheit halber wird eine elektrische Punktladung im Koordinatenursprung angenommen. Magnetische Felder und Kreisströme werden vernachlässigt. Das elektromagnetische Viererpotential ist somit ein Coulomb-Potential:
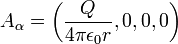
Horizonte und Singularitäten
Wie bei der Schwarzschild-Metrik liegt der Ereignishorizont bei demjenigen Radius, wo die Metrik singulär wird. Das bedeutet
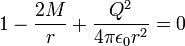
Aufgrund der quadratischen Abhängigkeit vom Radius r finden sich jedoch zwei Lösungen dieser Gleichung. Daher gibt es einen Ereignishorizont bei r + und einen zusätzlichen Cauchy-Horizont bei r − , der weiter innen liegt.
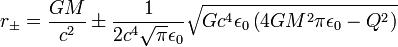
Für den Fall
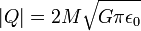
verschwindet die Wurzel in 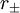 und die beiden Horizonte fallen zu einem einzelnen zusammen. Ist hingegen
und die beiden Horizonte fallen zu einem einzelnen zusammen. Ist hingegen
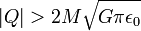 ,
,
so ist die Wurzel imaginär, womit es keinen Horizont gibt. Man spricht in diesem Fall von einer nackten Singularität, die nach heutiger Auffassung allerdings nicht existieren kann ("Cosmic Censorship" Hypothese). Moderne supersymmetrische Theorien verbieten sie in der Regel.
Für Q = 0 geht die Reissner-Nordström-Metrik in die Schwarzschild-Metrik über. ihre Singularitäten liegen dann bei r = 0 und r = 2M ergeben.
In der Astrophysik spielen elektrisch geladene Schwarze Löcher (also auch die Kerr-Newman-Metrik) eine untergeordnete Rolle, weil man annimmt, dass jede Ladung des Loches recht schnell durch elektrische Ströme, nämlich die Akkretionsflüsse, neutralisiert wird.
Quellen
Weblinks
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Reissner-Nordstrøm-Metrik — Die Reissner Nordström Metrik (nach Hans Reissner und Gunnar Nordström) ist eine exakte, asymptotisch flache, stationäre und sphärisch symmetrische Lösung der Einstein Gleichungen für elektrisch geladene, nicht rotierende Schwarze Löcher.… … Deutsch Wikipedia
Reissner-Nordström-Metrik — Die Reissner Nordström Metrik (nach Hans Reissner und Gunnar Nordström) ist eine exakte, asymptotisch flache, stationäre und sphärisch symmetrische Lösung der Einstein Gleichungen für elektrisch geladene, nicht rotierende Schwarze Löcher.… … Deutsch Wikipedia
Reissner-Nordström-Lösung — Die Reissner Nordström Metrik (nach Hans Reissner und Gunnar Nordström) ist eine exakte, asymptotisch flache, stationäre und sphärisch symmetrische Lösung der Einstein Gleichungen für elektrisch geladene, nicht rotierende Schwarze Löcher.… … Deutsch Wikipedia
Reissner — ist der Familienname folgender Personen: Eric Reissner (1913–1996), deutsch amerikanischer Mathematiker und Ingenieur, Sohn von Hans Jacob Reissner Hans Jacob Reissner (1874–1967), deutscher Ingenieur, Mathematiker und Physiker Larissa Reissner… … Deutsch Wikipedia
Hans Reissner — Hans Jacob Reissner. Hans Jacob Reissner (* 18. Januar 1874 in Berlin; † 2. Oktober 1967 in Colton (Oregon), USA) war ein deutscher Ingenieur, Mathematiker und Physiker. Reissner erlangte nach seiner Schulausbildung in Berlin 1897 den Titel eines … Deutsch Wikipedia
Gunnar Nordström — Gunnar Nordström. Gunnar Nordström (* 12. März 1881 in Helsinki; † 24. Dezember 1923 ebenda) war ein finnischer theoretischer Physiker, der bekannt ist für seine Theorie der Gravitation, die ein früher Konkurrent der Allgemeinen… … Deutsch Wikipedia
Hans Jacob Reissner — Hans Jacob Reissner. Hans Jacob Reissner (* 18. Januar 1874 in Berlin; † 2. Oktober 1967 in Colton (Oregon), USA) war ein deutscher Ingenieur, Mathematiker und Physiker. Reissner erlangte nach seiner Schulausbildung in Berlin 1897 den Titel eines … Deutsch Wikipedia
Kerr-Metrik — Die Kerr Metrik [1] ist eine Vakuumlösung der einsteinschen Feldgleichungen für ungeladene, rotierende schwarze Löcher. Diese Lösung wird nach Roy Patrick Kerr benannt, der sie als erster berechnete. Das Linienelement lässt sich in Boyer… … Deutsch Wikipedia
Schwarzschild-Metrik — Die Schwarzschild Metrik (auch: Schwarzschild Lösung) bezeichnet, speziell im Rahmen der allgemeinen Relativitätstheorie, eine Lösung der einsteinschen Feldgleichungen, die das Gravitationsfeld einer homogenen, nicht geladenen und nicht… … Deutsch Wikipedia
Kerr-Newman-Metrik — Die Kerr Newman Metrik (nach Roy Patrick Kerr und Ezra T. Newman) ist eine exakte, asymptotisch flache, stationäre und axialsymmetrische Lösung der Einstein Gleichungen für elektrisch geladene, rotierende Schwarze Löcher. Das Linienelement hat… … Deutsch Wikipedia
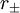 und die beiden Horizonte fallen zu einem einzelnen zusammen. Ist hingegen
und die beiden Horizonte fallen zu einem einzelnen zusammen. Ist hingegen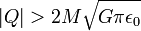 ,
,