Rekursiv aufzählbar

Die rekursive Aufzählbarkeit ist ein Begriff aus der Berechenbarkeitstheorie. Er gibt Aufschluss darüber, ob sich die Elemente einer vorgegebenen Menge schrittweise von einem Computer erzeugen lassen.

Definition

Eine Menge M heißt rekursiv aufzählbar, falls es eine surjektive, berechenbare Funktion 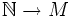$\mathbb{N} \to M$ gibt. Die leere Menge ist rekursiv aufzählbar.

Eine Menge von Zahlen M = S₁,S₂,..., ist dann aufzählbar, wenn es eine Funktion f(x) gibt, die alle Elemente von M berechnen kann (f(1) = S1, f(2) = S2,...).

Die Klasse der rekursiv aufzählbaren Mengen wird in der Literatur meist mit RE (vom englischen Recursively Enumerable) bezeichnet.

Äquivalenzen zur Definition

• M ist rekursiv aufzählbar.
• M ist semi-entscheidbar.
• M ist vom Typ 0.
• M ist die Menge aller Berechnungsergebnisse einer Turingmaschine.
• χ'_M, die halbe charakteristische Funktion, ist Turing-, WHILE- oder GOTO-berechenbar.
• M ist Definitionsbereich einer berechenbaren Funktion.
• M ist Wertebereich einer rekursiven Funktion.

Eigenschaften

• Jede endliche Menge ist rekursiv aufzählbar.
• Eine Menge ist genau dann rekursiv aufzählbar, wenn sie semi-entscheidbar ist.
• Jede rekursiv aufzählbare Menge ist abzählbar, aber nicht alle abzählbaren Mengen sind rekursiv aufzählbar.
• Jede unendliche rekursiv aufzählbare Sprache besitzt Teilmengen, die nicht rekursiv aufzählbar sind.
• Genau dann, wenn eine Menge und ihr Komplement rekursiv aufzählbar sind, dann ist sie bereits rekursiv entscheidbar.

Beispiele

• Die Menge der Paare der Form: (Programm, Eingabe) mit der Eigenschaft: das Programm hält mit der Eingabe ist rekursiv aufzählbar (siehe Halteproblem).
• Die Selbstanwendbarkeit ist rekursiv aufzählbar: In obigem Beispiel beschränken wir uns auf die Eingaben, die dem jeweiligen Programm entsprechen.
• Die Werte der Busy-Beaver-Funktion Σ(n) sind nicht rekursiv aufzählbar.