Rekursiv aufzählbare Menge
- Rekursiv aufzählbare Menge
-
Als semi-entscheidbare Menge (auch halb-entscheidbare Menge) wird in der Berechenbarkeitstheorie eine Menge A bezüglich einer Grundmenge M bezeichnet, wenn ihre partielle charakteristische Funktion 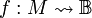 definiert durch
definiert durch

berechenbar ist. Die Menge M muss dazu gödelisierbar sein. In der Theorie setzt man zum einfacheren Vergleich direkt 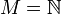 oder M = {0,1} * voraus. Im letzteren Fall hat man die Menge als das Wortproblem einer formalen Sprache dargestellt.
oder M = {0,1} * voraus. Im letzteren Fall hat man die Menge als das Wortproblem einer formalen Sprache dargestellt.
Hintergrund: Wenn eine Ausgabe 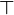 geliefert wird, ist eine positive Antwort eingetroffen; wenn diese Ausgabe nicht gekommen ist, muss man noch warten oder sie kommt nie. Es gibt semi-entscheidbare Mengen, deren Komplement nicht semi-entscheidbar ist.
geliefert wird, ist eine positive Antwort eingetroffen; wenn diese Ausgabe nicht gekommen ist, muss man noch warten oder sie kommt nie. Es gibt semi-entscheidbare Mengen, deren Komplement nicht semi-entscheidbar ist.
Berechenbare Mengen
In der Literatur taucht gelegentlich der Begriff der berechenbaren Menge auf. Dieser Begriff wird uneinheitlich verwendet. Es können damit entscheidbare Mengen oder semi-entscheidbare Mengen gemeint sein.
Eigenschaften
- Eine Menge ist genau dann semi-entscheidbar, wenn sie rekursiv aufzählbar ist.
- Eine Menge ist genau dann semi-entscheidbar, wenn sie der Wertebereich einer berechenbaren Funktion ist.
- Eine formale Sprache ist genau dann semi-entscheidbar, wenn sie Typ-0 ist.
- Eine Menge ist genau dann entscheidbar, wenn sie und ihr Komplement semi-entscheidbar sind.
Beispiele
- Das Halteproblem der Turingmaschinen ist semi-entscheidbar, denn man kann die gegebene Turingmaschine mit der gegebenen Eingabe laufen lassen und nach seiner Terminierung
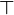 ausgeben. Das Komplement des Halteproblems ist nicht semi-entscheidbar.
ausgeben. Das Komplement des Halteproblems ist nicht semi-entscheidbar.
- Das Äquivalenzproblem der Turingmaschinen ist nicht semi-entscheidbar. Auch das Komplement des Äquivalenzproblems ist nicht semi-entscheidbar.
Siehe auch
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Aufzählbare Menge — Die rekursive Aufzählbarkeit ist ein Begriff aus der Berechenbarkeitstheorie. Er gibt Aufschluss darüber, ob sich die Elemente einer vorgegebenen Menge schrittweise von einem Computer erzeugen lassen. Inhaltsverzeichnis 1 Definition 2… … Deutsch Wikipedia
Rekursiv aufzählbare Sprache — In der theoretischen Informatik ist eine rekursiv aufzählbare Sprache oder semientscheidbare Sprache L dadurch definiert, dass es eine Turingmaschine gibt, die alle Wörter aus L akzeptiert, aber keine Wörter, die nicht in L liegen. Im Unterschied … Deutsch Wikipedia
Rekursiv aufzählbar — Die rekursive Aufzählbarkeit ist ein Begriff aus der Berechenbarkeitstheorie. Er gibt Aufschluss darüber, ob sich die Elemente einer vorgegebenen Menge schrittweise von einem Computer erzeugen lassen. Inhaltsverzeichnis 1 Definition 2… … Deutsch Wikipedia
Aufzählbar — Die rekursive Aufzählbarkeit ist ein Begriff aus der Berechenbarkeitstheorie. Er gibt Aufschluss darüber, ob sich die Elemente einer vorgegebenen Menge schrittweise von einem Computer erzeugen lassen. Inhaltsverzeichnis 1 Definition 2… … Deutsch Wikipedia
Aufzählbarkeit — Die rekursive Aufzählbarkeit ist ein Begriff aus der Berechenbarkeitstheorie. Er gibt Aufschluss darüber, ob sich die Elemente einer vorgegebenen Menge schrittweise von einem Computer erzeugen lassen. Inhaltsverzeichnis 1 Definition 2… … Deutsch Wikipedia
Rekursive Aufzählbarkeit — Die rekursive Aufzählbarkeit ist ein Begriff aus der Berechenbarkeitstheorie. Er gibt Aufschluss darüber, ob sich die Elemente einer vorgegebenen Menge schrittweise von einem Computer erzeugen lassen. Inhaltsverzeichnis 1 Definition 2… … Deutsch Wikipedia
Turingreduktion — Die Reduktion ist eine Methode der Theoretischen Informatik. Eine Reduktion ist die Lösung eines Problems mit Hilfe eines hypothetischen Algorithmus für ein anderes Problem. Die Reduzierbarkeit ist somit eine Relation zwischen zwei Problemen.… … Deutsch Wikipedia
Chomsky-Typ — Chomsky Hierarchie, gelegentlich Chomsky–Schützenberger Hierarchie, (benannt nach dem Linguisten Noam Chomsky und dem Mathematiker Marcel Schützenberger) ist ein Begriff aus der Theoretischen Informatik und bezeichnet eine Hierarchie von Klassen… … Deutsch Wikipedia
Chomsky Hierarchie — Chomsky Hierarchie, gelegentlich Chomsky–Schützenberger Hierarchie, (benannt nach dem Linguisten Noam Chomsky und dem Mathematiker Marcel Schützenberger) ist ein Begriff aus der Theoretischen Informatik und bezeichnet eine Hierarchie von Klassen… … Deutsch Wikipedia
Chomskyhierarchie — Chomsky Hierarchie, gelegentlich Chomsky–Schützenberger Hierarchie, (benannt nach dem Linguisten Noam Chomsky und dem Mathematiker Marcel Schützenberger) ist ein Begriff aus der Theoretischen Informatik und bezeichnet eine Hierarchie von Klassen… … Deutsch Wikipedia
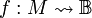 definiert durch
definiert durch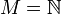 oder M = {0,1} * voraus. Im letzteren Fall hat man die Menge als das Wortproblem einer formalen Sprache dargestellt.
oder M = {0,1} * voraus. Im letzteren Fall hat man die Menge als das Wortproblem einer formalen Sprache dargestellt.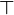 geliefert wird, ist eine positive Antwort eingetroffen; wenn diese Ausgabe nicht gekommen ist, muss man noch warten oder sie kommt nie. Es gibt semi-entscheidbare Mengen, deren Komplement nicht semi-entscheidbar ist.
geliefert wird, ist eine positive Antwort eingetroffen; wenn diese Ausgabe nicht gekommen ist, muss man noch warten oder sie kommt nie. Es gibt semi-entscheidbare Mengen, deren Komplement nicht semi-entscheidbar ist.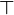 ausgeben. Das Komplement des Halteproblems ist nicht semi-entscheidbar.
ausgeben. Das Komplement des Halteproblems ist nicht semi-entscheidbar.
