- Autokovarianzfunktion
-
Die Autokovarianzfunktion untersucht im Gegensatz zur Kovarianz nicht den Zusammenhang zwischen zwei verschiedenen Zufallsvariablen, sondern zwischen Realisationen der gleichen Zufallsvariablen zu unterschiedlichen Zeitpunkten. Es handelt sich hierbei folglich um ein Maß des Zusammenhangs von Beobachtungsdaten. Formal lässt sich die Autokovarianzfunktion wie folgt notieren:
![\gamma(t_1,t_2)=E[({Y_t}_1-{\mu_t}_1)({Y_t}_2-{\mu_t}_2)]; \qquad \gamma(t_1,t_2)\in\mathbb{R}](/pictures/dewiki/49/10ed9adc50fd6cedf681c9919eef86ea.png)
- Hierbei bedeuten:
-
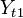
Realisation der Zufallsvariable Y zum Zeitpunkt t1 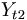
Realisation der Zufallsvariable Y zum Zeitpunkt t2 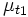
Erwartungswert der Zufallsvariable Y zum Zeitpunkt t1 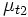
Erwartungswert der Zufallsvariable Y zum Zeitpunkt t2 E[...] Erwartungswert von [...] γ(t1,t2) Autokovarianz der Zufallsvariable Y bezogen auf die Zeitpunkte t1 und t2
Die lineare Abhängigkeit zwischen
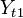 und
und 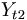 ist umso stärker, je größer der Betrag von γ(t1,t2).
ist umso stärker, je größer der Betrag von γ(t1,t2).
Die Autokovarianz eines stationären Prozesses ist nicht von der Lage der Zeitpunkte, sondern nur von der Zeitdifferenz abhängig.Siehe auch: Autokorrelation, Partielle Autokorrelationsfunktion
Wikimedia Foundation.
