Partielle Autokorrelationsfunktion

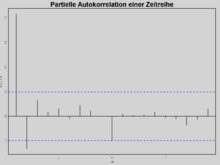Partielle Autokorrelation der Zeitreihe der Tiefen des Huronsee

Die partielle Autokorrelationsfunktion (PAKF, engl. PACF) ist wie die Autokovarianzfunktion und die Autokorrelationsfunktion ein Instrument, um Abhängigkeiten zwischen den Werten einer Zeitreihe zu unterschiedlichen Zeiten zu identifizieren. Die PAKF misst den linearen Zusammenhang zwischen Y_t und Y_{t + k} unter Ausschaltung des Einflusses der dazwischen liegenden Variablen.

Bei autokorrelierten stationären Prozessen enthalten die Beobachtungen Y_t bis Y_{T − 1} Informationen über den erwarteten Betrag und Vorzeichen der Größe Y_T (mit $t<T \in \mathbb N$). Die partielle Autokorrelation drückt dann die zusätzliche Information über die Ausprägung von Y_T aus, die man erhält, wenn man darüber hinaus Y_{t − 1}, den Zustand des Prozesses zur Zeit t − 1, kennt.

Die formale Definition lautet bei zentrierten stationären Zeitreihen

$\varphi_{kk} := \operatorname{Corr}(Y_t, Y_{t-k}|Y_{t-1}, \cdots, Y_{t-k + 1})\quad k = 0,\pm 1,\pm 2, \cdots$

Die Operation $\operatorname{Corr}(\cdot,\cdot | \cdot)$ bezeichnet dabei die bedingte Korrelation, gebildet mit der bedingten Erwartung

$\operatorname{Corr}(W,Z|\mathcal{F}_t) := \frac{E(WZ|\mathcal{F}_t)-E(W|\mathcal{F}_t)E(Z|\mathcal{F}_t)} {E(W^2|\mathcal{F}_t)E(Z^2|\mathcal{F}_t)}.$

Die Funktion ist in k symmetrisch und ihre Werte liegen im Intervall [ − 1,1]. Es gilt φ₀₀ = 1.

Zur Bestimmung der PAKF gibt es verschiedene Verfahren:

• Yule-Walker-Gleichungen (nach George Udny Yule),
• Durbin-Levinson-Algorithmus.

Letztere Methode geht rekursiv vor. Mit ihr kann auch eine empirische PAKF (geschätzte PAKF) berechnet werden. Eine Approximation der Standardabweichung der empirischen PAKF ist mit der Quenouille-Approximation möglich:

$\hat\sigma(\hat\varphi_{kk})\approx\frac{1}{\sqrt{T}}$.

Quellen

• Box, G. E. P., Jenkins, G. M., und Reinsel, G. C. (1994). Time Series Analysis, Forecasting and Control, 3rd ed. Prentice Hall, Englewood Clifs, NJ.
• Brockwell, Peter J. und Davis, Richard A. (1987). Time Series: Theory and Methods, Springer-Verlang.
• Rinne H. (2003). Taschenbuch der Statistik, Verlag Harri Deutsch.