Retrakt

In der Kategorientheorie versteht man unter einer Retraktion einen Morphismus f, der ein Rechtsinverses besitzt, das heißt, zu dem es einen Morphismus g gibt mit f o g = id.

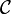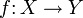Ein Objekt X einer Kategorie $\mathcal{C}$ heißt Retrakt eines Objekts $Y\in |\mathcal{C}|$, wenn es in $\mathcal{C}$ einen Pfeil $f\colon X\to Y$ und eine Retraktion 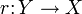$r\colon Y\to X$ zu f, also einen Pfeil r mit 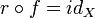$r\circ f=id_X$, gibt.

Topologische Räume

In der Topologie, also in der Kategorie Top, versteht man unter einer Retraktion eine stetige Funktion 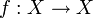$f: X \to X$, derart, dass f auf einer Teilmenge Y von X die Identität ist, also f alle Punkte von Y unverändert lässt, mit anderen Worten: f(y)=y für alle y aus Y.

Spezielle Kategorien

Topologische Räume

Ein Teilraum A eines topologischen Raums X heißt Retrakt von X, wenn es eine Retraktion r zur Einbettung 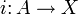$i\colon A\to X$ gibt.

A ist genau dann Retrakt von X, wenn jede stetige Abbildung 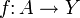$f\colon A\to Y$ stetig zu einer Abbildung 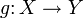$g\colon X\to Y$ fortgesetzt werden kann:

• Gibt es eine Retraktion 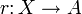$r\colon X\to A$, so ist 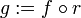$g := f \circ r$ stetige Fortsetzung.
• Eine Fortsetzung von id_A zu einer stetigen Abbildung 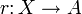$r\colon X\to A$ ist eine Retraktion.

Deformationsretrakt

A heißt Deformationsretrakt, wenn 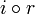$i\circ r$ homotop zu id_X relativ A ist.

Deformationsretraktionen sind spezielle Homotopieäquivalenzen, die diese Äquivalenzrelation erzeugen.

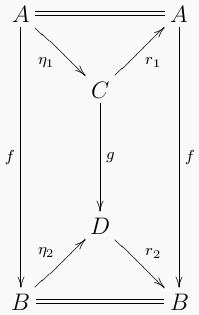
Pfeilkategorie

Ein Pfeil f ist Retrakt eines Pfeils g, wenn es eine natürliche Transformation 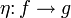$\eta\colon f\to g$ und eine Retraktion 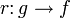$r\colon g\to f$ gibt, also das folgende Diagramm kommutiert: