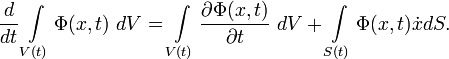Reynolds'scher Transportsatz

Der Reynolds'sche Transportsatz (nach Osborne Reynolds) stellt einen Zusammenhang zwischen der Euler'schen und der Lagrange'schen Betrachtungsweise eines Kontrollvolumens her. Er wird verwendet, um grundlegende Erhaltungssätze der Kontinuumsmechanik herzuleiten.

Darin ist Φ eine allgemeine Feldgröße, die sowohl vom Ort x als auch der Zeit t abhängt. Setzt man z. B. die Dichte ρ für Φ ein, dann erhält man eine Formulierung für die Massenerhaltung:

$\frac{d}{dt} \int\limits_{V(t)} \Phi(x,t)\ dV=\int\limits_{V(t)} \frac{\partial \Phi(x,t)}{\partial t}\ dV+\int\limits_{S(t)} \Phi(x,t) \dot{x} dS.$

S ist die das Volumen V umschließende Oberfläche (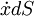$\dot{x} dS$ im letzten Term ist als Skalarprodukt von Geschwindigkeitsvektor und Normalenvektor der Oberfläche zu verstehen). Eine anschauliche Herleitung erhält man durch Transformation auf das zeitunabhängige Anfangsvolumen V₀ mit Einführung der zeitabhängigen Jacobi-Determinante | J(t) | .

Literatur

• Pieter Wesseling: Principles of Computational Fluid Dynamics, Springer Verlag, 2001