- Ritzsches Variationsverfahren
-
Das Rayleigh-Ritz-Prinzip (nach John William Strutt, 3. Baron Rayleigh und Walter Ritz, auch unter dem Namen Ritzsches Variationsprinzip bekannt) besagt, dass für die Gesamtenergie E0 des Systems im Grundzustand
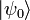 (also für den diesbezüglichen Erwartungswert des Hamilton-Operators
(also für den diesbezüglichen Erwartungswert des Hamilton-Operators 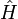 ) und für beliebige Wellenfunktionen/-Zustände
) und für beliebige Wellenfunktionen/-Zustände 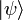 der Erwartungswert
der Erwartungswert 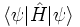 größer oder gleich (gleich im Fall der exakten Grundzustandswellenfunktion) der Grundzustandsenergie des Systems ist.
größer oder gleich (gleich im Fall der exakten Grundzustandswellenfunktion) der Grundzustandsenergie des Systems ist.Voraussetzung ist, dass der Hamiltonoperator nach unten beschränkt ist und an der unteren Grenze des Spektrums einen nicht entarteten Punkt-Spektralwert („Grundzustand“) besitzt. Man kann ähnliche Sätze aber leicht auch für andere Fälle beweisen.
Das bedeutet, dass die Probe-Wellenfunktion von der exakten Grundzustandsfunktion erheblich abweichen kann, aber ihr um so ähnlicher wird, je niedriger die berechnete Gesamtenergie ist. Da die meisten Probleme in der Quantenmechanik (abgesehen von speziellen Fällen, wie dem freien Teilchen, dem Teilchen im Kasten, dem Starren Rotator, dem harmonischen Oszillator und dem Wasserstoffatom) keine geschlossenen, exakten Lösungen haben, muss man zur Lösung der Schrödingergleichung für diese Systeme auf Näherungsverfahren zurückgreifen, wobei das Rayleigh-Ritz-Prinzip, weil man die exakte Funktion nicht kennt und auch kein kleiner Parameter involviert ist, im Allgemeinen „gute Intuition“ erfordert.
Beispiele für Schrödinger-Gleichungen mit nicht-exakten Lösungen sind der anharmonische Oszillator oder Mehrelektronensysteme wie Moleküle oder Festkörper.
Ritz-Verfahren
Das Ritzsche Variationsverfahren wendet obigen Satz direkt an. Dazu nutzt man eine Familie von Testwellenfunktionen, die über einen Satz von Parametern β variiert werden. So kann man etwa eine (nicht notwendig beschränkte) Basis
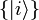 wählen und die Testwellenfunktion als Linearkombination darstellen:
wählen und die Testwellenfunktion als Linearkombination darstellen:Oder man wählt eine Familie von Funktionen, die über einen Parameter variiert werden, wie etwa Gauß-Kurven mit verschiedener Breite β:
Nun setzt man diese Funktionen in obigen Ausdruck ein und sucht den minimalen Wert von
![\langle H\rangle[\psi_\beta]](/pictures/dewiki/98/b8eb2140cc3a5444537b35c1177c1185.png) . Im einfachsten Fall kann dies durch Differentiation nach dem Parameter β geschehen:
. Im einfachsten Fall kann dies durch Differentiation nach dem Parameter β geschehen:Löst man diese Gleichung, so erhält man für β einen Wert, für den die Grundzustandsenergie minimiert wird. Mit diesem Wert hat man dann eine Näherungslösung, weiß aber nicht, wie gut der Ansatz wirklich ist (z. B. sind Gaußfunktionen für das Wasserstoffatom ganz schlecht), so dass man von „unkontrollierten Verfahren“ spricht. Immerhin kann man den Minimalwert als „beste Annäherung“ an die tatsächliche Grundzustandsenergie benutzen.
Zum Beweis
Der Hamiltonoperator wird in einer Eigenbasis dargestellt, wobei man der Einfachheit halber ein „diskretes Spektrum“ voraussetzt. Dann wird der Erwartungswert bezüglich der Testfunktion abgeschätzt:
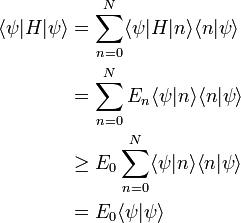
In der Praxis wählt man Testfunktionen mit einem oder mehreren freien Parametern, und variiert dann den Rayleigh-Quotienten
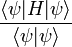 nach diesen. Das Minimum dieser Variation ist dann die beste Abschätzung für die Grundzustandsenergie E0 und es gilt:
nach diesen. Das Minimum dieser Variation ist dann die beste Abschätzung für die Grundzustandsenergie E0 und es gilt: 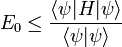 .
.Siehe auch
Wikimedia Foundation.

![E_0 \le \langle\hat H\rangle[\psi]\,:=\,\frac{\langle\Psi|\hat H|\Psi\rangle}{\langle\Psi|\Psi\rangle}](/pictures/dewiki/52/4641c5a0cf3fd5f16d3dfe268ed0c0aa.png)
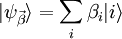
![\psi_{\beta}(x)=\frac{1}{\beta\sqrt{2\pi}}\cdot\exp\left[-\frac{x^2}{2\beta^2}\right]](/pictures/dewiki/97/a08723345187cc7495a551c85a4cfa32.png)
![\frac{\mathrm{d}}{\mathrm{d}\beta}\langle H\rangle[\psi_\beta]=0](/pictures/dewiki/100/dbf28e1db638f3889923f9f129fe0a6b.png)