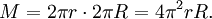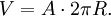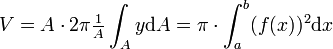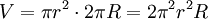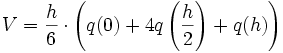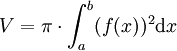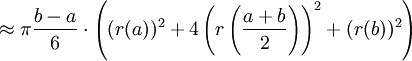- Rotationsvolumen
-
Rotationskörper werden in der Geometrie Körper genannt, die durch Rotation einer erzeugenden Kurve um eine Rotationsachse gebildet werden. Die Kurve liegt dabei in einer Ebene, und auch die Achse liegt in ebenderselben. Die Kurve schneidet die Achse nicht, berührt sie höchstens. Ein bekannter Rotationskörper ist der Torus. Er wird durch die Rotation eines Kreises gebildet. Auch Körper wie Zylinder und Hohlzylinder zählen zu den Rotationskörpern.
Das Volumen und die Oberfläche werden mit den so genannten Guldinschen Regeln (benannt nach dem Mathematiker und Astronomen Paul Guldin) errechnet. Bereits in der Antike waren diese als Baryzentrische Regeln bzw. Zentrobarische Regel bekannt und wurden vom griechischen Mathematiker Pappos von Alexandria beschrieben.
Inhaltsverzeichnis
Berechnung des Volumens eines Rotationskörpers
Rotation um x-Achse
Für einen Rotationskörper, der durch Rotation der Fläche, welche durch den Graphen der Funktion f im Intervall [a,b], der x-Achse und den beiden Geraden x = a und x = b begrenzt wird, um die x-Achse entsteht, lautet die Formel zur Volumenberechnung:
Rotation um y-Achse
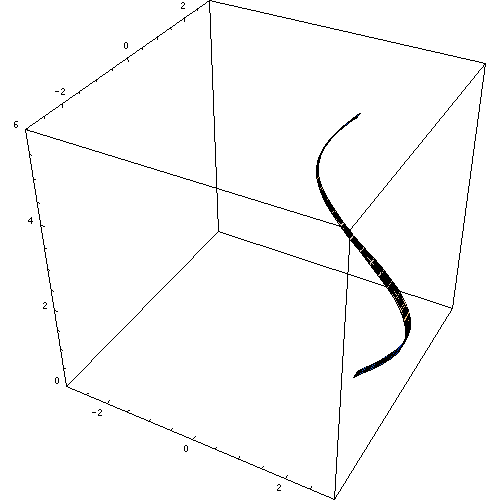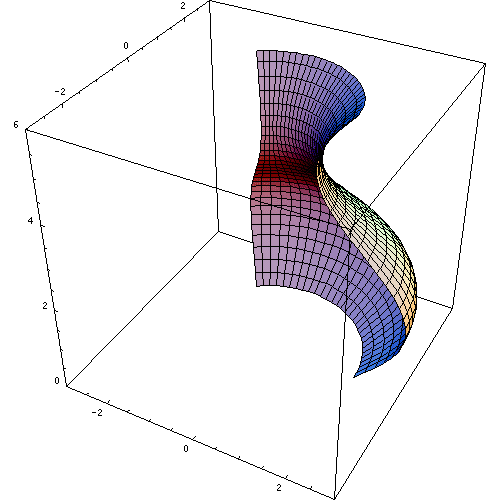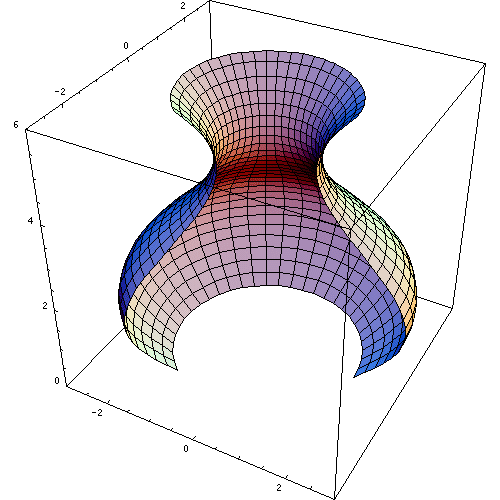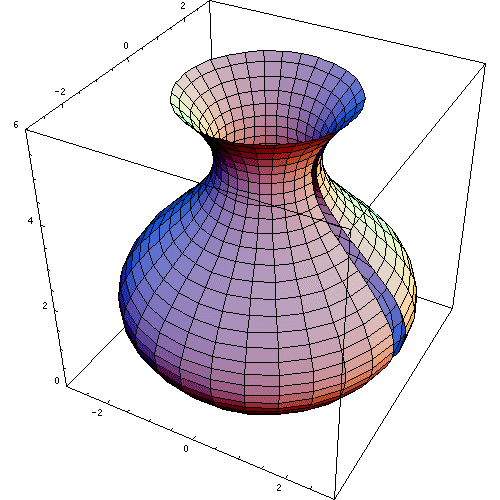
Bei Rotation (um die y-Achse) der Fläche, welche durch den Graphen der Funktion f im Intervall [a,b], der y-Achse und den beiden Geraden y = f(a) und y = f(b) begrenzt wird, muss man y = f(x) umformen zur Umkehrfunktion x = f − 1(y). Diese existiert, wenn f stetig und streng monoton ist. Falls nicht (wie z.B. im Bild rechts oben), lässt sich f vielleicht in Abschnitte zerlegen, in denen f jeweils stetig und streng monoton ist. Die zu diesen Abschnitten gehörenden Volumina müssen dann separat berechnet und aufaddiert werden.
Wenn man hier x = f − 1(y) substituiert, erhält man für das Volumen um die y-Achse
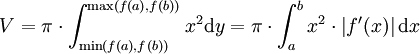 .
.
Der Absolutwert von f' und die min/max Funktionen in den Integralgrenzen sichern ein positives Integral.
Bei Rotation (um die y-Achse) der Fläche, welche durch den Graphen der Funktion f im Intervall [a,b], der x-Achse und den beiden Geraden x = a und x = b begrenzt wird, gilt die Formel:
Guldinsche Regeln
Die beiden guldinschen Regeln verkürzen Oberflächen- und Volumenberechnungen von Rotationskörpern enorm, falls sich die Linien- oder Flächenschwerpunkte der rotierenden Objekte unter Ausnutzen der Symmetrien der jeweiligen Aufgabe einfach erkennen lassen (s.u. Torus Beispiele).
Bezeichnungen:
- M = Oberfläche
- V = Rauminhalt
- L = Länge der erzeugenden Linie (Profillinie)
- A = Flächeninhalt der erzeugenden Fläche
- R = Radius des Schwerpunktkreises
- r = Radius des rotierenden Kreises (Torus-Beispiele)
Erste Regel
Die Mantelfläche M eines Rotationskörpers, dessen Rotationsachse die erzeugende Linie nicht schneidet, ist gleich dem Produkt aus der Länge der erzeugenden Linie (Profillinie) und dem Umfang des Kreises (Schwerpunktkreis), der durch die Rotation des Schwerpunktes der Profillinie erzeugt wird:
Ausgedrückt in Abhängigkeit von der Funktion f(x) der erzeugenden Linie ergibt das:
Bei Rotation um die x-Achse
Mit
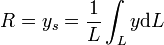 als y-Koordinate des Linienschwerpunktes der Linie L und ihrem Linienelement dL findet man
als y-Koordinate des Linienschwerpunktes der Linie L und ihrem Linienelement dL findet manwas das gesuchte Ergebnis darstellt, wenn noch
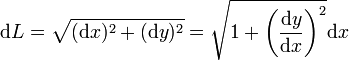 mit den x-Intervallgrenzen [a , b] eingesetzt wird.
mit den x-Intervallgrenzen [a , b] eingesetzt wird.Bei Rotation um die y-Achse
Wie oben bei der Volumenberechnung muss auch hier gegebenenfalls die Rechnung für die stetigen und streng monotonen Abschnitte von f(x), in denen die Umkehrfunktion existiert, separat durchführt werden.
Beispiel: Oberfläche eines Torus:
Siehe auch: Mantelfläche
Zweite Regel
Das Volumen eines Rotationskörpers ist gleich dem Produkt aus dem Flächeninhalt der erzeugenden Fläche und dem Umfang des Kreises, der durch die Rotation des Schwerpunktes dieser Fläche erzeugt wird:
Im Fall der Rotation um die x-Achse einer Fläche zwischen f(x), der x-Achse und den Grenzen x=a und x=b ergibt sich das Volumen ausgedrückt durch f(x) mit R als Flächenschwerpunkt zu
mit
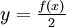 und dA = f(x)dx.
und dA = f(x)dx.Beispiel: Volumen eines Torus:
Keplersche Fassregel
Die Keplersche Fassregel gibt
als Näherungswert für das Volumen eines Körpers, dessen Querschnitt an drei Stellen bekannt ist, an. Ist der Körper ein Rotationskörper, so gilt bei Rotation um die x-Achse:
Für bestimmte Rotationskörper wie
- Kegel,
- Kegelstumpf,
- Zylinder,
- Rotationsparaboloid,
- Rotationshyperboloid,
- Rotationsellipsoid,
- und Kugel
gibt diese Formel das genaue Volumen an.
Weblinks
- Rotationskörper, Ronny Harbich, 2003
- Was ist Rotationssymmetrie?
- Das Ei als Rotationskörper
Wikimedia Foundation.

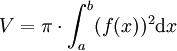
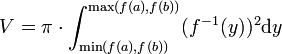
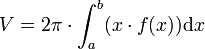
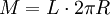
![M = 2\pi\int_a^b f(x)\sqrt{1+\left[f'(x)\right]^2}\mathrm{d}x.](/pictures/dewiki/49/14e855fe0e4be3aa9a85e1efeecb6d4e.png)
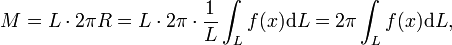
![M = 2\pi\int_{\min(f(a),f(b))}^{\max(f(a),f(b))} f^{-1}(y)\sqrt{1+\left[\left(f^{-1}(y)\right)'\right]^2}\mathrm{d}y.](/pictures/dewiki/50/23ec97079e0e22f864dc43082884045a.png)