Roy's Identität

Roys Identität ist ein bedeutender Satz innerhalb der Mikroökonomie. Benannt wurde dieser Satz nach dem französischen Ökonom René Roy. Roys Identität beruht auf Shephards Lemma um über eine Marshallsche Nachfragefunktion eine normale Nachfragefunktion der Ableitung der indirekten Nutzenfunktion gegenüberzustellen.

Mathematische Herleitung

Unter der Annahme die Indirekte Nutzenfunktion sei

$\psi\ ( e(p, u), p) = u$

Die erste Ableitung nach p_i ergibt:

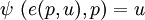
$\frac{ \partial \psi\ [e(u,p),p]}{\partial m} \frac{\partial e(u,p)}{\partial p_i} + \frac{\partial \psi\ [e(u,p),p]}{\partial p_i} = 0$.

Durch Umformung erhält man Roys Identität

$\frac{\partial e(u,p)}{\partial p_i}=-\frac{\frac{\partial \psi\ [e(u,p),p]}{\partial p_i}}{\frac{\partial \psi\ [e(u,p),p]}{\partial m}}=x_i(m,p)$

Siehe auch

• Slutsky-Zerlegung

Literatur

• Roy, René (1947).: "La Distribution du Revenu Entre Les Divers Biens," Econometrica, 15, 205-225.
• Marshall, A.: Principles of Economies, 8. Aufl., London 1920;

Weblinks

• Beweis der Roys Identiät