Envelope-Theorem

Der Umhüllungssatz oder auch Envelope-Theorem ist ein grundlegender Satz der Variationsrechnung, der häufig Anwendung in der Mikroökonomie findet. Er beschreibt, wie sich die Zielfunktion eines parametrisierten Maximierungsproblems bei Änderung der Parameter verhält.

Man betrachte folgendes mit dem Vektor q parametrisierte Maximierungsproblem:

$v(q)=\max_x f(x,q)\,$

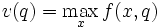
mit den Nebenbedingungen

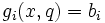$g_i(x,q)=b_i \,$ für $i\in I$.

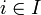Angenommen, in einer Umgebung von q ^* ist v(q) wohldefiniert und die Lösungsfunktion x(q) differenzierbar.

Seien weiterhin λ_i die Werte der Lagrange-Multiplikatoren für die Nebenbedingungen an der Stelle q ^* . Der Umhüllungssatz besagt dann, dass für alle j

$\left.\frac{\partial v(q)}{\partial q_j}\right|_{q=q^*}=\left.\frac{\partial f(x,q)}{\partial q_j}\right|_{x=x(q^*),q=q^*}\, - \, \sum_{i\in I} \lambda_i\left.\frac{\partial g_i(x,q)}{\partial q_j}\right|_{x=x(q^*),q=q^*}$

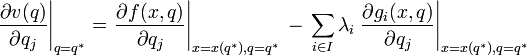
Im Falle eines Maximierungsproblems ohne Nebenbedingung ergibt sich, dass bei der Berechnung des Effektes erster Ordnung einer Variation von q auf v(q) = f(x(q),q) die Änderung von x keinen Einfluss hat.

v(q) ist Einhüllende der Kurvenschar 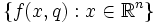$\{f(x,q):x\in\mathbb{R}^n\}$, daher der Name des Satzes.

Anwendung

Eine Anwendung findet sich in der Mikroökonomie. Dort kann man den Umhüllungssatz sowohl in der Theorie der Unternehmungen als auch in der Theorie der Haushalte einsetzen.

Im Bereich der Theorie der Unternehmungen bezeichnet y(x) die Produktionsmenge in Abhängigkeit vom Input x, so ergibt sich, indem man q = (p,w) als den Preisvektor für Output- und Inputgut setzt, und mit f als Produzentengewinn, f(x,p,w) = py(x) − wx, Hotellings Lemma. Es ist allerdings auch möglich, das Envelope-Theorem in der Kostenminimierung einzusetzen. Dies funktioniert analog zu Hotelling's Lemma.

In der Theorie der Haushalte wird das Envelope-Theorem im Zusammenhang mit indirekten Nutzenfunktionen verwendet. Dabei kann leicht mittels Roy's Identität analysiert werden, was bei einer Einkommens- oder einer Preisveränderung passiert. Dafür wird die indirekte Nutzenfunktion partiell abgeleitet nach Einkommen und Preis.

Literatur

Mas-Colell, Andreu; Whinston, Michael; & Green, Jerry (1995). Microeconomic Theory. Oxford: Oxford University Press. ISBN 0195073401 Breyer, Friedrich (2004). Mikroökonomik - Eine Einführung. Berlin: Springer Verlag. ISBN 3540211039