Rubiks Rache

Rubiks Rache in einem Chaoszustand

Rubiks Rache oder auch Rubik’s Master Cube ist ein würfelförmiges Geduldsspiel. Es handelt sich um eine etwas größere und schwierigere Variante des Rubik’s Cube, ebenfalls mit sechs Farben, aber mit drei anstatt zwei Drehachsen in jeder Raumrichtung. Dadurch erhöht sich die Anzahl der Segmente auf jeder der sechs Seitenflächen von neun auf 4×4 = 16.

Dabei wirkt es, als wäre die Oberfläche in 56 Würfelchen unterteilt, die mittels 90-Grad-Drehungen um die neun Drehachsen die Position zueinander verändern. Ziel des Geduldspiels ist, ebenso wie bei dem klassischen Zauberwürfel, den Master Cube aus einer ungeordneten Stellung heraus in seinen geordneten Grundzustand zu überführen, bei dem alle Segmente einer Seitenfläche die gleiche Farbe haben.

Geschichte

Die 4×4×4-Version des Zauberwürfels wurde 1981 von dem ungarischen Mathematiker Peter Sebestény erfunden und zum Patent angemeldet. Die Nutzungsrechte des Patents verkaufte er an die in den USA ansässige Ideal Toy Company.

Die Achsen, die den Würfel zusammenhalten und den Drehmechanismus realisieren, sind in vier Teile gespaltet und werden durch einen Kern zusammengehalten. Die Idee, die Achsen auf diese Weise zu teilen, war neu und hat die Erteilung des Patentes ermöglicht.

Ideal Toy hat den Viererwürfel zusammen mit dem „Rubik’s“-Warenzeichen vermarktet, ihn in den USA als „Rubik’s Revenge“ und in Europa als „Rubik’s Master Cube“ verkauft. In den 1980er-Jahren war der Markt bald mit verschiedenen Puzzle-Varianten derartig gesättigt, dass Ideal Toy nach wenigen Jahren die Produktion des Viererwürfels einstellte. Die Umsetzung und Vermarktung anderer Drehmechanismen, die nicht patentgeschützt waren, haben dafür gesorgt, dass der Vierer-Würfel bis heute hergestellt und verkauft wird.

Den Weltrekord im Speedcubing hält der Niederländer Erik Akkersdijk mit 40.05 Sekunden bei den Aachen Open 2009.^[1]

Kombinationen

Der Master Cube besteht aus 56 beweglichen Teilen, also deutlich mehr als die 20 des 3×3×3-Würfels. Ebenso wie bei diesem handelt es sich nicht um einen Würfel, dessen Oberfläche zerlegt ist, sondern nur um Würfel-Segmente. Im Einzelnen sind das:

Mittelteile

• mit je einer Farbe, 24 Stück, vier pro Farbe
• Die Mittelteile sind anders als beim klassischen Zauberwürfel nicht fixiert, weshalb die richtige Lage der Steine ebenso wie bei dem Pocket Cube an den Ecksteinen abgelesen werden muss.
• Die Mittelteile können unabhängig voneinander die Positionen tauschen, aber da es vier pro Farbe gibt, die sich nicht unterscheiden lassen, gelangt man zu 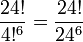$\frac{24!}{4!^6}= \frac{24!}{24^6}$ Kombinationen der Mittelteile.

Kantenteile

• mit je zwei Farben, 24 Stück, zwei pro Farbkombination
• Die Orientierung der Kantenteile hängt vollständig von ihrer Position im Würfel ab. Obwohl es von jeder Sorte zwei Stück gibt, können sie nicht (irrtümlich) den Platz tauschen, da sich dann auch die Orientierung ändert und die Farben genau falsch liegen.
• Die Kantenteile können unabhängig voneinander die Positionen tauschen, es gibt nur eine korrekte Stellung und sie können nicht die Orientierung ändern, das führt zu 24! Kombinationen der Kantenteile.

Eckteile

• je drei Farben, acht Stück, jeweils eins pro Farbkombination
• Die Eckteile verhalten sich genauso wie die des Dreier-Würfels. Sie können unabhängig die Positionen tauschen, und jede Ecke hat drei verschiedene Orientierungen, die sich aber gegenseitig beeinflussen: Konstuktionsbedingt werden nur ein Drittel der theoretisch möglichen Kombinationen angenommen.
• Da die Mittelteile beweglich sind, hat der Master Cube ebenso wie der Pocket Cube keine festgelegte Orientierung im Raum: Eine beliebige Ecke kann stets als richtig und damit als Referenzpunkt angesehen werden, auf dem die weitere Lösung beruht.
• Dies führt zu 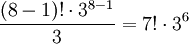$\frac{(8-1)! \cdot 3^{8-1}}{3} = 7! \cdot 3^6$ Kombinationen der Eckteile.

Insgesamt gibt es damit $\frac{24!}{24^6} \cdot 24! \cdot 7! \cdot 3^6 = \frac{23!}{8^4} \cdot 23! \cdot 7! \cdot 3^2 = 23!^2 \cdot 9! \cdot 2^{-15} =$

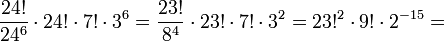
7.401.196.841.564.901.869.874.093.974.498.574.336.000.000.000^[2] 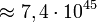$\approx 7,4 \cdot 10^{45}$ -viele Stellungen, die der Master Cube annehmen kann. Das sind weit mehr als 10²⁰-mal so viele wie beim Zauberwürfel.

Siehe auch Kombinatorik, Fakultät

Schwierigkeitsgrad

Obwohl der Master Cube sehr viel mehr mögliche Stellungen als der Dreier-Würfel hat, ist er an sich nicht schwieriger. Natürlich müssen mehr Steine sortiert werden, da aber mit einer Drehung maximal etwa 28,6 % der Teile bewegt werden, im Gegensatz zu 40 % bei der klassischen Variante, beeinflussen sich die Teile gegenseitig weniger.

Insbesondere die Mittelteile lassen sich mit kurzen und einfachen Zugfolgen sortieren. Jede bekannte Lösungsstrategie für die Eckteile kann genauso beim Master Cube verwendet werden. Anders bei den Kantenteilen: Hier werden z.T. neue Zugfolgen benötigt, da das Verhalten einzelner Kantensteine wenig Entsprechung im Dreier-Würfel hat. Paare, also zwei nebeneinander liegende Kantensteine, können jedoch genauso wie einzelne Kantensteine beim Dreier-Würfel sortiert werden.

Lösungsstrategien

Weit verbreitet ist der Ansatz, zuerst die Mittelteile zu sortieren und die Kanten zu paaren. Von jetzt an werden die mittleren Drehachsen nicht mehr benutzt, wodurch sich der Master Cube wie der Dreier-Würfel verhält. Jede bekannte Strategie für diesen führt dann auch zur Lösung des Master Cube, bis auf eine Ausnahme: Es kann passieren, dass ein Kantenpaar falsch orientiert ist. Wie oben dargestellt, müssen dann die beiden nebeneinander liegenden Kantenteile die Position tauschen, was nur geht, indem auch zwei Mittelteile, von denen ja immer vier gleich sind, den Platz tauschen.

Es gibt aber auch diverse weitere Möglichkeiten, den Master Cube zu lösen.

Notation

Eine graphische Notation wird beim Rubik’s Revenge eher selten benutzt, weit verbreitet ist eine Weiterführung der Buchstaben-Notation. 90-Grad-Drehungen der Außenseiten im Uhrzeigersinn werden wie beim Dreier-Würfel mit Großbuchstaben bezeichnet, gemäß ihrer Lage vorne, hinten, oben, unten, links oder rechts mit V,H,O,U,L,R. Entsprechend werden Drehungen im Uhrzeigersinn der innenliegenden Ebenen mit kleinen Buchstaben versehen: v,h,o,u,l,r. Weiterhin bedeutet r ^{− 1} eine Drehung gegen den Uhrzeigersinn um 90 Grad und r² eine 180-Grad-Drehung der inneren rechten Ebene. Dabei bezieht sich der Uhrzeigersinn auf die zu drehende Ebene, während beispielsweise h und H die gleiche Drehorientierung haben, ist sie zwischen h und f genau umgekehrt.

Bemerkungen

• Es ist möglich, mit dem Master Cube sowohl den Pocket Cube als auch den klassischen Zauberwürfel zu emulieren. Im ersten Fall dürfen nur die mittleren Drehachsen genutzt werden, im zweiten nur die äußeren.
• Der Master Cube kann auseinandergenommen und wieder zusammengebaut werden. Das gilt für die Versionen aller Hersteller, allerdings ist bei manchen dazu Werkzeug wie ein Schraubendreher notwendig. Auch müssen manchmal ein paar Aufkleber entfernt werden, um an den Mechanismus zu gelangen.

Literatur

Einführungen und Anleitungen

• Douglas R. Hofstadter: Vom Zauber des Zauberwürfels. In: Mathematische Spielereien, Spektrum der Wissenschaft. Ausgabe Mai 1981, Heidelberg, S. 16ff. ISSN 0170-2971.
• Kurt Endl: Le Rubik's cube, enigme du siècle. Würfel-Verlag, Gießen 1981, ISBN 3-923210-15-9.
• Jérôme Jean-Charles: Master Rubik’s Cube. Denoël, Paris 1982, ISBN 2-207-22790-1.
• Michael Reid: Mastering Rubik’s Revenge. Simon & Schuster, New York 1982, ISBN 0-671-45952-4 (formal falsche ISBN).
• Kurt Endl: Rubik’s Master Cube. Würfel-Verlag, Giessen 1982, ISBN 3-923210-50-7.
• Kurt Endl: Die gemeinsame Strategie für alle Rubik'schen Würfel. Würfel-Verlag, Giessen 1983, ISBN 3-923210-80-9.

Mathematik

Die folgenden Titel befassen sich mit den mathematischen Eigenschaften des Zauberwürfels, enthalten aber auch Anleitungen, die eventuell leichter nachzuvollziehen sind als die informellen Einführungen:

• David Singmaster: Notes on Rubik’s Magic Cube. 5. Auflage. Singmaster, London 1980, ISBN 0-907395-00-7.
• Alexander H. Frey jr., David Singmaster: Handbook of Cubik Math. Enslow, Hillside 1982, ISBN 0-89490-060-9.
• Christoph Bandelow: Einführung in die Cubologie. Vieweg, Braunschweig und Wiesbaden 1981, ISBN 3-528-08499-5; erweiterte englische Fassung: Christoph Bandelow: Inside Rubik’s Cube and Beyond. Birkhäuser, Basel und Boston 1982, ISBN 3-7643-3078-3.
• Ernő Rubik, Tamas Varga, Gerzson Keri, Gyorgy Marx, Tamas Vekerdy: Rubik’s Cubic Compendium. Oxford University Press, London 1987, ISBN 0-19-853202-4.

Weblinks

• Rubik’s-Revenge-Lösung von Chris Hardwick
• Rubik’s-Revenge-Lösung illustriert
• Würfelmuster

Einzelnachweise

1. ↑ Offizielle Ergebnisse der World Cube Association
2. ↑ Jaaps-Master-Cube-Seite (englisch)