Satz von Immerman und Szelepcsény
- Satz von Immerman und Szelepcsény
-
Der Satz von Immerman und Szelepcsényi ist ein Satz aus der Komplexitätstheorie und besagt, dass die Klasse NSPACE unter dem Komplement abgeschlossen ist.
Lange nahm man an, dass die Klasse NSPACE genauso wie die Klasse NTIME nicht unter dem Komplement abgeschlossen sei, bis 1988 Immerman und Szelepcsényi unabhängig voneinander den Beweis erbrachten.
Formale Definition
Sei 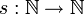 eine bandkonstruierbare Funktion mit
eine bandkonstruierbare Funktion mit 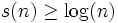 . Dann ist NSPACE(S) = Co-NSPACE(S).
. Dann ist NSPACE(S) = Co-NSPACE(S).
Siehe auch
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Satz von Immerman und Szelepcseny — Der Satz von Immerman und Szelepcsényi ist ein Satz aus der Komplexitätstheorie und besagt, dass die Klasse NSPACE unter dem Komplement abgeschlossen ist. Lange nahm man an, dass die Klasse NSPACE genauso wie die Klasse NTIME nicht unter dem… … Deutsch Wikipedia
Aufwandsklasse — Eine Komplexitätsklasse ist in der Komplexitätstheorie eine Kategorie von Problemen beziehungsweise von Algorithmen, zusammengefasst nach einem gemeinsamen Maß der Komplexität. Definiert wird eine Komplexitätsklasse durch eine obere Schranke für… … Deutsch Wikipedia
Aufwandsklassen — Eine Komplexitätsklasse ist in der Komplexitätstheorie eine Kategorie von Problemen beziehungsweise von Algorithmen, zusammengefasst nach einem gemeinsamen Maß der Komplexität. Definiert wird eine Komplexitätsklasse durch eine obere Schranke für… … Deutsch Wikipedia
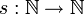 eine bandkonstruierbare Funktion mit
eine bandkonstruierbare Funktion mit 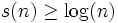 . Dann ist NSPACE(S) = Co-NSPACE(S).
. Dann ist NSPACE(S) = Co-NSPACE(S).