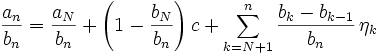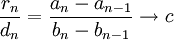- Satz von Stolz-Cesaro
-
Der Satz von Stolz bzw. Satz von Stolz-Cesàro handelt von Grenzwerten in der Mathematik. Er ist benannt nach dem österreichischen Mathematiker Otto Stolz (1842–1905) und dem italienischen Mathematiker Ernesto Cesàro (1859–1906).
Inhaltsverzeichnis
Satz
Sind
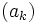 und
und 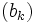 mit
mit 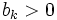 Folgen wobei letztere streng monoton ist und unbeschränkt wächst.
Folgen wobei letztere streng monoton ist und unbeschränkt wächst.Dann folgt aus der Existenz des Grenzwertes der Differenzenquotienten
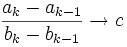 für
für 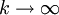
die Existenz des Grenzwerts der Quotienten zum selben Wert,
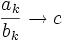 .
.Beweis
Nach der Annahme der Konvergenz der Differenzenquotienten existiert für jedes
 ein
ein 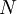 , so dass für alle
, so dass für alle  der Differenzenquotient zum Index
der Differenzenquotient zum Index 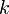 in der Umgebung
in der Umgebung 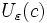 liegt. Es gibt also für jedes
liegt. Es gibt also für jedes 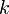 ein
ein 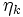 mit
mit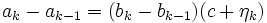 ;
;
für
 gilt
gilt 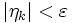 .
.Summiert man diese Beziehungen nach
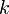 von
von 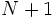 bis
bis 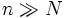 , so erhält man die Gleichung
, so erhält man die Gleichung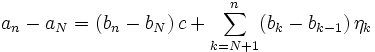 .
.
Somit gilt für den Quotienten der Folgenglieder
Der erste Summand der rechten Seite konvergiert gegen Null, da die Folge
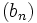 unbeschränkt wächst. Aus demselben Grunde konvergiert der zweite Summand gegen
unbeschränkt wächst. Aus demselben Grunde konvergiert der zweite Summand gegen  . Aufgrund der Monotonie der Folge
. Aufgrund der Monotonie der Folge 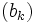 gilt für den dritten Summanden
gilt für den dritten Summanden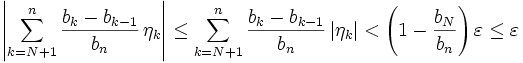 .
.
Man kann nun ein
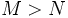 finden, so dass für alle
finden, so dass für alle  auch in den ersten zwei Summanden die Differenz zum Grenzwert durch
auch in den ersten zwei Summanden die Differenz zum Grenzwert durch  beschränkt ist, für alle
beschränkt ist, für alle 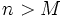 erhält man dann die Abschätzung
erhält man dann die Abschätzung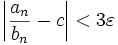 ,
,
somit konvergiert die Folge der Quotienten gegen
 .
.Zur Umkehrung
Die Umkehrung des obigen Satzes ist im Allgemeinen falsch. Betrachtet man die beiden Folgen
(ak) = (10,10,100,100,1000,1000,...)
(bk) = (10,11,100,101,1000,1001,...)
Dann gilt
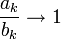 . Die Folge
. Die Folge 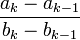 hat jedoch keinen Grenzwert.
hat jedoch keinen Grenzwert.Verallgemeinerung
Gegeben seien zwei weitere Folgen
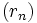 und
und 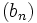 derart, dass
derart, dass 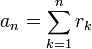 und
und 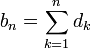 . Weiterhin sei
. Weiterhin sei 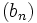 streng monoton und unbeschränkt wachsend.
streng monoton und unbeschränkt wachsend.Aus
folgt dann
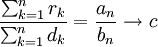 .
.
Die oben genannten Voraussetzungen werden erfüllt von
- der harmonischen Reihe
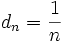 , und
, und - jeder Reihe, deren Glieder einen positiven Grenzwert besitzen, wie
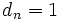 , d. h.
, d. h. 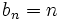 , oder gar
, oder gar - jeder Reihe, deren Glieder selbst wachsen, wie
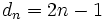 , d. h.
, d. h. 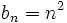 .
.
Bemerkungen
Ein Spezialfall ist der Cauchysche Grenzwertsatz.
In gewisser Weise stellt der Satz von Stolz ein Äquivalent für die Grenzwertberechnung bei Folgen zu der Regel von L’Hospital zur Grenzwertberechnung bei differenzierbaren Funktionen dar.
Weblinks
Wikimedia Foundation.