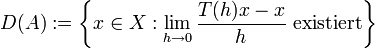- Satz von Stone
-
Eine stark stetige Gruppe ist eine Familie
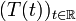 von beschränkten linearen Operatoren von einem reellen oder komplexen Banachraum X in sich und ist ein Spezialfall einer stark stetigen Halbgruppe. Stark stetige Gruppen werden bei der Untersuchung von partiellen Differentialgleichungen angewandt, die einen reversiblen Vorgang beschreiben.
von beschränkten linearen Operatoren von einem reellen oder komplexen Banachraum X in sich und ist ein Spezialfall einer stark stetigen Halbgruppe. Stark stetige Gruppen werden bei der Untersuchung von partiellen Differentialgleichungen angewandt, die einen reversiblen Vorgang beschreiben.Inhaltsverzeichnis
Definition
Seien X ein Banachraum und
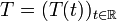 eine Familie beschränkter linearer Operatoren
eine Familie beschränkter linearer Operatoren 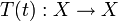 für
für 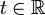 . Gilt
. Gilt- T(0) = I,
- T(s + t) = T(s)T(t) für alle
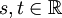 und
und 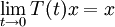 für alle
für alle  ,
,
wird diese Familie stark stetige Gruppe genannt.
Infinitesimaler Erzeuger
Der (infinitesimale) Erzeuger (A,D(A)) ist gegeben durch
und
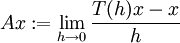 für
für 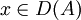 .
.
Folgerungen
- Erzeugen (A,D(A)) eine stark stetige Halbgruppe
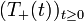 mit
mit 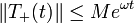 und ( − A,D(A)) eine stark stetige Halbgruppe
und ( − A,D(A)) eine stark stetige Halbgruppe 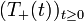 mit
mit 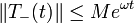 für ein
für ein 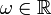 , M > 0 und alle t > 0, so ist (A,D(A)) der Erzeuger einer stark stetigen Gruppe
, M > 0 und alle t > 0, so ist (A,D(A)) der Erzeuger einer stark stetigen Gruppe 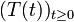 mit T(t) = T + (t) für
mit T(t) = T + (t) für 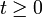 , T(t) = T − ( − t) für t < 0 und
, T(t) = T − ( − t) für t < 0 und 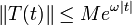 für
für 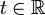 .
. - Sei (A,D(A)) ein dicht definierter, abgeschlossener Operator und es existiere
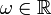 und M > 0, so dass
und M > 0, so dass 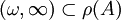 und
und 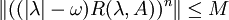 für alle λ > ω und alle
für alle λ > ω und alle 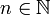 . Dann erzeugt (A,D(A)) eine stark stetige Gruppe
. Dann erzeugt (A,D(A)) eine stark stetige Gruppe 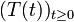 mit
mit 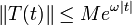 für alle
für alle 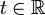 . Hierbei stehen R(λ,A) für die Resolvente und ρ(A) für die Resolventenmenge von A.
. Hierbei stehen R(λ,A) für die Resolvente und ρ(A) für die Resolventenmenge von A.
Satz von Stone
Marshall Harvey Stone veröffentlichte 1932 in den Annals of Mathematics folgenden Satz: Seien X ein Hilbertraum und T eine stark stetige Gruppe, wobei T(t) für alle
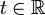 unitär ist. Dann existiert ein selbstadjungierter Operator A, so dass iA der Erzeuger von T ist. Umgekehrt erzeugt iA für jeden selbstadjungierten Operator A eine stark stetige Gruppe aus unitären Operatoren.
unitär ist. Dann existiert ein selbstadjungierter Operator A, so dass iA der Erzeuger von T ist. Umgekehrt erzeugt iA für jeden selbstadjungierten Operator A eine stark stetige Gruppe aus unitären Operatoren.Literatur
- Klaus-Jochen Engel, Rainer Nagel: One-parameter semigroups for linear evolution equations. Graduate Texts in Mathematics, 194. Springer-Verlag, New York, 2000. ISBN 0-387-98463-1.
- Tosio Kato: Perturbation Theory for Linear Operators. 2. Auflage. Springer-Verlag 1995, ISBN 354058661X.
- Ammon Pazy: Semigroups of Linear Operators and Applications to Partial Differential Equations. Applied Mathematical Sciences 44, Springer-Verlag, Berlin 1983, ISBN 3-540-90845-5.
Wikimedia Foundation.