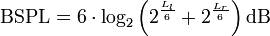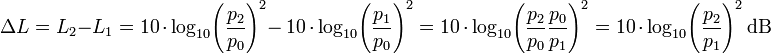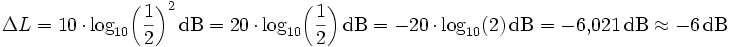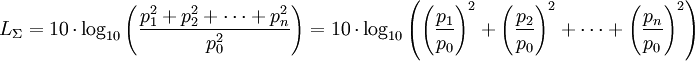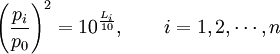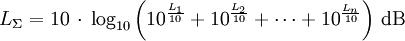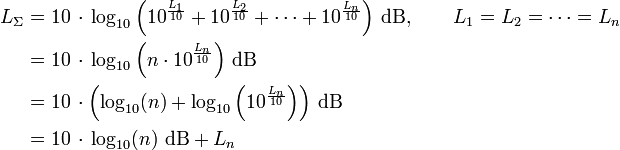Schallenergetische Addition

Schallgrößen
Schalldruck p Schalldruckpegel Lp Schallschnelle v Schallauslenkung ξ Schallbeschleunigung a Schallintensität I Schallleistung Pak Schallenergiedichte E Schallenergie Schallfluss q Schallimpedanz Z Schallgeschwindigkeit c

Der Schalldruckpegel ist ein logarithmisches Maß zur Beschreibung der Stärke eines Schallereignisses. Er gehört zu den Schallfeldgrößen. Häufig wird der Schalldruckpegel, obwohl dann physikalisch nicht eindeutig, auch einfach Schallpegel genannt.

Definition

Schallpegelmeßgerät

Der Schalldruckpegel L_p (L von engl. level: „Pegel“ und p von engl. pressure: „Druck“) beschreibt das logarithmierte Verhältnis des quadrierten Effektivwertes des Schalldrucks (Formelzeichen 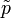$\tilde{p}$ mit der Einheit Pa für Pascal) eines Schallereignisses zum Quadrat eines Bezugswerts p₀. Das Ergebnis wird mit der Hilfsmaßeinheit Dezibel (Abkürzung dB) gekennzeichnet.

$L_p=10\, \log_{10}\left(\frac{{\tilde{p}}^2}{{p_0}^2}\right) \mathrm{dB} = 20\, \log_{10}\left(\frac{\tilde{p}}{p_0}\right) \mbox{dB}$.

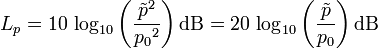Der Bezugswert für Luftschall wurde Anfang des 20. Jahrhunderts auf p₀ = 20 µPa = 2 · 10^-5 Pa festgelegt. Dieser Schalldruck wurde für die Hörschwelle des menschlichen Gehörs bei der Frequenz 1 kHz gehalten. Zwar stellte sich später heraus, dass dieser Wert für 1 kHz etwas zu niedrig angesetzt war, dennoch wurde er als Referenzwert p₀ beibehalten. Für die Angabe eines Schalldruckpegels in Wasser und anderen Medien ist ein Bezugswert von 1 µPa festgelegt. Als Pegelgröße kann der Schalldruckpegel sowohl positive (Schalldruck ist größer als Bezugswert) als auch negative (Schalldruck ist kleiner als Bezugswert) Werte annehmen.

Messung

Die Messung von Schalldrücken erfolgt mit Mikrofonen. Der messbare Pegelbereich beginnt nicht wesentlich unter 0 dB und endet bei einer Größenordnung von ca. 150 bis 160 dB.

Die Obergrenze liegt darin begründet, dass die Gesetze der linearen Akustik nur anwendbar sind, wenn die Luftdruckschwankungen deutlich kleiner sind als der Atmosphärendruck. Die durch die Druckschwankungen der Luft erzeugten adiabatischen Zustandsänderungen und somit die Beziehungen zwischen den Schallfeldgrößen verhalten sich nur dann linear. Für höhere Wechseldrücke sind Schallschnelle und Schalldruck dagegen nicht mehr sinusförmig.

Ein digitales Schalldruckpegelmessgerät

Die Richtcharakteristik von Mess-Mikrofonen zur Schalldruckbestimmung ist im Allgemeinen kugelförmig. Für so genannte binaurale Tonaufnahmen werden Kunstköpfe verwendet. Von einem binauralen Schalldruckpegel spricht man, wenn aus den beiden Schalldruckpegeln des linken und des rechten Ohrs ein Gesamtpegel gebildet wird. Für diese Größe hat sich in der Psychoakustik die Bezeichnung BSPL (binaural sound pressure level) etabliert. Die Bildung des BSPL wird gemäß dem sogenannten 6-dB-Lautheits-Gesetz^[1] nach folgender Formel durchgeführt:

$\mathrm{BSPL} = 6\cdot \log_2\left(2^{\frac{L_l}{6}}+2^{\frac{L_r}{6}}\right) \mathrm{dB}$

In dieser nur im Diffusfeld geltenden Formel stehen die Größen L_l und L_r für die Schalldruckpegel, die am linken bzw. am rechten Kunstkopfohr gemessen werden.

Wahrnehmung durch den Menschen

Der Schalldruckpegel ist eine technische und keine psychoakustische Größe. Ein Rückschluss von Schalldruckpegel auf die wahrgenommene Empfindung ist nur sehr eingeschränkt möglich. Ganz allgemein lässt sich sagen, dass eine Erhöhung bzw. Senkung des Schalldruckpegels tendenziell auch ein lauter bzw. leiser wahrgenommenes Schallereignis hervorruft. Als Faustformel gilt, dass 10 dB Unterschied etwa als doppelte bzw. halbe Lautstärke wahrgenommen wird.

Die Erkennbarkeit von Schalldruckpegeländerungen ist vom Ausgangspegel abhängig. "Das Gehör wird mit wachsendem Schalldruck immer empfindlicher gegen Amplitudenänderungen von Sinustönen. Bei einem niedrigen Pegel von 20 dB liegt der eben wahrnehmbare Modulationsgrad bei einem Wert von etwa 10%. Bei einem Pegel von 100 dB erreicht er etwa den Wert von 1%."^[2]

Hohe Schalldruckpegel verursachen Unbehaglichkeit und Schmerzempfindungen. Die Unbehaglichkeitsschwelle hängt stark von Art und Herkunft des Geräusches bzw. Lärms ab; die Schmerzschwelle liegt je nach Frequenzzusammensetzung des Geräusches zwischen 120 dB und 140 dB. Ist das Gehör Schalldrücken im Bereich der Schmerzschwelle ausgesetzt, sind bleibende Hörschäden selbst bei nur kurzer Einwirkzeit zu erwarten.

Wahrnehmung: Kurven gleicher Lautstärke

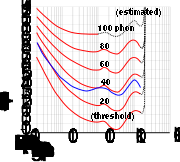
Die Abhängigkeit von wahrgenommener Lautstärke und Schalldruckpegel ist stark frequenzabhängig. Diese Frequenzabhängigkeit ist selbst wiederum schalldruckpegelabhängig, was bedeutet, dass für unterschiedliche Pegel unterschiedliche Frequenzabhängigkeiten bestehen. Sollen Aussagen über die Wahrnehmung eines Schallereignisses gemacht werden, muss daher die Frequenzzusammensetzung (Spektrum) des Schalls betrachtet werden. Darüber hinaus haben zeitlicher Verlauf sowie die Eigenschaft, sich über mehrere Frequenzgruppen zu erstrecken, einen Einfluss.

Um die wahrgenommene Lautstärke dennoch quantifizieren zu können, existieren die Größen bewerteter Schalldruckpegel, Lautstärkepegel und Lautheit. Lautstärkepegel (Maßeinheit Phon) und Lautheit (Maßeinheit sone) sind psychoakustische Größen, beschreiben also die Wahrnehmung von Schall, nicht dessen physikalische Eigenschaften. Nur durch psychoakustische Experimente (Hörversuche) ist die Definition solcher Größen möglich. Der bewertete Schalldruckpegel ist wiederum eine vereinfachte Darstellung, die aus diesen Erkenntnissen abgeleitet wurde: Der bewertete Schalldruckpegel wird ermittelt, indem ein gemessenes Spektrum im Frequenzbereich in schmalbandige Teile zerlegt wird und diese entsprechend der Frequenzabhängigkeit der Wahrnehmung gewichtet („bewertet“) werden. Durch energetische Aufsummierung dieser gewichteten Teilpegel ergibt sich dann der bewertete Gesamtpegel. Um diesen zu kennzeichnen, wird der jeweils verwendete Frequenzfilter hinter der dB-Angabe in Klammern ergänzt, z. B. 35 dB(A) bei Anwendung des A-Filters. Die Frequenzfilter gehen dabei grob vereinfachend von gleicher und konstanter Lautheit jeder im Schall enthaltenen Frequenzgruppe aus. Zudem werden die für diese Lautheit für sinusoidale Einzeltöne ermittelten Isophone (Kurven gleicher Lautstärke) für die schmalen Bänder verwendet. Der bewertete Schalldruckpegel leistet also eine psychoakustisch fehlerbehaftete, aber dennoch brauchbare und standardisierte Berücksichtigung der Frequenzabhängigkeit der menschlichen Lautstärkewahrnehmung und ist für akustische Grenzwerte in nahezu jeder gesetzlichen Bestimmung und jedem Standard maßgeblich. Welcher Frequenzfilter (A, B, C oder D) sinnvoller Weise verwendet wird, hängt vom Pegel des Gesamtgeräuschs ab, da bei jeder dieser Filter eine andere Isophone als Grundlage dient. Unabhängig vom vorliegenden Gesamtpegel hat sich allerdings überwiegend der A-Pegel durchgesetzt; bezüglich dieser Frage bestehen jedoch auch nationale Unterschiede.

Digitale Schallpegelmessgeräte können in der Regel auch die psychoakustischen Größen Lautheit und Lautstärkepegel anzeigen. Diese beiden Werte werden dafür ständig aus dem gemessenen Spektrum errechnet.

Dauerschallpegel

Als äquivalenter Dauerschallpegel L_eq wird der über die Messzeit gemittelte Schalldruckpegel bezeichnet. Der äquivalente Dauerschallpegel wird in der Regel zur Ermittlung des bewerteten Schadruckpegels genutzt.

Es wird zwischen folgenden Mittelungen unterschieden:

• energie-äquivalente Mittelung nach DIN 45 641 (L_eq)
• Mittelung nach DIN 45 643 entsprechend dem Fluglärmgesetz (L_eq4). In diese Mittelung fließen Häufigkeit, Dauer und die Stärke der einzelnen Fluglärmschallereignisse ein.

Schalldruckpegel und Schalldruck diverser Schallquellen

Situation bzw. Schallquelle	Entfernung von Schallquelle bzw. Messort	Schalldruck p  in Pascal	A-bewerteter Schalldruckpegel LpA in dB re 20 µPa
Düsenflugzeug	30 m	630 Pa	150 dB
Gewehrschuss	1 m	200 Pa	140 dB
Schmerzschwelle	am Ohr	100 Pa	134 dB
Gehörschäden bei kurzfristiger Einwirkung	am Ohr	ab 20 Pa	120 dB
Kampfflugzeug	100 m	6,3 - 200 Pa	110 - 140 dB
Presslufthammer, Diskothek	1 m / am Ohr	2 Pa	100 dB
Gehörschäden bei langfristiger Einwirkung	am Ohr	ab 0,63 Pa	85 dB
Hauptverkehrsstraße	10 m	0,2 - 0,63 Pa	80 - 90 dB
Pkw	10 m	0,02 - 0,2 Pa	60 - 80 dB
Fernseher auf Zimmerlautstärke	1 m	0,02 Pa	ca. 60 dB
Sprechender Mensch (normale Unterhaltung)	1 m	2 · 10-3 - 6,3 · 10-3 Pa	40 - 60 dB
Sehr ruhiges Zimmer	am Ohr	2 · 10-4 - 6,3 · 10-4 Pa	20 - 30 dB
Blätterrauschen, ruhiges Atmen	am Ohr	6,32 · 10-5 Pa	10 dB
Hörschwelle bei 2 kHz	am Ohr	2 · 10-5 Pa (20 µPa)	0 dB

Abhängigkeit von der Messentfernung

Bei Emissionsmessungen wird untersucht, welchen Schall eine bestimmte Schallquelle verursacht (z. B. Messung des Geräusches, das ein Flugzeug eines bestimmten Typs abstrahlt). Da der Schalldruckpegel immer von der Entfernung zur verursachenden Schallquelle abhängt, ist bei Emissionsmessungen neben der Angabe des gemessenen Pegels unbedingt auch die der Entfernung r erforderlich, in der die Messung durchgeführt wurde.

Bei Immissionsmessungen wird dagegen der Schalldruckpegel an dem Ort gemessen, an dem er auf den Menschen einwirkt. Ein Beispiel ist die Messung des Schalldruckpegels in einem Haus, das sich in der Einflugschneise eines Flughafens befindet. Bei Immissionsmessungen ist die Anzahl der vorhandenen Schallquellen sowie deren Abstand vom Messpunkt unerheblich.

Als Alternative wird bei Emissionsmessungen an der Störquelle oft der Schallleistungspegel angegeben, der entfernungs- und raumunabhängig ist, da er die gesamte, in alle Richtungen abgestrahlte Schallleistung der betreffenden Quelle ausdrückt. Der Schalldruckpegel, der in einer bestimmten Entfernung von der schallemittierenden Störquelle erzeugt wird, kann aus dem Schallleistungspegel direkt berechnet werden. In dieser Rechnung müssen allerdings die örtlichen Gegebenheiten der Szene, für die die Berechnung gelten soll, berücksichtigt werden.

Bei punktförmigen Schallquellen (sowie im Allgemeinen bei in alle Raumrichtungen gleichmäßig abstrahlenden Quellen) nimmt der Schalldruckpegel um ziemlich exakt 6 dB pro Abstandsverdopplung ab, also auf den Wert des halben Schalldrucks. Dieses ergibt sich aus der Tatsache, dass sich der Schalldruck umgekehrt proportional zum Abstand r von der Schallquelle nach dem sogenannten Abstandsgesetz (1/r-Gesetz) verhält. Rechnerisch lässt sich dieser Zusammenhang leicht aus der Berechnungsformel des Schalldrucks nachvollziehen:

$\Delta L = L_2 - L_1 = 10\,\cdot\,{\rm log}_{10} {\left(\frac{p_2}{p_0}\right)}^2 -\,10\,\cdot\,{\rm log}_{10} {\left(\frac{p_1}{p_0}\right)}^2 = 10\,\cdot\,{\rm log}_{10} {\left(\frac{p_2}{p_0}\frac{p_0}{p_1}\right)}^2 = 10\,\cdot\,{\rm log}_{10} {\left(\frac{p_2}{p_1}\right)}^2\,{\rm dB}$

Wenn also gemäß 1/r-Gesetz gilt: p₂/p₁ = r₁/r₂, so gilt für eine Verdopplung des Abstands (d. h. r₂ = 2· r₁):

$\Delta L = 10\,\cdot\,{\rm log}_{10} {\left(\frac{1}{2}\right)}^2\,{\rm dB} = 20\,\cdot\,{\rm log}_{10} {\left(\frac{1}{2}\right)}\, {\rm dB} = -20\,\cdot\,{\rm log}_{10} {\left(2\right)}\,{\rm dB} = -6{,}021\,{\rm dB} \approx -6\,{\rm dB}$

Gelegentlich wird behauptet, dass der Schalldruck mit 1/r² abnehme. Dieses gilt jedoch nur für quadratische Größen, wie Schallintensität oder Schallenergie. Auch hier ergibt sich bei Abstandsverdopplung aber eine Pegeldifferenz von 6 dB, da diese energetischen Größen, im Gegensatz zum Schalldruck, in der Berechnungsformel ihres Pegels nicht nochmals quadriert werden.

Addition der Schalldruckpegel mehrerer Schallquellen

Inkohärente Schallquellen

Bei der Addition inkohärenter Schallquellen ergibt sich der korrekte Summenpegel durch energetische Addition der beteiligten Schallquellen. Pegelwerte in Dezibel können nicht einfach addiert werden. Liegen von den zu addierenden Einzelschallquellen lediglich die Schalldruckpegel vor, so müssen daraus zunächst die quadrierten Schalldrücke (die zur Energie proportional sind) berechnet werden. Diesen Prozess nennt man "Entlogarithmieren" (in Analogie zum "Logarithmieren" bei der Berechnung eines Pegels).

Für den Summenschalldruckpegel von n inkohärent abstrahlenden Quellen gilt folglich:

$L_\Sigma = 10\,\cdot\,{\rm log}_{10} \left(\frac{p_1^2 + p_2^2 + \cdots + p_n^2}{p_0^2}\right) = 10\,\cdot\,{\rm log}_{10} \left(\left({\frac{p_1}{p_0}}\right)^2 + \left({\frac{p_2}{p_0}}\right)^2 + \cdots + \left({\frac{p_n}{p_0}}\right)^2\right)$

Aus der Berechnungsformel des Schalldruckpegels ergibt sich unmittelbar, dass gilt:

$\left({\frac{p_i}{p_0}}\right)^2 = 10^{\frac{L_i}{10}},\qquad i=1,2,\cdots,n$

Dieses in die Gleichung zur Berechnung des Summenschallpegels eingesetzt, ergibt die gesuchte Additionsformel:

$L_\Sigma = 10\,\cdot\,{\rm log}_{10} \left(10^{\frac{L_1}{10}} + 10^{\frac{L_2}{10}} + \cdots + 10^{\frac{L_n}{10}} \right)\,{\rm dB}$

Sonderfall gleich starker inkohärenter Schallquellen

An einem bestimmten Ort gleich starke Schallquellen erzeugen dort den gleichen Schalldruck, d h. auch den gleichen Schalldruckpegel. Bei der Addition solcher, inkohärenter, Quellen vereinfacht sich die obige Gleichung zur Berechnung des Summenschalldruckpegels wie folgt:

$\begin{align} L_\Sigma &= 10\,\cdot\,{\rm log}_{10} \left(10^{\frac{L_1}{10}} + 10^{\frac{L_2}{10}} + \cdots + 10^{\frac{L_n}{10}} \right)\,{\rm dB},\qquad L_1 = L_2 = \cdots = L_n \\ &= 10\,\cdot\,{\rm log}_{10} \left(n \cdot 10^{\frac{L_n}{10}}\right)\,{\rm dB}\\ &= 10\,\cdot \left({\rm log}_{10}(n) + {\rm log}_{10} \left(10^{\frac{L_n}{10}}\right)\right)\,{\rm dB}\\ &= 10\,\cdot\,{\rm log}_{10}(n)\,\,{\rm dB} + L_n \end{align}$

Für n = 2 gleich starke, inkohärente Schallquellen ergibt sich also z. B. ein Pegelzuwachs von 10 · log₁₀(2) dB = 3,01 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist.

Kohärente Schallquellen

Die Addition der Schalldruckpegel kohärenter Schallquellen kann nicht durch einfache energetische Addition vollzogen werden. Vielmehr tritt zwischen den Schallsignalen der verschiedenen Quellen Interferenz auf. Die Berechnung des Schalldruckpegels an einem bestimmten Ort ist durch Anwendung des Superpositionsprinzips möglich:

Je nachdem, wie die Phasenunterschiede der verschiedenen Schalle an dem betrachteten Punkt sind, tritt eine Verstärkung oder aber eine Abschwächung des Summenschalls auf. Maximale Verstärkung z. B. tritt dann auf, wenn der zurückgelegte Wegunterschied der verschiedenen Schalle gerade ein ganzes Vielfaches der Wellenlänge beträgt. Im Falle gleich starker, kohärenter Schallquellen erhöht sich der Pegel an diesen Punkten maximaler Verstärkung durch eine Verdoppelung der Quellenzahl um 6 dB.

An Punkten, deren Entfernung zu beiden Quellen sich um eine halbe Wellenlänge oder ein ungeradzahliges Vielfaches davon unterscheidet, löscht sich der Schall zum Teil aus. Im Sonderfall der gleich starken Quellen ist die Auslöschung vollständig, d. h. der Pegel geht gegen 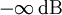$-\infty\, \mathrm{dB}$. An allen anderen Punkten im Raum nimmt der Pegel Werte an, die zwischen dem Maximum und dem Minimum liegen.

Für punktförmige Schallquellen im Freifeld ist eine analytische Berechnung des Pegels in Abhängigkeit vom Messort einfach durchzuführen. In geschlossenen Räumen stellt sich dagegen durch die Reflexionen ein komplexes Schallfeld ein, das nur numerisch unter Annahme von Vereinfachungen berechnet werden kann.

Ein Verfahren zur aktiven Geräuschminderung ist die Erzeugung von sogenanntem Antischall. Dabei wird der Interferenzeffekt, der zwischen kohärenten Schallsignalen auftritt, Gewinn bringend ausgenutzt: Ein Schallsignal mit dem gleichen Zeitverlauf sowie dem gleichen Betragsspektrum wie der Störschall, jedoch mit einem gegenüber dem Störschall um 180° verschobenen Phasenspektrum, löscht diesen gerade aus. Um solch gegenphasige Schalle an jedem Raumpunkt zu erzeugen, müsste man das gleiche Signal auf zwei am exakt gleichen Ort befindliche Lautsprecher geben und dabei einen der beiden Lautsprecher verpolen. Es würde dann überhaupt kein Schall abgestrahlt. Da sich in der Praxis niemals verschiedene Schallquellen an dem exakt gleichen Ort befinden können, ist es lediglich möglich, Schall so abzustrahlen, dass er sich an einem bestimmten Punkt als Antischall darstellt. Bei Entfernung des Hörers von diesem Punkt funktioniert die Auslöschung dann schlechter oder gar nicht, weil sich die Laufzeitdifferenzen zwischen Stör- und Antischall und dadurch die Phasenverschiebungen ändern. Zudem besteht in der Praxis ein Problem mit hohen Frequenzen: Aufgrund ihrer kurzen Wellenlänge können bereits minimale Abweichungen der Laufzeitdifferenzen zu signifikanten Phasenverschiebungen führen. Insofern stellen hier Ungenauigkeiten in den geometrischen Positionen (Schallquelle, Antischallquelle, Hörer), Verarbeitungszeiten des verwendeten Signalprozessors, sowie Temperaturschwankungen der Luft ein Problem dar.

Siehe auch

Quellen

1. ↑ D. W. Robinson und L. S. Whittle, Acustica, Vol. 10 (1960), S. 74–80
2. ↑ Zwicker E. und R. Feldtkeller: Das Ohr als Nachrichtenempfänger. S. Hirzel Verlag, Stuttgart, 1967

Weblinks

• Umrechnung: Schalldruck in Schalldruckpegel
• Das Ohmsche Gesetz der Akustik - Umrechnung
• Zusammenhang der akustischen Größen - pdf
• Addition von akustischen Schallpegeln