Schauderscher Fixpunktsatz

Der Fixpunktsatz von Schauder (nach Juliusz Schauder) gibt eine hinreichende Bedingung an, unter der eine Abbildung einen Fixpunkt besitzt. Er stellt eine starke Verallgemeinerung des Fixpunktsatzes von Brouwer dar, der stetige Funktionen auf konvexen, kompakten Teilmengen endlichdimensionaler Vektorräume behandelt.

Formulierung des Satzes

Der schaudersche Fixpunktsatz existiert in mehreren Versionen. Mit die allgemeinste Formulierung ist folgende:

Sei E ein hausdorffscher, topologischer Vektorraum und C eine nichtleere, kompakte und konvexe Teilmenge von E. Dann besitzt jede stetige Abbildung 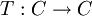$T:C\to C$ einen Fixpunkt.

Alternativen

Eine Alternative für Banachräume ist der banachsche Fixpunktsatz, da er neben der Existenz auch die Eindeutigkeit und diverse Fehlerabschätzungen behandelt. Er benötigt eine kontraktive Selbstabbildung, stellt dafür aber weniger starke Voraussetzungen an den Raum, in dem die Funktion definiert ist.

Beweis

Für den Fall, dass E ein lokalkonvexer Raum ist, wurde der Satz bereits sehr früh durch Tichonow bewiesen, während Schauder selbst nur einen fehlerhaften Beweis hatte. Der vollständige Beweis des Satzes wurde erst 2001 durch Robert Cauty erbracht. Selbst im lokalkonvexen Fall ist der Beweis aber noch um einiges komplizierter als beispielsweise der des banachschen Fixpunktsatzes. So wird in den bekannten Beweisen wesentlich der brouwersche Fixpunktsatz verwendet, dessen Beweis durchaus nichttrivial ist.

Referenzen

• Robert Cauty: Solution du problème de point fixe de Schauder. Fundamenta Mathematicae 170 (2001), Seiten 231-246.

Weblinks

• Beweis der Fixpunktsätze von Brouwer und Schauder (letzteren im Fall von Banachräumen)