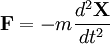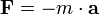Scheinkraft

Trägheitskräfte treten in beschleunigten Bezugssystemen auf, d. h. in solchen, bei denen es sich nicht um Inertialsysteme handelt.

Sie werden auch als Scheinkräfte bezeichnet, obwohl sie messbar sind und reale Wirkungen hervorrufen. Diese Bezeichnung rührt daher, dass sie nur in beschleunigten Koordinatensystemen auftreten und von einem Inertialsystem betrachtet nicht existieren.

Gleichmäßig beschleunigter Beobachter

Ein beschleunigter Beobachter, etwa der Insasse eines beschleunigenden oder bremsenden Autos oder der Fahrgast eines beschleunigenden oder bremsenden Eisenbahnzuges, spürt eine Trägheitskraft, die der Beschleunigung entgegengerichtet ist und proportional zur Masse des Beobachters und zur Beschleunigung ist.

In einem Auto, das nach vorne beschleunigt, ist die Trägheitskraft also nach hinten gerichtet. Die Insassen fühlen sich nach hinten in die Sitze gedrückt. Bei einem abbremsenden Auto ist die Beschleunigung negativ und die Trägheitskraft wirkt daher nach vorne. Im Falle eines Frontalaufpralls ist der Betrag der Beschleunigung und damit die nach vorne gerichtete Trägheitskraft so hoch, dass sie durch eine von einem Sicherheitsgurt oder durch einen Airbag ausgeübte Zwangskraft kompensiert werden muss, um zu verhindern, dass der Insasse nach vorne beschleunigt wird und gegen die Windschutzscheibe prallt.

Für einen stehenden Fahrgast in einer S-Bahn, die mit 1,0 m/s² beschleunigt, addiert sich zu der nach unten gerichteten Schwerkraft die nach hinten gerichtete Trägheitskraft, so dass er das Gefühl hat, sich auf einer schiefen Ebene zu befinden, die mit ca. 10 % Steigung 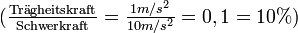$(\tfrac{\mathrm{Tr \ddot agheitskraft}}{\mathrm{Schwerkraft}} = \tfrac{1 m/s^2}{10 m/s^2} = 0,1 = 10%)$ nach vorne ansteigt. Um nicht umzukippen, muss er sich festhalten oder sein Gewicht verlagern. Erreicht die S-Bahn ihre Reisegeschwindigkeit, entfällt die Trägheitskraft und auch der Boden scheint wieder eben zu werden. Der Fahrgast muss dies wiederum ausgleichen, um nicht aus dem Gleichgewicht zu kommen.

Massenkraft

Trägheitskräfte spielen im Motorenbau eine wichtige Rolle und werden dort als Massenkräfte bezeichnet.

Rotierender Beobachter

Auf einen Beobachter, der sich in einem sich drehenden Bezugssystem befindet, wirkt eine Kraft, die senkrecht auf der Drehachse steht und von dieser weg gerichtet ist. Ihr Betrag ist proportional zur Masse des Beobachters, zum Quadrat der Drehfrequenz und zum Abstand von der Drehachse. Diese Kraft nennt man Fliehkraft bzw. Zentrifugalkraft.

Falls sich der Beobachter im rotierenden Bezugssystem bewegt, wirkt auf ihn neben der Zentrifugalkraft auch die Corioliskraft. Diese steht senkrecht auf der Bewegungsrichtung und auf der Drehachse und ist proportional zur Masse des Beobachters, zur Drehfrequenz, zur Geschwindigkeit des Beobachters und zum Sinus des Winkels zwischen der Bewegungsrichtung und der Drehachse.

Formeln

Wir betrachten ein Objekt mit Masse m in einem Inertialsystem A. Die Position des beschleunigten Bezugssystems B im Inertialsystem A sei X(t). Fettdruck bezeichnet hier und im Folgenden Vektoren.

Dann ist die Trägheitskraft

$\bold{F} = - m \frac{d^2\bold{X}}{dt^2}$

Bei gleichmäßiger Beschleunigung a wird dies zu

$\mathbf{F} = -m \cdot \mathbf{a}$

Im rotierenden Bezugssystem ist die Trägheitskraft

$\mathbf{F} = - 2 m \boldsymbol\omega \times \mathbf{v} - m \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf{r} ) - m \frac{d \boldsymbol\omega }{dt} \times \mathbf{r}$ ,

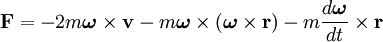wobei 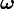$\boldsymbol\omega$ die Winkelgeschwindigkeit, v die Geschwindigkeit des Objektes im rotierenden Koordinatensystem und r der Ort des Objektes ist.

Der erste Term auf der rechten Seite ist die Corioliskraft, der zweite Term ist die Fliehkraft und der dritte Term ist die Euler-Kraft.

Schwerkraft als Trägheitskraft

Im Rahmen der allgemeinen Relativitätstheorie sind frei fallende Bezugsysteme lokal äquivalent zu Inertialsystemen. Daher kann auch die Schwerkraft als Trägheitskraft angesehen werden, die daraus resultiert, dass ein Beobachter auf der Erdoberfläche konstant gegen ein frei fallendes Bezugsystem beschleunigt wird. Die genannte Äquivalenz gilt jedoch nur lokal, da im frei fallenden Bezugssystem in einem Gravitationsfeld Gezeitenkräfte auftreten. Nach der allgemeinen Relativitätstheorie ist also die Schwerkraft für ausgedehnte Körper wegen der nur lokal definierbaren Inertialsysteme nicht als klassische Trägheitskraft zu verstehen.

Die allgemeine Relativitätstheorie erweitert jedoch das Relativitätsprinzip, indem sie fordert, dass die Naturgesetze in allen möglichen Koordinatensystemen dieselbe Form annehmen. Die Beschränkung auf Inertialsysteme ist dabei nur noch näherungsweise lokal möglich, da diese nur näherungsweise lokal existieren. In dieser forminvarianten, kovarianten Formulierung entstehen Trägheitskräfte nicht dadurch, dass sich Beobachter nicht-inertial bewegen, sondern dadurch, dass sie sich nicht auf Geodäten der Raumzeit bewegen. In diesem Sinne ist auch die Schwerkraft als Trägheitskraft zu verstehen, da auch Gezeitenkräfte nur dadurch auftreten, dass die Steifigkeit eines ausgedehnten Körpers einige Punkte des Körpers von einer geodätischen Bewegung weg beschleunigt.