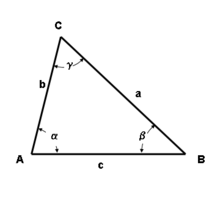
- Schiefwinkliges Dreieck
-
Ein schiefwinkliges Dreieck ist ein Dreieck, das keinen rechten Winkel besitzt. Man kann es in spitzwinklige und stumpfwinklige Dreiecke unterteilen.
Inhaltsverzeichnis
Sinussatz
Der Sinussatz stellt ein Verhältnis zwischen den Seiten und Winkeln eines allgemeinen Dreiecks her. Außerdem lässt sich mit ihm der Umkreisradius R des Dreiecks berechnen:
Kosinussatz
Der Kosinussatz ist eine Verallgemeinerung des Satzes des Pythagoras. Er stellt die drei Seiten und einen Winkel eines allgemeinen Dreiecks miteinander in Beziehung:
Der Kosinussatz ist zyklisch vertauschbar; es gilt also Analoges für die anderen Seiten.
Grundaufgaben
Je nach gegebenen Bestimmungsstücken unterscheidet man drei Grundaufgaben beim Dreieck:
- Eine Seite, zwei Winkel
- Zwei Seiten, ein Winkel
- Drei Seiten
Grundaufgabe 1: Eine Seite, zwei Winkel
Hierbei unterscheidet man zwei Fälle: Den WSW- und den SWW-Fall. In beiden Fällen lässt sich der dritte Winkel über die Winkelsumme bestimmen. Die Seiten lassen sich über den Sinussatz berechnen.
Grundaufgabe 2: Zwei Seiten, ein Winkel
Auch hier können zwei Fälle auftreten. Der SSW-Fall ist nicht eindeutig, wenn die dem Winkel gegenüber liegende Seite kleiner ist als die gegebene anliegende Seite. Der zweite Winkel lässt sich über den Sinussatz berechnen. Dabei ist zu beachten, dass der neue Winkel stumpf sein kann, wenn die dem gegebenen Winkel gegenüber liegende Seite die kürzere ist. Der dritte Winkel lässt sich über die Winkelsumme bestimmen. Für die dritte Seite kann man abermals den Sinussatz verwenden.
Beim SWS-Fall verwendet man den Kosinussatz für die dritte Seite. Die beiden übrigen Winkel lassen sich über den Sinussatz berechnen.
Grundaufgabe 3: Drei Seiten
Beim SSS-Fall bestimmt man zuerst einen Winkel über den Kosinussatz. Anschließend lassen sich die restlichen Winkel durch den Sinussatz bestimmen.
Literatur
- Walter Strampp: Elementare Mathematik: Vor- und Aufbaukurs. Oldenbourg 2002, ISBN 3486259563, S. 124 (eingeschränkte Online-Version (Google Books))
- Zeidler, Schwarz, Hackbusch et.al.: Teubner-Taschenbuch der Mathematik . B.G.Teubner Stuttgart, Leipzip 1996, S. 758ff (eingeschränkte Online-Version (Google Books))
Weblinks
Wikimedia Foundation.