- Schlichte Abbildung
-
In der Funktionentheorie ist eine biholomorphe Abbildung eine bijektive holomorphe Abbildung mit holomorpher Umkehrabbildung.
Inhaltsverzeichnis
Eigenschaften
- Eine bijektive holomorphe Abbildung ist immer biholomorph. Im eindimensionalen Fall folgt dies direkt aus dem Satz über implizite Funktionen, in höheren Dimensionen aus dem Satz von Osgood.
- Im eindimensionalen Fall ist eine biholomorphe Abbildung eine konforme Abbildung. Umgekehrt ist eine bijektive, stetig differenzierbare Abbildung von Gebieten der komplexen Ebene, die konform und orientierungserhaltend ist und deren Ableitung nicht verschwindet, ebenfalls biholomorph.
Eindimensionale Beispiele
Die lineare Funktion
- w = f(z) = az + b (mit a, b, w, z als komplexen Zahlen der Form z = x + iy) ergibt
- für a = 1 und b nicht gleich Null eine Verschiebung (Translation)
- für
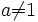 reell und positiv eine zentrische Streckung mit dem Streckfaktor a und Streckzentrum
reell und positiv eine zentrische Streckung mit dem Streckfaktor a und Streckzentrum 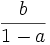 ;
; - für | a | = 1 und b = 0 eine Drehung. Verwendet man nämlich Polarkoordinaten für die Zahl z, so kann der "Punkt"z durch (rz,φz) gekennzeichnet werden (s. Abb. 1). Weil
-
- z = rz (cos φ + i sin φ)
ist, erhält man mit der Eulerformel
-
- eiφ = cos φ + i sin φ
- w = az = raeiφa. rzeiφz.
Wenn |a|=1 gesetzt wird, ist ra = 1 und somit
-
-
- w = rz ei(φa+φz).
-
Der Punkt Z (mit dem Argument (Bogenmaß) φz und dem Betrag r = rz) geht somit in den Punkt W (mit φa+φz) und dem Betrag rz über, das ist eine Drehung.
- für |a| ungleich 1 und b = 0 eine Drehstreckung.
Beispielsweise führt die Drehstreckung w = (1+i)z den Punkt z = 2+3i in den Bildpunkt w = (1+i)(2+3i) = -1+5i über. Die Bildpunkte zweier weiterer Punkte, die mit dem ersten ein Dreieck bilden können, lassen sich ebenso berechnen, so daß das Bilddreieck gezeichnet werden kann und damit diese Drehstreckung sich leicht veranschaulichen lässt.
- für |a| nicht gleich 1, und b nicht gleich 0 eine Drehstreckung mit Verschiebung.
Inversion
Die Abbildung
- w = f(z) = 1/z
heißt Inversion. Bei ihr wird das Innere des Kreises mit Radius = 1 (sog. Einheitskreis) auf das Äußere, das Äußere in das Innere abgebildet, der Rand des Kreises geht in sich selber über, 1 und -1 werden auf 1 und -1 abgebildet, das sind die beiden Fixpunkte der Inversion.
Quadratfunktion
Bei der Quadratfunktion
- w = f(z) = z2
ist f' nicht Null, wenn z nicht Null ist. Wählt man Definitions- und Zielbereich so, dass die Null nicht enthalten ist und die Einschränkung von f bijektiv ist, erhält man folglich eine biholomorphe Abbildung. Man kann beispielsweise
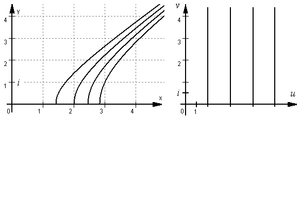
wählen, also als Definitionsbereich die rechte Halbebene und als Zielbereich die entlang der negativen reellen Achse geschlitzte Ebene.
Aus w = u + iv = (x + iy)2 = x2 - y2 + (2xy)i ergibt der Vergleich der Koeffizienten bei Real- und Imaginärteil
- u = x2 - y2 und v = 2xy.
Die zur x-Achse symmetrisch liegenden Hyperbeln (vgl. Abb. 2)
x2 - y2 = const gehen in vertikale Parallelen u = const über. Die zur ersten Winkelhalbierenden symmetrisch liegenden Hyperbeln 2xy = const gehen in waagrecht verlaufende Parallelen über.
Wikimedia Foundation.