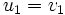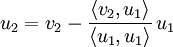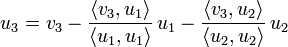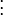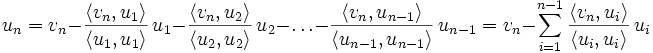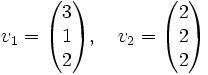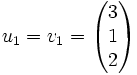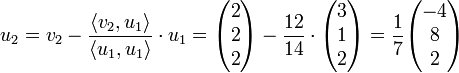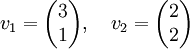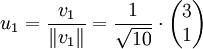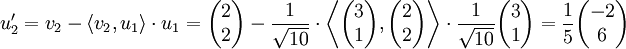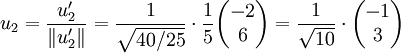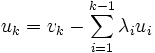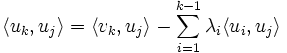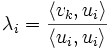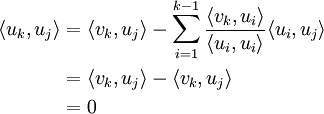- Schmidtsches Orthonormalisierungsverfahren
-
Das Gram-Schmidtsche Orthogonalisierungsverfahren ist ein Algorithmus aus dem mathematischen Teilgebiet der linearen Algebra. Er erzeugt zu jedem System linear unabhängiger Vektoren aus einem Prähilbertraum, d. h. einem Vektorraum mit Skalarprodukt, ein Orthogonalsystem, das denselben Untervektorraum erzeugt. Eine Erweiterung stellt das Gram-Schmidtsche Orthonormalisierungsverfahren dar: statt eines Orthogonalsystems berechnet es ein Orthonormalsystem. Verwendet man ein System von Basisvektoren des Prähilbertraums als Eingabe für die Algorithmen, so berechnen sie eine Orthogonal- bzw. Orthonormalbasis.
Die beiden Verfahren sind nach Jørgen Pedersen Gram und Erhard Schmidt benannt. Sie wurden allerdings bereits früher in den Werken von Pierre-Simon Laplace und Augustin Louis Cauchy verwendet.
Für die numerische Berechnung durch einen Computer sind die Gram-Schmidt-Verfahren nicht geeignet. Durch akkumulierte Rundungsfehler sind die berechneten Vektoren nicht mehr orthogonal. Es existieren aber Modifikationen des Verfahrens, die diesen Fehler nicht haben. Weitere Möglichkeiten für Orthogonalisierungsverfahren basieren auf Householdertransformationen oder Givens-Rotationen.
Inhaltsverzeichnis
Algorithmus des Orthogonalisierungsverfahrens
Der folgende Algorithmus berechnet zu den linear unabhängigen Vektoren
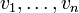 ein Orthogonalsystem von n paarweise orthogonalen Vektoren, das denselben Untervektorraum erzeugt.
ein Orthogonalsystem von n paarweise orthogonalen Vektoren, das denselben Untervektorraum erzeugt.Die einzelnen Vektoren
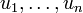 des Orthogonalsystems berechnen sich wie folgt:
des Orthogonalsystems berechnen sich wie folgt:Beispiel
Im
 versehen mit dem Standardskalarprodukt
versehen mit dem Standardskalarprodukt 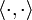 seien zwei linear unabhängige Vektoren vorgegeben, die einen Untervektorraum erzeugen:
seien zwei linear unabhängige Vektoren vorgegeben, die einen Untervektorraum erzeugen:Es werden nun zwei orthogonale Vektoren u1 und u2 berechnet, die denselben Untervektorraum erzeugen:
Algorithmus des Orthonormalisierungsverfahrens
Der folgende Algorithmus berechnet zu den linear unabhängigen Vektoren
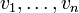 ein Orthonormalsystem von n normierten, paarweise orthogonalen Vektoren, das denselben Untervektorraum erzeugt.
ein Orthonormalsystem von n normierten, paarweise orthogonalen Vektoren, das denselben Untervektorraum erzeugt.Die einzelnen Vektoren
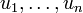 des Orthonormalsystems erhält man, indem zuerst jeweils ein orthogonaler Vektor berechnet und anschließend normalisiert wird:
des Orthonormalsystems erhält man, indem zuerst jeweils ein orthogonaler Vektor berechnet und anschließend normalisiert wird: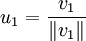 (Normalisieren des ersten Vektors v1)
(Normalisieren des ersten Vektors v1)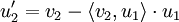 (Orthogonalisieren des zweiten Vektors v2)
(Orthogonalisieren des zweiten Vektors v2)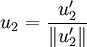 (Normalisieren des Vektors
(Normalisieren des Vektors 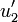 )
)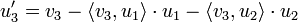 (Orthogonalisieren des dritten Vektors v3)
(Orthogonalisieren des dritten Vektors v3)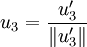 (Normalisieren des Vektors
(Normalisieren des Vektors 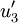 )
)
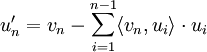 (Orthogonalisieren des n-ten Vektors vn)
(Orthogonalisieren des n-ten Vektors vn)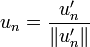 (Normalisieren des Vektors
(Normalisieren des Vektors 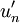 )
)
Im Allgemeinen erhält man durch dieses Verfahren kein besonders ausgezeichnetes System. Im
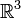 muss z.B. erst ein Umordnungsschritt nachgeschaltet werden, um ein Rechts- oder Linkssystem zu erhalten.
muss z.B. erst ein Umordnungsschritt nachgeschaltet werden, um ein Rechts- oder Linkssystem zu erhalten.Beispiel
Im
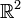 versehen mit dem Standardskalarprodukt
versehen mit dem Standardskalarprodukt 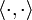 seien zwei Basisvektoren gegeben:
seien zwei Basisvektoren gegeben:Es werden nun zwei Vektoren u1 und u2 berechnet, die eine Orthonormalbasis des
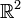 bilden.
bilden.Anmerkungen
Eine besondere Eigenschaft der beiden Verfahren ist, dass nach jedem Zwischenschritt die bisher berechneten Vektoren
 den gleichen Vektorraum erzeugen wie die Vektoren
den gleichen Vektorraum erzeugen wie die Vektoren  . Die Vektoren
. Die Vektoren  bilden also eine Orthogonal- bzw. Orthonormalbasis der entsprechenden Untervektorräume. Anders ausgedrückt ist die Transformationsmatrix, die die Koordinaten des einen Systems im anderen ausdrückt, eine rechtsobere Dreiecksmatrix. Fasst man die orthonormalen Vektoren
bilden also eine Orthogonal- bzw. Orthonormalbasis der entsprechenden Untervektorräume. Anders ausgedrückt ist die Transformationsmatrix, die die Koordinaten des einen Systems im anderen ausdrückt, eine rechtsobere Dreiecksmatrix. Fasst man die orthonormalen Vektoren 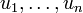 als Spalten einer Matrix Q zusammen, ebenso die Vektoren des Ausgangssystems
als Spalten einer Matrix Q zusammen, ebenso die Vektoren des Ausgangssystems 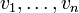 zu einer Matrix A, so gibt es eine Dreiecksmatrix R mit A=QR, es wird also eine QR-Zerlegung bestimmt. Dementsprechend kann das Ergebnis der Gram-Schmidt-Orthonormalisierung auch mit anderen Methoden zur QR-Zerlegung bestimmt werden, die mit Givens-Rotationen oder Householder-Spiegelungen arbeiten.
zu einer Matrix A, so gibt es eine Dreiecksmatrix R mit A=QR, es wird also eine QR-Zerlegung bestimmt. Dementsprechend kann das Ergebnis der Gram-Schmidt-Orthonormalisierung auch mit anderen Methoden zur QR-Zerlegung bestimmt werden, die mit Givens-Rotationen oder Householder-Spiegelungen arbeiten.Berechnet man ein Orthonormalsystem von Hand, ist es oftmals einfacher, zunächst ein Orthogonalsystem auszurechnen und dann die einzelnen Vektoren zu normieren. Dadurch erspart man sich das zweifache Normieren und kann oftmals mit einfacheren Werten rechnen. Gegebenenfalls lohnt es sich, vor dem Erstellen des Orthogonalsystems/Orthonormalsystems das Gaußsche Eliminationsverfahren durchzuführen.
Funktionsprinzip der Verfahren
Sind die orthogonalen Vektoren
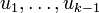 bereits bestimmt, versuchen wir, von vk eine passende Linearkombination der Vektoren
bereits bestimmt, versuchen wir, von vk eine passende Linearkombination der Vektoren 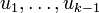 abzuziehen, so dass der Differenzvektor
abzuziehen, so dass der Differenzvektorzu allen Vektoren
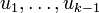 orthogonal wird, d.h. jedes der Skalarprodukte
orthogonal wird, d.h. jedes der Skalarproduktemit
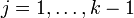 muss den Wert 0 ergeben. Hierfür ist die Wahl
muss den Wert 0 ergeben. Hierfür ist die Wahlpassend. Setzte man dieses λi ein, so erhält man
Literatur
- Andrzej Kielbasiński, Hubert Schwetlick: Numerische lineare Algebra. Eine computerorientierte Einführung. Deutscher Verlag der Wissenschaften, Berlin 1988, ISBN 3-326-00194-0.
Wikimedia Foundation.