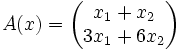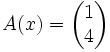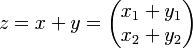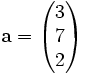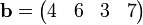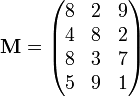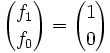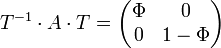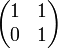- LinA
-
Die Lineare Algebra (auch Vektoralgebra) ist ein Teilgebiet der Mathematik, das sich mit Vektorräumen und linearen Abbildungen zwischen diesen beschäftigt. Dies schließt insbesondere auch die Betrachtung von linearen Gleichungssystemen und Matrizen mit ein.
Vektorräume und deren lineare Abbildungen sind ein wichtiges Hilfsmittel in vielen Bereichen der Mathematik. Außerhalb der reinen Mathematik finden sich Anwendungen u. a. in den Naturwissenschaften und in der Wirtschaftswissenschaft (z. B. in der Optimierung).
Die lineare Algebra entstand aus zwei konkreten Anforderungen heraus: einerseits dem Lösen von linearen Gleichungssystemen, andererseits der rechnerischen Beschreibung geometrischer Objekte, der so genannten analytischen Geometrie (daher bezeichnen manche Autoren Lineare Algebra als Lineare Geometrie).
Inhaltsverzeichnis
Geschichte
Im Jahr 1750 veröffentlichte Gabriel Cramer die nach ihm benannte Cramer’sche Regel. Damit war man erstmals im Besitz einer Lösungsformel für viele lineare Gleichungssysteme. Die Cramer’sche Regel gab zudem entscheidende Impulse für die Entwicklung der Determinantentheorie in den folgenden fünfzig Jahren.
Die Geschichte der modernen linearen Algebra reicht zurück bis in die Jahre 1843 und 1844. 1843 erdachte William Rowan Hamilton (von dem der Begriff Vektor stammt) mit den Quaternionen eine Erweiterung der komplexen Zahlen. 1844 veröffentlichte Hermann Grassmann sein Buch Die lineare Ausdehnungslehre. Arthur Cayley führte dann 1857 mit den 2×2-Matrizen eine der grundlegendsten algebraischen Ideen ein.
Lineare Gleichungssysteme
Als lineare Gleichungssysteme bezeichnet man eine Zusammenfassung von Gleichungen der Art
- x1 + x2 = 1
- 3x1 + 6x2 = 4
Derartige Gleichungssysteme erhält man aus vielen alltäglichen Fragestellungen, beispielsweise:
- In welchem Verhältnis muss man eine 30%-ige Lösung und eine 60%-ige Lösung mischen, um eine 40%-ige Lösung zu erhalten?
Der wesentliche Abstraktionsschritt der linearen Algebra besteht nun darin, die linken Seiten als eine Funktion A der Unbekannten x = (x1,x2) aufzufassen:
Dann wird die Lösung des Gleichungssystems zu der Aufgabe: Finde ein x, so dass
gilt. Das Übereinanderschreiben ist dabei lediglich ein Formalismus, um mit mehr als einer Zahl gleichzeitig umgehen zu können.
Statt A schreibt man auch einfach die relevanten Zahlen in Form eines Rechtecks auf und nennt das Objekt eine Matrix:
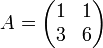 .
.
Man stellt fest, dass die Funktion A spezielle Eigenschaften hat, sie ist eine lineare Abbildung. Ist x eine Lösung für das Gleichungssystem A(x) = b, und y eine Lösung des Gleichungssystems A(y) = c, so ist
eine Lösung von A(z) = b + c. Man kann das auch in der Form A(x + y) = A(x) + A(y) schreiben. Ist weiter λ irgendeine reelle Zahl, so ist
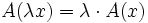 ; dabei ist
; dabei ist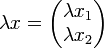 .
.
Siehe auch: Lineares Gleichungssystem
Analytische Geometrie
Der andere Ursprung der linearen Algebra findet sich in der rechnerischen Beschreibung des 2- und 3-dimensionalen (euklidischen) Raumes, auch „Anschauungsraum“ genannt. Mit Hilfe eines Koordinatensystems können Punkte im Raum durch Tripel (x1,x2,x3) von Zahlen beschrieben werden. Der Abbildungtyp der Verschiebung führt zum Begriff des Vektors, der Richtung und Betrag der Verschiebung angibt. Viele physikalische Größen, beispielsweise Kräfte, haben stets diesen Richtungsaspekt.
Da man auch Vektoren durch Zahlentripel (a1,a2,a3) beschreiben kann, verschwimmt die Trennung zwischen Vektoren und Punkten: einem Punkt P entspricht sein Ortsvektor, der vom Koordinatenursprung nach P zeigt.
Viele der in der klassischen Geometrie betrachteten Abbildungstypen, beispielsweise Drehungen um Achsen durch den Ursprung oder Spiegelungen an Ebenen durch den Ursprung, gehören zur Klasse der linearen Abbildungen, die schon oben erwähnt wurde.
Siehe auch: Analytische Geometrie
Vektorräume und lineare Algebra
Der Begriff des Vektorraumes entsteht als Abstraktion der obigen Beispiele: Ein Vektorraum ist eine Menge, deren Elemente Vektoren genannt werden, zusammen mit
- einer Addition von Vektoren
- einer Multiplikation von Vektoren mit Elementen eines fixierten Körpers, Skalarmultiplikation (äußere Multiplikation) genannt.
Diese Addition und die Skalarmultiplikation müssen noch einige einfache Eigenschaften erfüllen, die auch für die Vektoren im Anschauungsraum gelten.
Man könnte sagen, dass Vektorräume gerade so definiert sind, dass man von linearen Abbildungen zwischen ihnen sprechen kann.
In gewisser Weise ist der Begriff des Vektorraums für die Lineare Algebra bereits zu allgemein. Man kann jedem Vektorraum eine Dimension zuordnen, beispielsweise hat die Ebene Dimension 2 und der Raum Dimension 3. Es gibt aber Vektorräume, deren Dimension nicht endlich ist, und viele der bekannten Eigenschaften gehen verloren. Es hat sich aber als sehr erfolgreich erwiesen, unendlichdimensionale Vektorräume mit einer zusätzlichen topologischen Struktur auszustatten; die Untersuchung topologischer Vektorräume ist Gegenstand der Funktionalanalysis.
Der Rest dieses Artikels beschäftigt sich mit dem Fall endlicher Dimensionen.
Wichtige Sätze und Ergebnisse
Jeder Vektorraum hat mindestens eine Basis. Je zwei Basen eines Vektorraumes haben gleich viele Elemente; nur deshalb ist es sinnvoll von der Dimension eines Vektorraumes zu sprechen. Für Summen und Durchschnitte von Untervektorräumen gilt die Dimensionsformel und für die Dimensionen von Faktorräumen die Formel
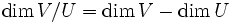 .
.Jede lineare Abbildung
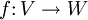 ist durch die Angabe der Bilder einer Basis von V eindeutig festgelegt. Für lineare Abbildungen gilt der Homomorphiesatz und der Rangsatz. Sie können bezüglich fest gewählter Basen durch Matrizen dargestellt werden. Dabei entspricht der Hintereinanderausführung von linearen Abbildungen die Multiplikation ihrer Darstellungsmatrizen.
ist durch die Angabe der Bilder einer Basis von V eindeutig festgelegt. Für lineare Abbildungen gilt der Homomorphiesatz und der Rangsatz. Sie können bezüglich fest gewählter Basen durch Matrizen dargestellt werden. Dabei entspricht der Hintereinanderausführung von linearen Abbildungen die Multiplikation ihrer Darstellungsmatrizen.Ein lineares Gleichungssystem
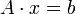 mit
mit 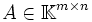 ,
, 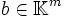 und
und 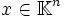 ist genau dann lösbar, wenn der Rang der Matrix A gleich dem Rang der erweiterten Koeffizientenmatrix
ist genau dann lösbar, wenn der Rang der Matrix A gleich dem Rang der erweiterten Koeffizientenmatrix 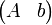 ist. In diesem Fall ist die Lösungsmenge des Systems ein affiner Unterraum von
ist. In diesem Fall ist die Lösungsmenge des Systems ein affiner Unterraum von 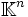 der Dimension n − rang(A). Für nicht zu große Gleichungssysteme kann die Rangbestimmung und die Berechnung des Lösungsraumes mit dem Gaußschen Eliminationsverfahren durchgeführt werden.
der Dimension n − rang(A). Für nicht zu große Gleichungssysteme kann die Rangbestimmung und die Berechnung des Lösungsraumes mit dem Gaußschen Eliminationsverfahren durchgeführt werden.Eine lineare Abbildung
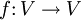 (also ein Endomorphismus) eines endlichdimensionalen Vektorraumes V ist bereits invertierbar, wenn sie injektiv oder surjektiv ist. Dies ist wiederum genau dann der Fall, wenn ihre Determinante ungleich null ist. Hieraus folgt, dass die Eigenwerte eines Endomorphismus genau die Nullstellen seines charakteristischen Polynoms sind. Eine weitere wichtige Aussage über das charakteristische Polynom ist der Satz von Cayley-Hamilton.
(also ein Endomorphismus) eines endlichdimensionalen Vektorraumes V ist bereits invertierbar, wenn sie injektiv oder surjektiv ist. Dies ist wiederum genau dann der Fall, wenn ihre Determinante ungleich null ist. Hieraus folgt, dass die Eigenwerte eines Endomorphismus genau die Nullstellen seines charakteristischen Polynoms sind. Eine weitere wichtige Aussage über das charakteristische Polynom ist der Satz von Cayley-Hamilton.Ein Endomorphismus (bzw. eine quadratische Matrix) ist genau dann diagonalisierbar, wenn das charakteristische Polynom in Linearfaktoren zerfällt und für jeden Eigenwert dessen algebraische Vielfachheit gleich der geometrischen Vielfachheit, also der Dimension des zugehörigen Eigenraumes ist. Äquivalent dazu ist die Existenz einer Basis des Vektoraumes, die aus Eigenvektoren der linearen Abbildung besteht. Endomorphismen, deren charakteristisches Polynom in Linearfaktoren zerfällt, sind immerhin noch trigonalisierbar, können also durch eine Dreiecksmatrix dargestellt werden. Ein etwas tiefer liegendes Ergebnis ist, dass die darstellende Matrix dabei sogar in jordansche Normalform gebracht werden kann.
In Vektorräumen, auf denen zusätzlich ein Skalarprodukt gegeben ist, wird durch
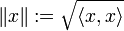 eine Norm definiert. In diesen Skalarprodukträumen existieren stets Orthonormalbasen, die etwa durch das Gram-Schmidtsche Orthonormalisierungsverfahren konstruiert werden können. Nach dem Projektionssatz kann man in diesen Räumen die Bestapproximation aus einem Untervektorraum durch orthogonale Projektion bestimmen.
eine Norm definiert. In diesen Skalarprodukträumen existieren stets Orthonormalbasen, die etwa durch das Gram-Schmidtsche Orthonormalisierungsverfahren konstruiert werden können. Nach dem Projektionssatz kann man in diesen Räumen die Bestapproximation aus einem Untervektorraum durch orthogonale Projektion bestimmen.Bezüglich der Diagonalisierbarkeit von Endomorphismen in Skalarprodukträumen stellt sich die Frage, ob eine Orthonormalbasis aus Eigenvektoren existiert. Das zentrale Resultat hierzu ist der Spektralsatz. Insbesondere gilt im reellen Fall: Zu jeder symmetrischen Matrix
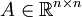 gibt es eine orthogonale Matrix Q, so dass QTAQ eine Diagonalmatrix ist. Wendet man dieses Ergebnis auf quadratische Formen an, ergibt sich der Satz von der Hauptachsentransformation.
gibt es eine orthogonale Matrix Q, so dass QTAQ eine Diagonalmatrix ist. Wendet man dieses Ergebnis auf quadratische Formen an, ergibt sich der Satz von der Hauptachsentransformation.Auch Bilinearformen und Sesquilinearformen können bei fest gewählten Basen durch Matrizen dargestellt werden. Eine Bilinearform ist genau dann symmetrisch und positiv definit, also ein Skalarprodukt, wenn ihre darstellende Matrix symmetrisch und positiv definit ist. Eine symmetrische Matrix ist genau dann positiv definit, wenn alle ihre Eigenwerte positiv sind. Allgemein gilt für symmetrische Bilinearformen und hermitesche Sesquilinearformen der Trägheitssatz von Sylvester, der besagt, dass die Anzahl der positiven und negativen Eigenwerte der darstellenden Matrizen nicht von der Wahl der Basis abhängen.
Vektoren und Matrizen
Vektoren können durch ihre Komponenten beschrieben werden, die (je nach Anwendung) als (hier 3-dimensionaler) Spaltenvektor
oder (hier 4-dimensionaler) Zeilenvektor
geschrieben werden.
In der Literatur werden Vektoren unterschiedlich von anderen Größen unterschieden: Es werden Kleinbuchstaben, fettgedruckte Kleinbuchstaben, unterstrichene Kleinbuchstaben oder Kleinbuchstaben mit einem Pfeil darüber benutzt. Dieser Artikel verwendet Kleinbuchstaben.
Eine Matrix wird durch ein 'Raster' von Zahlen angegeben. Hier ist eine Matrix mit 4 Zeilen und 3 Spalten:
Matrizen werden meistens mit Großbuchstaben bezeichnet.
Einzelne Elemente eines Vektors werden bei Spaltenvektoren in der Regel durch einen Index angegeben: Das 2. Element des oben angegebenen Vektors a wäre dann a2=7. In Zeilenvektoren wird manchmal eine Hochzahl verwendet, wobei man aufpassen muss, ob eine Vektorindizierung oder ein Exponent vorliegt: Mit dem obigen Beispiel b hat man etwa b4=7.
Matrixelemente werden durch zwei Indizes angegeben. Dabei werden die Elemente durch Kleinbuchstaben dargestellt: m2,3=2 ist das Element in der 3. Spalte der 2. Zeile.
Der verallgemeinerte Begriff dieser Gebilde ist Tensor, Skalare sind Tensoren 0. Stufe, Vektoren Tensoren 1. Stufe, Matrizen Tensoren 2. Stufe. Ein Tensor n. Stufe kann durch einen n-dimensionalen Zahlen-Würfel repräsentiert werden.
Matrizen spezieller Form
In der linearen Algebra ist es oft erforderlich, Matrizen mittels elementarer Zeilenumformungen oder Basiswechsel auf eine spezielle Form zu bringen. Wichtig sind dabei folgende Formen:
- Dreiecksmatrix,
- Diagonalmatrix und
- Matrizen in Jordanform.
Endomorphismen und quadratische Matrizen
Bei der Darstellung einer linearen Abbildung – wie unter Matrix beschrieben – gibt es den Sonderfall einer linearen Abbildung f eines endlich-dimensionalen Vektorraums auf sich selbst (eines sog. Endomorphismus). Man kann dann dieselbe Basis v für Urbild- und Bildkoordinaten verwenden und erhält eine quadratische Matrix A = vfv, so dass die Anwendung der linearen Abbildung der Linksmultiplikation mit A entspricht. Die zweimalige Hintereinanderausführung dieser Abbildung entspricht dann der Multiplikation mit A2 usw., und man kann alle polynomialen Ausdrücke mit A (Summen von Vielfachen von Potenzen von A) als lineare Abbildungen des Vektorraums auffassen.
Invertierbarkeit
Analog zur Rechenregel x0 = 1 bei Zahlen ist die nullte Potenz einer quadratischen Matrix die Diagonalmatrix E (Einheitsmatrix) mit Einsen auf der Diagonalen und in der alle restlichen Elemente Null sind, sie entspricht der Identitätsabbildung jedes Vektors auf sich selbst. Negative Potenzen einer quadratischen Matrix A lassen sich nur berechnen, wenn die durch A gegebene lineare Abbildung invertierbar ist, also keine zwei unterschiedlichen Vektoren u1 und u2 auf denselben Vektor Au1 = Au2 abbildet. Anders ausgedrückt, muss für eine invertierbare Matrix A aus
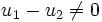 stets
stets 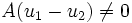 folgen, das lineare Gleichungssystem Au = 0 darf also nur die Lösung 0 haben. Zu einer invertierbaren Matrix A existiert eine inverse Matrix A − 1 mit A − 1A = AA − 1 = E.
folgen, das lineare Gleichungssystem Au = 0 darf also nur die Lösung 0 haben. Zu einer invertierbaren Matrix A existiert eine inverse Matrix A − 1 mit A − 1A = AA − 1 = E.Determinanten
Eine Determinante ist eine spezielle Funktion, die einer quadratischen Matrix eine Zahl zuordnet. Diese Zahl gibt Auskunft über einige Eigenschaften der Matrix. Beispielsweise lässt sich an ihr erkennen, ob eine Matrix invertierbar ist. Eine weitere wichtige Anwendung ist die Berechnung des charakteristischen Polynoms und damit der Eigenwerte der Matrix.
Es gibt geschlossene Formeln zur Berechnung der Determinanten, wie den Laplace’schen Entwicklungssatz oder die Leibniz-Formel. Diese Formeln sind jedoch eher von theoretischem Wert, da ihr Aufwand bei größeren Matrizen stark ansteigt. In der Praxis kann man Determinanten am leichtesten berechnen, indem man die Matrix mit Hilfe des Gauß-Algorithmus in obere oder untere Dreiecksform bringt, die Determinante ist dann einfach das Produkt der Hauptdiagonalelemente.
Berechnung von Potenzen mittels Diagonalisierung
Motivation: Die Fibonacci-Folge fn ist definiert durch die rekursive Formel f0 = 0, f1 = 1 und fn + 1 = fn + fn − 1, was gleichbedeutend ist mit
und
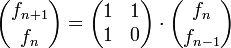 ,
,
also mit der nicht rekursiven Formel
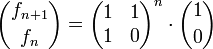 ,
,
in der die n-te Potenz einer Matrix A vorkommt.
Das Verhalten einer solchen Matrix bei Potenzierung ist nicht leicht zu erkennen; hingegen wird die n-te Potenz einer Diagonalmatrix einfach durch Potenzierung jedes einzelnen Diagonaleintrags berechnet. Wenn es nun eine invertierbare Matrix T gibt, so dass T − 1AT Diagonalform hat, lässt sich die Potenzierung von A auf die Potenzierung einer Diagonalmatrix zurückführen gemäß der Gleichung (T − 1AT)n = T − 1AnT (die linke Seite dieser Gleichung ist dann die n-te Potenz einer Diagonalmatrix). Allgemein lässt sich durch Diagonalisierung einer Matrix ihr Verhalten (bei Potenzierung, aber auch bei anderen Operationen) leichter erkennen.
Fasst man A = vfv als Matrix einer linearen Abbildung auf, so ist die Transformationsmatrix T die Basiswechselmatrix zu einer anderen Basis v', also T = vev' (wobei die Identitätsabbildung e jeden Vektor auf sich selbst abbildet). Dann ist nämlich T − 1AT = v'fv'.
Im oben genannten Beispiel lässt sich eine Transformationsmatrix T finden, so dass
eine Diagonalmatrix ist, in der der goldene Schnitt
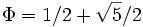 vorkommt. (Hieraus erhält man schließlich die Formel
vorkommt. (Hieraus erhält man schließlich die Formel ![f_n = 1/\sqrt5\cdot[ (1/2+\sqrt5/2)^n - (1/2-\sqrt5/2)^n ]](/pictures/dewiki/50/28281297de68f735383e4a4d974702e9.png) .)
.)Definition des Eigenwerts
Wie kommt man von der Matrix A auf die Zahl Φ? An der Diagonalmatrix erkennt man sofort, dass
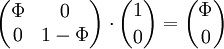 ,
,
es also einen Vektor u ungleich Null gibt, der durch Multiplikation mit der Diagonalmatrix komponentenweise vervielfacht (genauer: ver-Φ-facht) wird: (T − 1AT)u = Φu. Φ heißt wegen dieser Eigenschaft ein Eigenwert der Matrix T − 1AT (mit Eigenvektor u). Im Fall von Diagonalmatrizen sind die Eigenwerte gleich den Diagonaleinträgen.
Φ ist aber auch zugleich Eigenwert der ursprünglichen Matrix A (mit Eigenvektor Tu, denn A(Tu) = Φ(Tu)), die Eigenwerte bleiben bei Transformation der Matrix also unverändert. Die Diagonalform der Matrix A ergibt sich demnach aus deren Eigenwerten, und um die Eigenwerte von A zu finden, muss man untersuchen, für welche Zahlen x das lineare Gleichungssystem Au = xu eine von Null verschiedene Lösung u hat (oder, anders ausgedrückt, die Matrix xE − A nicht invertierbar ist).
Die gesuchten Zahlen x sind genau diejenigen, die die Determinante der Matrix xE − A zu Null machen. Diese Determinante ist ein polynomialer Ausdruck mit x (das sogenannte charakteristische Polynom von A); im Falle der oben genannten 2-mal-2-Matrix A ergibt dies die quadratische Gleichung x2 − x − 1 = 0 mit den beiden Lösungen x = Φ und x = 1 − Φ. Die zugehörigen Eigenvektoren sind Lösungen der linearen Gleichungssysteme Au = Φu bzw. Au = (1 − Φ)u, aus ihnen erhält man dann die Transformationsmatrix T.
Diagonalisierbarkeit
Ob eine Matrix diagonalisierbar ist, hängt vom verwendeten Zahlbereich ab. A ist z. B. über den rationalen Zahlen nicht diagonalisierbar, weil die Eigenwerte Φ und 1 − Φ irrationale Zahlen sind. Die Diagonalisierbarkeit kann aber auch unabhängig vom Zahlbereich scheitern, wenn nicht "genügend" Eigenwerte vorhanden sind; so hat etwa die Jordanform-Matrix
nur den Eigenwert 1 (als Lösung der quadratischen Gleichung (x − 1)2 = 0) und ist nicht diagonalisierbar. Bei genügend großem Zahlbereich (z. B. über den komplexen Zahlen) lässt sich aber jede Matrix diagonalisieren oder in Jordansche Normalform transformieren.
Da die Transformation einer Matrix dem Basiswechsel einer linearen Abbildung entspricht, besagt diese letzte Aussage, dass man zu einer linearen Abbildung bei genügend großem Zahlbereich stets eine Basis wählen kann, die "auf einfache Weise" abgebildet wird: Im Fall der Diagonalisierbarkeit wird jeder Basisvektor auf ein Vielfaches von sich abgebildet (ist also ein Eigenvektor); im Fall der Jordanform auf ein Vielfaches von sich plus evtl. den vorigen Basisvektor. Diese Theorie der linearen Abbildung lässt sich auf Körper verallgemeinern, die nicht "genügend groß" sind; in ihnen müssen neben der Jordanform andere Normalformen betrachtet werden (z. B. die Frobenius-Normalform).
Literatur
- Howard Anton: Lineare Algebra, Spektrum Akademischer Verlag GmbH Heidelberg, ISBN 3-86025-137-6.
- Albrecht Beutelspacher: Lineare Algebra, Vieweg-Verlag, ISBN 3-528-46508-5.
- Egbert Brieskorn: Lineare Algebra und analytische Geometrie, Bd.1, Vieweg-Verlag, 1983, ISBN 3-528-08561-4.
- Egbert Brieskorn: Lineare Algebra und analytische Geometrie, Bd.2, Vieweg-Verlag, 1985, ISBN 3-528-08562-2.
- Theodor Bröcker: Lineare Algebra und Analytische Geometrie, Birkhäuser Verlag, 2004, ISBN 3-7643-7144-7
- Gerd Fischer: Lineare Algebra, Vieweg-Verlag, ISBN 3-528-97217-3.
- Günter Gramlich: Lineare Algebra, Fachbuchverlag Leipzig im Carl Hanser Verlag, ISBN 3-446-22122-0.
- Günter Gramlich: Anwendungen der Linearen Algebra, Fachbuchverlag Leipzig im Carl Hanser Verlag, ISBN 3-446-22655-9.
- Klaus Jänich: Lineare Algebra, Springer-Lehrbuch, ISBN 3-540-66888-8.
- Hans-Joachim Kowalsky: Lineare Algebra, de Gruyter Lehrbuch, ISBN 3-11-008164-4.
- Burkhard Lenze: Basiswissen Lineare Algebra, W3L-Verlag, Bochum, 2006, ISBN 3-937-13781-5.
- Gilbert Strang: Lineare Algebra, Springer-Lehrbuch, ISBN 3540439498
Weblinks
Wikimedia Foundation.