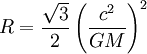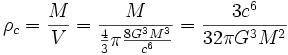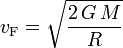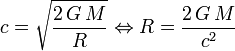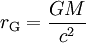Schwarzschildradius

Der Ereignishorizont liegt im einfachsten Fall an der Grenze der äußeren Schwarzschild-Metrik und stellt damit den Umfang eines Schwarzen Loches dar. Ein Beobachter, der im Unendlichen (d.h. aus einer flachen Region der Raumzeit) auf das Schwarze Loch schaut, nimmt den Ereignishorizont als eine kugelähnliche schwarze Grenzfläche wahr, aus deren Innern ihn keine Informationen erreichen können; die Bezeichnung „Ereignishorizont“ ergibt sich aus dieser Eigenschaft. Da man ein Ereignis in der allgemeinen Relativitätstheorie als einen durch Ort und Zeit festgelegten Punkt der Raumzeit definiert, stellt die Oberfläche dieser sphäroiden Region für den Beobachter einen Horizont aller Ereignisse innerhalb der Region dar. Der Radius des Ereignishorizontes heißt Schwarzschild-Radius.

Einführung

Das Gravitationsfeld eines Körpers besteht aus einer äußeren und einer inneren Lösung, wobei die äußere Lösung das Gravitationsfeld außerhalb des Körpers und die innere Lösung entsprechend das Feld im Innern des Körpers beschreibt. Bei einem Objekt, welches selbst größer als der Schwarzschild-Radius ist, liegt der Ereignishorizont innerhalb des Objekts und ist daher nicht existent, da der innere Teil nicht zur äußeren Schwarzschild-Metrik gehört; die innere Metrik enthält keine Singularitäten. Erst wenn ein Objekt kleiner als sein Schwarzschild-Radius wird, tritt der Ereignishorizont in der Raumzeit auf.

Die skalare Krümmung der Raumzeit am Ereignishorizont der Schwarzschild-Metrik beträgt

$R=\frac{\sqrt{3}}{2}\left(\frac{c^2}{G M}\right)^2$

wobei c die Lichtgeschwindigkeit, G die Gravitationskonstante und M die Masse des Schwarzen Loches sind.

Im Falle von nicht rotierenden und elektrisch nicht geladenen Schwarzen Löchern ist der Ereignishorizont die Oberfläche einer Kugel um die zentrale Singularität. Der Radius dieser Kugel ist der Schwarzschild-Radius.

Bei rotierenden Schwarzen Löchern ist der Ereignishorizont ein Ellipsoid, wobei die beiden Hauptachsen dem Schwarzschild-Radius und dem Gravitationsradius entsprechen.

Im Fernfeld gilt das klassische Gravitationsgesetz weiterhin als Näherung. Diese Näherung führt jedoch zu immer größeren Abweichungen, je weiter man sich dem Ereignishorizont annähert. In unmittelbarer Nähe des Ereignishorizonts muss dann schließlich die allgemeine Relativitätstheorie benutzt werden.

Je nach dem zugrunde liegenden Modell unseres Universums, kann auch das beobachtbare Universum einen Ereignishorizont haben. Die Beschleunigung der Ausdehnung durch die dunkle Energie würde dann dazu führen, dass Ereignisse und Objekte hinter einem bestimmten Radius in keinem kausalen Zusammenhang mehr mit uns stehen. Keinerlei Information könnte dann von einem Punkt hinter dem kosmologischen Ereignishorizont mehr zu uns dringen.

Geschichte

Pierre-Simon Laplace war der erste, der sich mit der Frage auseinandersetzte, wie groß die Anziehungskraft eines Himmelskörpers sein muss, damit Licht nicht mehr von seiner Oberfläche entweichen kann. Unter Benutzung der Newtonschen Gravitationstheorie fand er eine Beziehung zwischen dem Radius des Himmelskörpers und seiner Masse. Diesen Radius hat Karl Schwarzschild 1916 in einer allgemeinrelativistischen Rechnung wiedergefunden, daher wurde er ihm zu Ehren als Schwarzschild-Radius bezeichnet.

Schwarzschild-Radius und Gravitationsradius

Der Schwarzschild-Radius r_S einer Masse M ist gegeben durch

$r_\mathrm{S}=\frac{2 G M}{c^2}\approx M\cdot1,48\cdot10^{-27}m$.

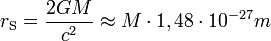Das Schwarzschild-Volumen beträgt demnach

$V_\mathrm{S}=\frac{4}{3}\pi r_\mathrm{S}^3 = \frac{4}{3}\pi \frac{8 G^3 M^3}{c^6}$,

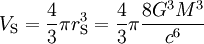womit sich eine kritische Dichte durch

$\rho_{c}=\frac{M}{V}= \frac{M}{\frac{4}{3}\pi \frac{8 G^3 M^3}{c^6}} = \frac{3 c^6}{32 \pi G^3 M^2}$

definieren lässt. Sobald eine Masse diese Dichte überschreitet, stürzt sie zu einem Schwarzen Loch zusammen.

Im Fall von nicht rotierenden und elektrisch ungeladenen Schwarzen Löchern ist der Gravitationsradius r_G gleich dem Schwarzschild-Radius. Für die Masse der Sonne beträgt er 2,952 km, für die der Erde nur noch 9 mm.

Ist das Objekt elektrisch geladen oder verfügt es über einen Drehimpuls, so sind Schwarzschild-Radius und Gravitationsradius nicht mehr identisch. (Siehe dazu die Abschnitte über rotierende und geladene Massen.)

Zu beachten ist hierbei, dass der Schwarzschildradius in der allgemeinen Relativitätstheorie nicht den Abstand vom Mittelpunkt angibt, sondern über die Oberfläche von Kugeln definiert ist. Ein kugelförmiger Ereignishorizont mit Radius r_S hat dieselbe Fläche wie eine Sphäre gleichen Radius im euklidischen Raum, nämlich A = 4πr². Aufgrund der Raumzeitkrümmung sind die radialen Abstände im Gravitationsfeld vergrößert (sprich: der Abstand zweier Kugelschalen mit – über die Kugelfläche definierten – Radialkoordinaten r₁ und r₂ ist größer als die Differenz dieser Radien).

Nichtrelativistische Betrachtungen zum Schwarzschild-Radius

Die Formel für den Gravitationsradius r_G ruhender, ungeladener Massen lässt sich auch auf naive Weise nichtrelativistisch aus folgender Überlegung ableiten, indem man für die newtonsche Fluchtgeschwindigkeit die Lichtgeschwindigkeit wählt. Dies entspricht der Annahme, dass kein Licht entkommen kann.

Die Fluchtgeschwindigkeit v_F ist diejenige Geschwindigkeit, die ein Objekt haben muss, um aus dem Gravitationsfeld eines Himmelskörpers zu entkommen. Sie beträgt

$v_\mathrm{F} = \sqrt{\frac{2\,G\,M}{R}}$

Setzt man für die Fluchtgeschwindigkeit die Lichtgeschwindigkeit c ein, so ergibt sich

$c = \sqrt{\frac{2\, G \, M}{R}}\Leftrightarrow R =\frac{2\, G\, M}{c^2}$

Da diese Herleitung nichtrelativistisch ist, ist sie jedoch physikalisch nicht korrekt. Bei der Herleitung der Schwarzschild-Metrik betrachtet man die Kugel theoretisch aus unendlicher Entfernung, also aus einem Gebiet mit flacher Raumzeit, damit man die Gleichungen durch eine newtonsche Näherung vereinfachen kann. Dass die Ergebnisse übereinstimmen ist demnach nur teilweise zufällig.

Bedeutung und Eigenschaften des Ereignishorizonts

Gravitative Rotverschiebung

Die Frequenz eines Photons wird beim Austritt aus einem Gravitationsfeld zum roten (energiearmen) Teil des Lichtspektrums verschoben, da dem Photon die entsprechende potentielle Energie verloren geht.

Nun sind die Schwarzschildkoordinaten für die Beschreibung des Gravitationsfeldes ab dem Schwarzschild-Radius jedoch ungenügend und es muss eine andere Karte benutzt werden, um die Situation zu analysieren. Unter Betrachtung der Kruskal-Szekeres-Koordinaten stellt sich heraus, dass ein Lichtsignal, welches hinter dem Schwarzschild-Radius startet, bis zum Erreichen desselben von außen aus gesehen eine unendlich lange Zeit benötigt und daher niemals austritt. Man kann sagen, dass die Rotverschiebung unendlich groß wird, wenn die Lichtquelle auf oder hinter dem Ereignishorizont sitzt.

Einfallzeit für einen außenstehenden Beobachter

Für einen außenstehenden Beobachter, der aus sicherer Entfernung zusieht, wie ein Objekt auf ein Schwarzes Loch zufällt, hat es den Anschein, als würde sich das Objekt asymptotisch dem Ereignishorizont annähern. Das bedeutet, ein außenstehender Beobachter sieht niemals, wie das Objekt den Ereignishorizont erreicht, da aus seiner Sicht dazu unendlich viel Zeit benötigt wird.

Dies ist eine Folge der am Ereignishorizont auftretenden Koordinatensingularität. Diese Singularität ist jedoch nur mathematisch und nicht physikalisch, d. h. durch passende Wahl eines anderen Koordinatensystems lässt sie sich "wegtransformieren".

Einfallzeit für einen frei fallenden Beobachter

Für einen Beobachter, der sich im freien Fall auf das Schwarze Loch zu bewegt, ist dies freilich anders. Dieser Beobachter erreicht den Ereignishorizont in endlicher Zeit. Der scheinbare Widerspruch zu dem vorherigen Ergebnis rührt daher, dass beide Betrachtungen in verschiedenen Bezugssystemen durchgeführt werden.

Ferner lässt sich in der Schwarzschild-Metrik beweisen, dass ein Objekt, welches den Ereignishorizont erreicht hat, in endlicher Zeit in die zentrale Singularität fallen muss.

Es sei noch angemerkt, dass der Ereignishorizont keine gegenständliche Grenze ist, d. h. ein frei fallender Beobachter könnte nicht direkt feststellen, wann er den Ereignishorizont passiert.

Zukunftslichtkegel

Das vorherige Resultat ist gleichbedeutend mit der Tatsache, dass die Lichtkegel sich bei der Annäherung an den Ereignishorizont immer weiter neigen. Beim Erreichen des Ereignishorizontes neigen sich die Lichtkegel schließlich so weit, dass der Zukunftslichtkegel auf die zentrale Singularität zeigt: Selbst ein Lichtstrahl kann der Singularität nicht mehr entkommen. Mit anderen Worten: Aufgrund der Neigung der Lichtkegel eines Ereignisses innerhalb oder auf dem Ereignishorizont liegt der Bereich außerhalb des Schwarzen Loches nicht mehr im Zukunftslichtkegel, d. h. ist selbst für Licht nicht mehr erreichbar.

Daraus folgt unmittelbar, dass kein Lichtsignal und damit auch keine Information aus dem Schwarzen Loch in den Außenbereich gesendet werden kann.

Hawking-Effekt

Am Ereignishorizont eines Schwarzen Loches entsteht möglicherweise die hypothetische Hawking-Strahlung aufgrund von Vakuumfluktuationen in der unmittelbaren Nähe des Ereignishorizontes. Dieser ist sogar eine zwingende Voraussetzung für die Existenz der Hawking-Strahlung.

Drehimpuls und elektrische Ladung

Rotierende Schwarze Löcher

Für rotierende Schwarze Löcher ergeben sich aus der Kerr-Metrik schwierigere Lösungen, die zu nicht kugelförmigen Ereignishorizonten und punktförmigen Singularitäten führen. Vielmehr ist der Ereignishorizont ein Rotationsellipsoid, mit den Halbachsen r_G und r_S. Dabei gilt für den maximal rotierenden Fall (unendlicher Drehimpuls ist nicht möglich) die Gleichung:

$r_\mathrm{G} = \frac{G M}{c^2}$

Hierbei ist r_G nur halb so groß wie r_S. Im nichtrotierenden Fall (Grenzfall der Schwarzschildmetrik) ist r_G gleich r_S.

Zwischen Schwarzschildradius und Gravitationsradius befindet sich um die Äquatorebene die Ergosphäre, in der die Raumzeit in zunehmendem Maße an der Rotation des Schwarzen Loches teilnimmt. Materie, Licht, Magnetfelder etc. müssen somit ebenfalls rotieren. Die Ergosphäre wird für starke Beschleunigungen z. B. von Jets in der Nähe von Schwarzen Löchern verantwortlich gemacht.

Die Singularität im Zentrum von rotierenden Schwarzen Löchern ist ringförmig.

Elektrisch geladene Schwarze Löcher

Elektrisch geladene Schwarze Löcher werden durch die Reissner-Nordström-Metrik beschrieben.