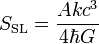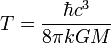Schwarzes-Loch-Paradoxon

Ein fiktives nichtrotierendes Schwarzes Loch von 10 Sonnenmassen aus 600 km Abstand gesehen, wobei dem Schwarzen Loch mit der 400-millionenfachen Erdbeschleunigung entgegengehalten werden muss, damit der Abstand konstant bleibt. Im freien Fall würde sich durch die Aberration ein anderes Bild ergeben. Die Milchstraße im Hintergrund erscheint durch die Raumzeitkrümmung verzerrt und doppelt. Der schwarze Bereich entspräche ohne Raumzeitkrümmung einem Radius von 75 km. Der Schwarzschildradius beträgt dagegen nur 29,5 km. Die Bildbreite entspricht einem Blickwinkelbereich von 90°.

Als Schwarzes Loch bezeichnet man ein astronomisches Objekt, dessen Gravitation so hoch ist, dass die Fluchtgeschwindigkeit für dieses Objekt ab einer gewissen Grenze, dem Ereignishorizont, höher liegt als die Lichtgeschwindigkeit.

Der Ausdruck „Schwarzes Loch“ wurde 1967 von John Archibald Wheeler geprägt und verweist auf den Umstand, dass auch elektromagnetische Wellen, wie etwa sichtbares Licht, den Ereignishorizont nicht verlassen können und es einem menschlichen Auge daher vollkommen schwarz erscheint.

Mathematische Beschreibung

Ein Schwarzes Loch lässt sich durch lediglich drei physikalische Kenngrößen vollständig beschreiben (sogenannte Haarlosigkeit Schwarzer Löcher): Masse, Drehimpuls und Elektrische Ladung. Die Multipolmomente entfallen. Es gibt also folgende Klassen:

• Schwarze Löcher, die keine elektrische Ladung tragen (Q = 0) und nicht rotieren (L = 0), werden durch die Schwarzschild-Metrik beschrieben.
• Schwarze Löcher, die keine elektrische Ladung tragen (Q = 0) und rotieren (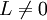$L\neq 0$), werden durch die Kerr-Metrik beschrieben.
• Schwarze Löcher, die elektrisch geladen sind (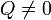$Q\neq 0$) und nicht rotieren (L = 0), werden durch die Reissner-Nordström-Metrik beschrieben.
• Schwarze Löcher, die elektrisch geladen sind (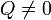$Q\neq 0$) und rotieren (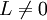$L\neq 0$), werden durch die Kerr-Newman-Metrik beschrieben.

Rotierendes Schwarzes Loch

Das rotierende Schwarze Loch ist die allgemeine Form dieses astrophysikalischen Phänomens. Schwarze Löcher verursachen, bedingt durch ihre enorme Gravitation, eine entsprechend große Veränderung der geometrischen Struktur von Raum und Zeit (kurz: Raumzeitkrümmung). In der Umgebung eines ruhenden Schwarzen Lochs wird die Raumzeit extrem gekrümmt. Während bei ruhenden Schwarzen Löchern nur punktförmige Singularitäten auftreten, tritt bei einem rotierenden Schwarzen Loch eine kreisförmige oder Ringsingularität auf.

Als rotierende Schwarze Löcher werden solche bezeichnet, die einen Eigendrehimpuls besitzen. Dadurch verändert sich bei ihnen die geometrische Struktur der Raumzeit. Anstatt diese nur zu krümmen, wird sie mit dem Schwarzen Loch „mitgerissen“ und dadurch verzerrt. Der Raum wird in der Drehrichtung des Schwarzen Lochs mitgedreht. Diese Raumzeitkrümmung erfolgt in der Umgebung eines rotierenden Schwarzen Lochs nicht wie bei einem ruhenden in Form einer Kugel, sondern so verzerrt, dass sie in der Form eines Ellipsoids auftritt.

Der Ereignishorizont bezeichnet die äußere Grenze des Schwarzschildradius. Bei ruhenden Schwarzen Löchern entspricht der Ereignishorizont der Form einer Kugel. Durch die Veränderung der geometrischen Struktur der Raumzeit wird auch die Struktur des Ereignishorizontes bei rotierenden Schwarzen Löchern verändert. Dort treten ein äußerer sowie ein innerer Ereignishorizont auf. Der innere Ereignishorizont entspricht der Oberfläche einer Kugel, die Form des äußeren Ereignishorizonts ist meist verzerrt, seine Oberfläche entspricht der Form eines an den Polen abgeplatteten Rotationsellipsoids.

Zwischen dem inneren und dem äußeren Ereignishorizont befindet sich die Ergosphäre. Befindet sich ein Objekt innerhalb dieses Raumes, rotiert es mit dem Schwarzen Loch. Die Rotationsgeschwindigkeit des Teilchens entspricht dann der Rotationsgeschwindigkeit des Schwarzen Loches oder der Ergosphäre an diesem Punkt. Ein Teilchen, das sich in der Ergosphäre befindet, wird nicht zwingend in die zentrale Singularität hineingezogen. Bewegt sich das Teilchen in der Ergosphäre nach außen, also in Richtung der statischen Grenze, kann es dem Gravitationsfeld des rotierenden Schwarzen Lochs dennoch nicht entfliehen, es bleibt gefangen. Dasselbe gilt auch für nahezu alle Formen von Energie. Die Ausdehnung der Ergosphäre entspricht dem äußeren Ereignishorizont. Hier ist die Raumzeitkrümmung wieder (annähernd) null.

Schwarze Löcher im Universum

Gravitationsfeld und Ereignishorizont

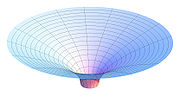Äußere Schwarzschildlösung.

Das Gravitationsfeld kugelförmiger, nichtrotierender und elektrisch ungeladener Körper wird durch die äußere Schwarzschild-Metrik beschrieben. Sie gilt nicht nur für Schwarze Löcher, sondern für alle Körper mit diesen Eigenschaften und stellt für Sterne oder Planeten meist eine gute Näherung dar. Es ist ein weit verbreiteter Irrtum, dass das Gravitationsfeld eines Schwarzen Loches bzw. die von ihm hervorgerufene Krümmung von Raum und Zeit, bei üblichen Entfernungen von außerordentlich großer Stärke sei. Da sowohl Schwarze Löcher als auch Sterne von derselben Metrik beschrieben werden, würde sich am Gravitationsfeld im Sonnensystem nichts ändern, wenn man die Sonne durch ein Schwarzes Loch gleicher Masse ersetzt. Lediglich in unmittelbarer Umgebung des schwarzen Loches wächst die Gravitationsbeschleunigung sehr stark an. Die innere Schwarzschild-Metrik beschreibt das Gravitationsfeld innerhalb eines solchen Körpers.

Aus der inneren Region des Schwarzen Loches kann keine Form von Energie entweichen, da selbst ein Photon von außen aus gesehen unendlich lange braucht, um den Ereignishorizont zu erreichen oder gar zu verlassen. Von der Position eines in unendlicher Entfernung stationierten Beobachters, d. h. einem Beobachter, der sich selbst nicht im Gravitationsfeld des Schwarzen Loches befindet, dauert es umgekehrt auch unendlich lange, bis ein Objekt in das Schwarze Loch hineinfällt. Im Falle der Schwarzschild-Metrik wird die Entfernung des Ereignishorizontes von der inneren Singularität als Schwarzschildradius bezeichnet. Solange ein Objekt größer als der Schwarzschildradius ist, hat es keinen Ereignishorizont. Da dort jedoch die innere Schwarzschild-Metrik gilt und diese weder eine Singularität, noch einen Ereignishorizont enthält, gibt es Letzteren in diesem Fall auch dann nicht, wenn man sich durch das Objekt bewegen und diesen Radius erreichen würde. Der Ereignishorizont tritt erst dann in der äußeren Schwarzschild-Metrik in Erscheinung, wenn das Objekt kleiner als der Schwarzschildradius wird. In räumlicher und zeitlicher Hinsicht würde ein Beobachter, der durch den Ereignishorizont hindurch fällt, trotz alledem selbst nichts Besonderes bemerken.

Die Größe des Schwarzschildradius beträgt für ein Schwarzes Loch von einer Sonnenmasse etwa 2,9 km, für ein Objekt von einer Erdmasse etwa 9 Millimeter.

Die Dichte, bis zu der Materie komprimiert werden muss, um durch ihre Gravitationskraft zu einem Schwarzen Loch zu kollabieren, ist umgekehrt proportional zum Quadrat der Masse. Objekte mit weniger als etwa 1,5 Sonnenmassen (Chandrasekhar-Masse) können nicht durch einen Gravitationskollaps zu einem Schwarzen Loch kollabieren, da der abstoßende Entartungsdruck in entarteter Materie einen Kollaps verhindert.

Beobachtung von Schwarzen Löchern

Akkretionsscheibe eines Röntgendoppelsterns.

Ein schwarzes Loch zieht zwischen dem Betrachter und einer Galaxie im Hintergrund vorbei. (Fiktive Simulation)

Eine direkte Beobachtung von Schwarzen Löchern gilt als praktisch unmöglich. Moderneren Theorien zufolge sind Schwarze Löcher zwar möglicherweise in der Lage, Energie in Form von sogenannter Hawking-Strahlung abzugeben. Sollte dies zutreffen, würde das bedeuten, dass Schwarze Löcher allmählich „verdampfen“, wobei dieser Prozess umso schneller verläuft, je geringer die Masse des Schwarzen Loches ist. Doch die Hawking-Strahlung wäre so energiearm, dass sie vom üblichen Hintergrund nicht zu unterscheiden wäre. Außerdem ist das Schwarze Loch selbst mit nur wenigen Kilometern Durchmesser auf kosmische Entfernungen viel zu klein.

Beobachtet werden dagegen Materiestrahlen. In diesen Jets wird ein Teil der verschlungenen Materie in Energie umgewandelt und als Gammastrahlung oder Teilchenstrom weggeschleudert. Spektakulär beobachtet wurde das Ende 2007 beim Schwarzen Loch, das im Zentrum der Galaxie 3C321 liegt.

Es gibt viele Arten von aktiven Galaxienkernen, wie etwa Quasare, die eine hohe und sehr variable Leuchtkraft aufweisen; diese können durch zahlreiche Effekte entstehen. Einer der energiereichsten Prozesse findet statt, wenn Materie mit hoher Geschwindigkeit auf ein Schwarzes Loch zufällt, dabei erhitzt und einen Teil seiner Masse in Form von Gammastrahlung emittiert. Siehe hierzu auch: Gammastrahlenexplosion.

Kinematischer Nachweis

Beim kinematischen Nachweis wird die Bahn und die Geschwindigkeit von Sternen, die das schwarze Loch umkreisen, als Nachweis herangezogen^[1]. Die Vermessung der Bahn des Sterns S2, der Sgr A* auf einer Kepler-Bahn mit ca. 5000 km/s umkreist, erlaubte sehr genaue Aussagen über die Massenkonzentration im Zentralbereich von Sgr A*. Eine weitere kinematische Methode ist die Ermittlung der Dopplerverschiebung und des Abstands von Materiewolken um ein vermutetes Schwarzes Loch.

Eruptiver Nachweis

Sterne, die dem Gezeitenradius eines Schwarzen Lochs zu nahe kommen, können durch die auftretenden Gezeitenkräfte zerrissen werden und dabei eine charakteristische Röntgenstrahlung freisetzen.

Akkretiver Nachweis

Interstellares Gas, welches von einem schwarzen Loch aufgesammelt wird, emittiert Strahlung über alle Spektralbereiche und gilt als Nachweis eines zentralen Schwarzen Lochs^[2].

Arten von Schwarzen Löchern

Man unterteilt Schwarze Löcher je nach der Art der Entstehung und aufgrund ihrer Masse in verschiedene Klassen:

Art	Masse	Größe
Supermassereiches Schwarzes Loch	~10.000–109 MSonne	~0,001–10 AU
Mittelschweres Schwarzes Loch	~1000 MSonne	~103 km = RErde
Stellares Schwarzes Loch	~10 MSonne	~30 km
Primordiales Schwarzes Loch	bis zu ~MMond	bis zu ~0,1 mm

Stellare Schwarze Löcher

Stellare Schwarze Löcher stellen den Endzustand der Entwicklung massereicher Sterne dar. Sterne, deren Anfangsmasse kleiner als acht Sonnenmassen ist, können nicht zu einem Schwarzen Loch werden. Sie beenden ihr Leben als vergleichsweise unspektakulär auskühlender Sternenrest (Weißer Zwerg). Sterne, deren Anfangsmasse acht Sonnenmassen übersteigt (etwa Blaue Riesen), durchlaufen am Ende ihres Lebens die höheren Stufen der Nukleosynthese bis zum Siliciumbrennen.

Sie explodieren dann in einer Kernkollaps-Supernova, wobei der übrig bleibende Sternenrest zu einem Schwarzen Loch kollabiert, sofern er noch mehr als 2,5 Sonnenmassen besitzt (Tolman-Oppenheimer-Volkoff-Grenze). Ansonsten können Sterne bis zur fünfzehnfachen Sonnenmasse abhängig davon, wie viel Masse sie als Supernova verlieren, auch als Neutronenstern enden, wenn die verbleibende Masse zwischen 1,5 und 2,5 Sonnenmassen liegt. Neutronensterne können sich – beispielsweise als kompakter Begleiter in einem Röntgendoppelstern – durch die Akkretion weiterer Materie auch im Nachhinein noch zu Schwarzen Löchern entwickeln.

Rekordhalter bei der Masse stellt aktuell das stellare Schwarze Loch in der Zwergengalaxie IC 10 im Sternbild Kassiopeia mit der 24- bis 33-fachen Sonnenmasse dar. Es ist Teil eines Doppelsternsystems. Das schwarze Loch wurde indirekt durch die in ihrer Stärke schwankende Röntgenstrahlung des begleitenden Sterns entdeckt, was ein Hinweis auf ein periodisch die Quelle verdeckendes Objekt sein kann. Berechnungen aus Daten des Satelliten Swift, sowie des Gemini-Teleskops auf Hawaiʻi bestätigten die Vermutungen. ^[3].

Mittelschwere Schwarze Löcher

Mittelschwere Schwarze Löcher entstehen möglicherweise in Folge von Sternenkollisionen und -verschmelzungen. Ihre Existenz ist noch nicht sicher erwiesen, allerdings veröffentlichten Forscher Anfang 2004 Ergebnisse einer Untersuchung von Nachbargalaxien mit dem Weltraumteleskop Chandra, in der sie Hinweise auf Mittelschwere Schwarze Löcher in sogenannten ultrahellen Röntgenquellen (ULX) fanden. Inzwischen gibt es allerdings aufgrund neuerer Beobachtungen mit dem VLT und dem Subaru-Teleskop starke Zweifel daran, dass ULX mittelschwere Schwarze Löcher sind^[4]. Ein neuer Kandidat für ein solches wird im Zentrum einer Zwerg-Seyfert-Galaxie vermutet^[5]. Wird in einem Röntgendoppelstern einer der Partner zu einem Schwarzen Loch, kann im weiteren Verlauf der Entwicklung sehr viel Masse vom leichteren Partner auf das entstandene Schwarze Loch abfließen. Die meisten Schwarzen Löcher schaffen es jedoch nicht, mehr als einige Sonnenmassen Material aus der Umgebung einzufangen. Welche Bedingungen für die mögliche Entstehung mittelschwerer Schwarzer Löcher notwendig sind, ist unklar. Als derzeit einzige Kandidaten für solche Objekte werden die Zentren der Kugelsternhaufen Omega Centauri in der Milchstrasse und G1 in der Andromeda Galaxie gewertet.^[6]

Supermassereiche Schwarze Löcher

Galaktisches Zentrum

Supermassereiche (auch supermassiv genannte) Schwarze Löcher können die millionen- bis milliardenfache Sonnenmasse haben und befinden sich vermutlich in den Zentren der meisten Galaxien. Wie sie entstanden sind und wie ihre Entstehung mit der Entwicklung der Galaxien zusammenhängt, ist Gegenstand aktueller Forschung.

So wird hinter der starken Radioquelle Sagittarius A* (kurz Sgr A*) im Zentrum der Milchstraße ein supermassives Schwarzes Loch von 4,3 Millionen Sonnenmassen vermutet.^[7] Vor wenigen Jahren lag die Massenabschätzung, die auf der Beobachtung von Gaswolken (z. B. der sogenannten Mini-Spirale) fußte, noch bei etwa 2,7 Mio. Sonnenmassen. Dank verbesserter Auflösung und Empfindlichkeit der Teleskope konnte eine genauere Masse für das Schwarze Loch im Zentrum der Galaxis angegeben werden, z. B. durch Analyse der Bahnkurven der sog. S0-Sterne, wobei die 0 lediglich bedeutet, dass die Umlaufbahnen der Sterne unter einem relativen Winkel von einer Bogensekunde zu beobachten sind (entsprechendes gilt für die S1, S2 Sterne usw.).

In ^[8] wird dargelegt, dass ein oberes Massenlimit für Schwarze Löcher existiert und bei etwa 10 Milliarden Sonnenmassen liegen muss. Die Begründung liegt, anschaulich erklärt, darin, dass die hineinstürzende Materie durch die Gravitationskraft eines solchen supermassiven Schwarzen Lochs derart beschleunigt wird, dass sich ein stabiler Orbit außerhalb des Schwarzschild-Radius ergibt. Zusätzlich wirken auch die elektromagnetische Strahlung und die "Materiewinde", die von der Materie in der Akkretionsscheibe ausgestrahlt werden, als "Widerstand" gegen weiter einfallende Materie, so dass sich letztlich ein Gleichgewicht zwischen einfallender und abgestoßener Materie einstellt.

Primordiale Schwarze Löcher

Anfang der 1970er Jahre stellte Stephen W. Hawking als Erster die Vermutung auf, neben den durch Supernovae entstandenen Schwarzen Löchern könnte es auch so genannte primordiale Schwarze Löcher geben. Das sind Schwarze Löcher, die sich bereits im Urknall in Raumbereichen gebildet haben, in denen die lokale Massen- und Energiedichte genügend hoch war (rechnet man die ständig abnehmende Materiedichte im Universum zurück, so findet man, dass sie in der ersten tausendstel Sekunde nach dem Urknall die Dichte des Atomkerns überstieg). Auch der Einfluss von Schwankungen der gleichmäßigen Dichteverteilung (siehe hierzu kosmische Hintergrundstrahlung) im frühen Universum war für die Bildung von primordialen Schwarzen Löchern ausschlaggebend, ebenso die beschleunigte Expansion während der Inflationsphase nach dem Urknall. Damals könnten sich kleine Schwarze Löcher mit einer Masse von etwa 10¹² Kilogramm gebildet haben. Seit Mitte der 1990er Jahre wird diskutiert, ob die kürzesten auf der Erde gemessenen Gammastrahlungsausbrüche von verstrahlenden primordialen Schwarzen Löchern stammen könnten, denn deren berechnete Lebensdauer liegt in der Größenordnung des Alters des heutigen Universums.

Aus seinen Überlegungen über kleine Schwarze Löcher folgerte Hawking im Jahre 1974 die Existenz der nach ihm benannten Hawking-Strahlung, dass also Schwarze Löcher Materie nicht nur schlucken, sondern auch wieder freisetzen können. Obwohl die Existenz von primordialen Schwarzen Löchern keineswegs gesichert ist, haben sich also allein aus hypothetischen Betrachtungen wertvolle neue Erkenntnisse im Bereich der Kosmologie, der Quantenphysik und der Relativitätstheorie ergeben.

Schwarze Mini-Löcher

Einigen so genannten Vereinheitlichenden Theorien zufolge, wie z. B. der Stringtheorie, könnte es bald möglich sein, extrem kurzlebige Schwarze Mini-Löcher im Labor (bzw. in Teilchenbeschleunigern) herzustellen.

Sollte es sich erweisen, dass dies tatsächlich so ist, so ist aber gleichzeitig davon auszugehen, dass sich diese Schwarzen Mini-Löcher ebenfalls bei Teilchenkollisionen von kosmischer Strahlung mit Molekülen in der Hochatmosphäre bilden (seit Milliarden Jahren) und daher keine Gefahr darstellen können.

Nächste Schwarze Löcher in der Milchstraße

Neben dem zentralen Schwarzen Loch in unserer Galaxis, nämlich Sagittarius A* mit einer Masse von 3 bis 4 Millionen Sonnen, gibt es eine Reihe weiterer vermuteter kleiner Schwarzer Löcher, die in der Milchstraße verteilt sind und eine Masse von mehreren bis einem Dutzend Sonnen aufweisen. Sie alle sind Teilnehmer in Doppel- oder Mehrfachsternsystemen, ziehen von ihrem Partner scheinbar in einer Akkretionsscheibe Materie ab und strahlen im Röntgenbereich.^[9][10]

Name	Masse (Sonnenmassen)	Masse Partner (Sonnenmassen)	Umlaufzeit (Tage)	Entfernung von der Erde (Lichtjahre)
V4641 Sagittarii	3−10	?	?	~1600
A0620-00	9−13	2,6−2,8	0,33	~3500
GRO J1655-40	6−6,5	2,6−2,8	2,8	5000−10.000
XTE J1118+480	6,4−7,2	6−6,5	0,17	6200
Cyg X-1	7−13	0,25	5,6	6000−8000
GRO J0422+32	3−5	1,1	0,21	~8500
GS 2000+25	7−8	4,9−5,1	0,35	~8800
V404 Cyg	10−14	6,0	6,5	~10.000
XTE J1650-500[11]	3,8	?	?	~10.000
GX 339-4		5−6	1,75	~15.000
GRS 1124-683	6,5−8,2		0,43	~17.000
XTE J1550-564	10−11	6,0−7,5	1,5	~17.000
XTE J1819-254	10−18	~3	2,8	< 25.000
4U 1543-475	8−10	0,25	1,1	~24.000
Sgr A*	4,3 Mio.	−	−	~25.000

Weitere beobachtete Schwarze Löcher

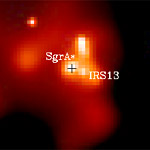
Neueste Forschungsergebnisse zeigen, dass sich in der Sternengruppe IRS 13, die nur 3 Lichtjahre von Sgr A* entfernt liegt, ein zweites Schwarzes Loch mit vergleichsweise geringen 1300 Sonnenmassen befindet. Es ist derzeit nicht geklärt, ob es sich in Zukunft mit Sgr A* vereinigen wird, oder ob es sich auf einer stabilen Umlaufbahn befindet, oder sich sogar von ihm entfernt.

In der Galaxie NGC 6240 befinden sich zwei Schwarze Löcher, die sich im Abstand von 3000 Lichtjahren umkreisen und in einigen hundert Millionen Jahren verschmelzen werden.

Das erste Schwarze Loch außerhalb unserer Galaxie wurde 1982 in der etwa 150.000 Lichtjahre entfernten Großen Magellanschen Wolke nachgewiesen und bildet eine Komponente des Röntgendoppelsterns LMC X-3.^[12]

Theoretische Betrachtungen

Schwarze Löcher in der allgemeinen Relativitätstheorie

Formell ergibt sich ein Schwarzes Loch aus einer speziellen Vakuumlösung der allgemeinen Relativitätstheorie, der sogenannten Schwarzschild-Lösung (nach Karl Schwarzschild, der diese Lösung als erster fand), bzw. für rotierende und elektrisch geladene Schwarze Löcher aus der Kerr-Newman-Lösung. Eine „Vakuumlösung“ ist eine Lösung der Vakuumfeldgleichungen – also etwa im Außenraum um einen Stern herum, wo sich näherungsweise keine Materie aufhält und damit der Energie-Impuls-Tensor verschwindet. Im Zentrum des Schwarzen Loches befindet sich eine physikalische Singularität; die Krümmung der Raumzeit wird an dieser Stelle unendlich groß und die Gleichungen der Relativitätstheorie versagen, weil für die Beschreibung dieses Ortes eine TOE notwendig ist. Die ganze Masse des Schwarzen Loches ist in einem Punkt (bei rotierenden Schwarzen Löchern in einem Ring) ohne Ausdehnung konzentriert. Nach heutigem Stand des Wissens kann dies zustande kommen, weil die Gravitation in einem Schwarzen Loch so groß ist, dass keine der anderen drei Grundkräfte der Physik der Komprimierung entgegenwirken kann. Die gesamte Materie stürzt in sich zusammen und konzentriert sich in der Singularität. Aus diesem Grund ist die Dichte der Singularität unendlich.

Die Grenze, ab der keine Information mehr zu einem im Unendlichen befindlichen Beobachter gelangen kann, heißt Ereignishorizont, ihr Radius ist der Schwarzschildradius. Da ein nichtrotierendes Schwarzes Loch von außen gesehen kugelförmig ist, hat auch der Ereignishorizont die Form einer Kugeloberfläche. Der Umfang dieser Kugel ist das 2π-fache des Schwarzschildradius.

Für rotierende und/oder geladene Schwarze Löcher ist der Ereignishorizont nicht mehr kugelförmig, und seine Größe ist auch nicht mehr durch den Schwarzschildradius gegeben. Rotierende Schwarze Löcher haben zudem außerhalb des Ereignishorizonts einen Ergosphäre genannten Bereich, in dem es einem Objekt nicht möglich ist, nicht mit dem Schwarzen Loch mitzurotieren.

Schwarze Löcher können bei gegebener Masse nicht beliebig große Ladung und nicht beliebig großen Drehimpuls besitzen. Setzt man in die entsprechenden Lösungen der allgemeinen Relativitätstheorie eine zu hohe Ladung und/oder einen zu hohen Drehimpuls ein, so ergibt sich statt eines Schwarzen Loches eine sogenannte nackte Singularität: Es bildet sich zwar eine zentrale Singularität aus, jedoch ist diese nicht von einem Ereignishorizont umgeben. Man kann allerdings zeigen, dass man aus einem normalen Schwarzen Loch keine nackte Singularität machen kann, indem man Ladung und/oder Drehimpuls zuführt, da die gleichzeitig zugeführte Energie seine Masse ausreichend erhöhen würde, um eine nackte Singularität zu verhindern.

Der Ereignishorizont wird bei Sternen, die zu Schwarzen Löchern kollabierten, von Lichtstrahlen begrenzt. Diese Lichtstrahlen sind die letzten, die noch nicht von der Gravitation des Schwarzen Loches angezogen wurden.

Die „Hauptsätze der Schwarzloch-Dynamik“

Für Schwarze Löcher folgen aus der allgemeinen Relativitätstheorie Gesetze, die auffallend jenen der Thermodynamik gleichen. Schwarze Löcher verhalten sich ähnlich wie ein Schwarzer Strahler; sie haben also eine Temperatur. Es gelten im Einzelnen die folgenden Gesetze:

Der Erste Hauptsatz der „Schwarzloch-Dynamik“ ist, wie in der gewöhnlichen Thermodynamik, der Energieerhaltungssatz, jedoch unter Berücksichtigung der relativistischen Energie-Masse-Äquivalenz. Zusätzlich gelten die anderen Erhaltungssätze der Mechanik und Elektrodynamik: Neben der Energie bleiben Impuls, Drehimpuls und Ladung erhalten.

Der Zweite Hauptsatz der „Schwarzloch-Dynamik“ – von Stephen W. Hawking postuliert – besagt, dass die Summe der Flächen der Ereignishorizonte niemals abnehmen kann, egal was mit den Schwarzen Löchern passiert. Dies gilt nicht nur, wenn Materie in das Schwarze Loch fällt (was dessen Masse – und damit dessen Ereignishorizont – vergrößert), sondern auch beispielsweise für die Verschmelzung zweier Schwarzer Löcher und für jeden anderen denkbaren Prozess. Dies entspricht dem zweiten Hauptsatz der Thermodynamik, wobei die Fläche des Ereignishorizonts die Rolle der Entropie übernimmt. Die Entropie des Schwarzen Lochs ist 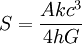$S = \frac{A k c^3}{4 h G}$ (Erklärung der Formelzeichen: siehe unten). Schwarze Löcher haben die höchste Entropie aller bekannten physikalischen Systeme gleicher Masse.

Hawking-Strahlung

Hauptartikel: Hawking-Strahlung

Quantentheoretische Überlegungen zeigen, dass jedes Schwarze Loch auch Strahlung abgibt. Wie im Hauptartikel erläutert, findet dabei kein Materie- oder Energietransport aus dem Inneren des Schwarzen Lochs statt. Tatsächlich entstehen Paare von virtuellen Teilchen in der unmittelbaren Umgebung, von denen nur eines in das Schwarze Loch gerät und dort anschaulich als negative Energie verrechnet werden muss und somit die Gesamtenergie des Schwarzen Lochs vermindert. Von außen betrachtet sieht es allerdings so aus, als würde das Schwarze Loch „verdampfen“ und somit langsam kleiner werden. Die beobachtbare Temperatur bzw. Strahlungsfrequenz hängt umgekehrt proportional von der Masse ab. Dies bedeutet für sehr kleine, primordiale Schwarze Löcher, dass sie sehr heiß sein und dementsprechend stark strahlen müssten, aber auch schnell verdampfen sollten, eventuell so schnell, dass sie bereits alle zerstrahlt sein könnten. Die dabei entstehende Strahlung ist sehr charakteristisch und kann vielleicht als Nachweis solcher Löcher dienen. Andersherum gibt die Tatsache, dass man diese Strahlung bisher nicht gesehen hat, eine Obergrenze für ihre Anzahl. Umgekehrt gilt schon für normalgroße stellare Schwarze Löcher, dass sie sehr kalt sind und damit nur noch wenig an Masse verlieren würden. Ein Schwarzes Loch mit einer Masse von zehn Sonnenmassen hat eine Temperatur von nur wenigen milliardstel Kelvin und ist damit viel kälter als die Umgebung. Effektiv werden sie also sogar von ihrer Umgebung aufgewärmt und gewinnen daher Masse hinzu.

Entropie und Temperatur

Hawking erkannte 1974, nach Vorarbeiten des israelischen Physikers Jacob Bekenstein, dass Schwarze Löcher eine Entropie und somit auch eine Temperatur haben. Die Entropie S eines Schwarzen Lochs ist proportional zur Oberfläche A seines Horizonts und sonst nur von Naturkonstanten abhängig.

$S_\mathrm{SL}=\frac{ A k c^3}{ 4 \hbar G}$

$T=\frac{ \hbar c^3}{8\pi kGM}$

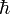wobei $\hbar$ das plancksche Wirkungsquantum bzw. hier diracsche Konstante, c die Lichtgeschwindigkeit, π die Kreiszahl Pi, k die Boltzmannkonstante, G die Gravitationskonstante und M die Masse ist.

Lebensdauer

Da nach Hawking ein Schwarzes Loch stetig Energie in Form von Hawking-Strahlung verliert, wird es nach einer bestimmten Zeitspanne Δt vollständig zerstrahlt sein, sofern es während dieser Zeitspanne keine neue Masse aufnehmen kann. Diese Zeitspanne berechnet sich durch

$\Delta t=\frac{M^3}{3\Lambda_t}$,

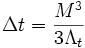wobei M die Masse des Schwarzen Loches zu Beginn der Zeitspanne und Λ_t eine Konstante mit 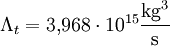$\Lambda_t = 3{,}968 \cdot 10^{15} \frac{\mathrm{kg}^3}{\mathrm{s}}$ ist.

No-Hair-Theorem und Informationsverlustparadoxon

Für ein Schwarzes Loch gilt ein so genanntes Eindeutigkeits-Theorem von Werner Israel. Dieses besagt, dass ein Schwarzes Loch vollständig durch Masse, elektrische Ladung und Drehimpuls charakterisiert ist. Das veranlasste John Archibald Wheeler zur Aussage „Schwarze Löcher haben keine Haare“. Man spricht deshalb vom No-Hair-Theorem. Weitere Informationen aus dem Inneren seien nicht zu erhalten, auch nicht durch die Hawking-Strahlung, da sie rein thermisch ist.

Verschiedentlich wurde angenommen, dass Schwarze Löcher einen Verlust an Information erzwingen, da die bei der Auflösung entstehende Hawking-Strahlung keine Informationen mehr über die beliebig komplizierte Entstehungsgeschichte des Schwarzen Lochs enthält. Diese Verletzung der Unitarität der Zeitentwicklung, das heißt, dass, entgegen allen sonstigen Vorgängen in der Quantenmechanik, ein Zeitpfeil ausgezeichnet sei, wird auch als Schwarzes-Loch-Paradoxon bezeichnet.

Prominente Vertreter dieser Sicht waren Kip Thorne und anfangs auch Stephen Hawking, der jedoch auf der 17. „International Conference on General Relativity and Gravitation“ (18.–23. Juli 2004 in Dublin) seine frühere Meinung änderte und erklärte, dass Schwarze Löcher doch „Haare“ haben könnten. Weiterhin nehmen unter anderem Roger Penrose, John Preskill und Juan Maldacena an, dass zumindest gewisse Informationen zusätzlich nach außen dringen könnten.

Auch in seinem Buch „Das Universum in der Nussschale“ äußert Stephen Hawking die Annahme, dass Schwarze Löcher bei ihrem Ableben die gesammelte Information wieder abgäben.

Alternativen

Aufgrund der Probleme mit der Singularität der Raumzeit und dem Informationsparadoxon bei einem Schwarzen Loch wurden einige alternative Modelle für ultrakompakte dunkle Objekte vorgeschlagen. Da diese Modelle keine mit heutigen Mitteln beobachtbaren Vorhersagen machen, über die sie sich von einem Schwarzen Loch unterscheiden ließen, ist die Akzeptanz denkbar gering. Ein bekanntes Beispiel sind die Gravasterne.

Geschichte

Schon 1783 spekulierte der britische Naturforscher John Michell über „dunkle Sterne“, deren Gravitation ausreicht, um Licht gefangen zu halten. Die gleiche Idee hatte 1796 Pierre Simon Laplace in seiner Exposition du Système du Monde. Diese Ideen bewegten sich ganz innerhalb der Newtonschen Physik.

Nach der Veröffentlichung Albert Einsteins 1915, in der er die Feldgleichungen der Allgemeinen Relativitätstheorie aufstellte, berechnete Karl Schwarzschild 1916 erstmals die Größe und das Verhalten eines Schwarzen Loches. Dieser Name wurde aber erst 1968 von John Archibald Wheeler eingeführt, davor sprach man teilweise von „gefrorenen Sternen“, da am Rand des Loches die Zeit für äußere Beobachter aufgrund der gravitativen Zeitdilation stehen bleibt. Robert Oppenheimer wies 1939 zusammen mit Robert Serber und George Michael Volkoff anhand von Modellrechnungen nach, dass beim Kollaps eines großen Sterns ein Schwarzes Loch entstehen muss. 1974 zeigte Stephen Hawking, dass Schwarze Löcher eine Strahlung abgeben, die Hawking-Strahlung. Nachdem Hawking bereits 1971 herausgefunden hatte, dass der Ereignishorizont niemals kleiner wird, veröffentlichten 2002 Abhay Ashtekar und Badri Krishnan eine Lösung für die Beschreibung wachsender Schwarzer Löcher, ohne dabei eine Näherung nutzen zu müssen, was bei einsteinschen Feldgleichungen der allgemeinen Relativitätstheorie nur selten gelingt.

Sonstiges

• Schwarze Löcher werden in der Science-Fiction-Literatur oft als Mittel zu überlichtschnellem Transport verwendet, so z. B. in Stanisław Lems Fiasko oder in einer ganzen Reihe von Perry-Rhodan-Romanen.
• Die mythische Schwärze Schwarzer Löcher ist ein dramaturgisches Mittel im Film „Das schwarze Loch“ (1979) mit Maximilian Schell und Anthony Perkins in den Hauptrollen.
• Schwarze Löcher werden auch in manchen Serien, wie z. B. in der Serie „Stargate“ als ultimative Energiequellen verwendet, indem sie Energie an andere Objekte abgeben, weil sie dauerhaft Energie abstrahlen.

Siehe auch

• Machsches Prinzip
• Weißes Loch

Literatur

• Kip S. Thorne: Gekrümmter Raum und verbogene Zeit. Droemer Knaur, ISBN 3-426-77240-X, englisch: Black Holes and Time Warps: Einstein’s Outrageous Legacy. W. W. Norton & Company, ISBN 0-393-31276-3.
• Max Camenzind: Von der Rekombination zur Bildung Schwarzer Löcher. In: Sterne und Weltraum. 44/3/2005. Vereinigung der Sternfreunde, S. 28–38, ISSN 0039-1263.
• Stephen W. Hawking: Eine Kurze Geschichte der Zeit. Rowohlt Tb., Reinbek bei Hamburg 1988, ISBN 3-499-60555-4.
• Stephen W. Hawking: Das Universum in der Nussschale. 2. Auflage. Dtv, München 2004, ISBN 3-423-34089-4.
• Bernard J. Carr, Steven B. Giddings: Schwarze Löcher im Labor. In: Spektrum der Wissenschaft 09/05.
• Ute Kraus: Reiseziel: Schwarzes Loch. In: Sterne und Weltraum 11/05.
• Rüdiger Vaas: Tunnel durch Raum und Zeit, Franckh-Kosmos, Stuttgart 2006 (2. Aufl.), ISBN 3-440-09360-3.
• Stephen W. Hawking: Die kürzeste Geschichte der Zeit. Rowohlt Tb., Reinbek bei Hamburg 2006, ISBN 3-499-62197-5.
• Mitchell Begelman, Martin Rees: Schwarze Löcher im Kosmos - Die magische Anziehungskraft der Gravitation. Spektrum Akademischer Verlag, ISBN 3-8274-1044-4.
• Fulvio Melia: The galactic supermassive black hole. Princeton Univ. Pr., Princeton 2007, ISBN 0-691-09535-3
• Pietro Fré: Classical and quantum black holes. Inst. of Physics Publ., Bristol 1999, ISBN 0-7503-0627-0
• Hyun Kyu Lee, (et al.): Black hole astrophysics 2002. World Scientific, Singapore 2002, ISBN 981-238-124-4
• Valerij P. Frolov, (et al.): Black hole physics - basic concepts and new developments. Kluwer, Dordrecht 1998, ISBN 978-0-7923-5146-7

Weblinks

• Die bunte Welt der Schwarzen Löcher auf Werner Kaspers Website Abenteuer Universum (ausführlich, aber leicht verständlich)
• The Nature of Space and Time – Part 1–4, Vorlesungen von Stephen Hawking als PostScript oder PDF (Teil 2 enthält eine schöne Karikatur des No-Hair-Theorems)

Videos

Alle folgenden Flash Videos sind aus der Fernsehsendung alpha-Centauri:

• Was sind Schwarze Löcher? 3. Januar 1999
• Gibt es Schwarze Löcher in der Milchstraße? 9. Mai 1999
• Wo ist das nächste Schwarze Loch? 4. Juni 2000
• Verschmelzen Schwarze Löcher? 27. Mai 2001
• Bewegen sich Schwarze Löcher im All? 20. Januar 2002
• Tanzen Schwarze Löcher? 21. Januar 2004
• Fressen Schwarze Löcher Sterne? 27. Oktober 2004
• Rotieren Schwarze Löcher? 16. Februar 2005
• Gibt es ein 2. Schwarzes Loch im Galaktischen Zentrum? 10. Mai 2006

Fußnoten

1. ↑ Detaillierter Übersichtsartikel von Andreas Müller
2. ↑ R. Genzel et al.: Near-IR Flares from accrediting gas near the last stable orbit around the supermassive Black Hole in the Galactic Centr.; Nature, 425, 934 (2003)
3. ↑ NASA Bericht
4. ↑ M. W. Pakull u. a.: Ultraluminous X-Ray Sources: Bubbles and Optical Counterparts. Preprint auf http://arXiv.org/abs/astro-ph/0603771
5. ↑ Xiaobo Dong et al.: SDSS J160531.84+174826.1: A Dwarf Disk Galaxy With An Intermediate-Mass Black Hole. Preprint auf http://arXiv.org/abs/astro-ph/0610145
6. ↑ Sterne und Weltraum, Mai 2008, S.21, Ein Schwarzes Loch in Omega Centauri
7. ↑ wissenschaft.de: Ein Monster im Visier, Astronomen vermessen das Schwarze Loch im Milchstraßenzentrum, Nachricht vom 10. Dezember 2008
8. ↑ Natarajan und Treister: Is there an upper limit to black hole masses? http://arxiv.org/PS_cache/arxiv/pdf/0808/0808.2813v2.pdf, 2008
9. ↑ J. Casares: Observational evidence for stellar mass black holes. Preprint
10. ↑ M. R. Garcia et al.: Resolved Jets and Long Period Black Hole Novae. Preprint
11. ↑ wissenschaft.de: Das kleine Schwarze
12. ↑ A. P. Cowley et al. (1983), Astroph. Journ. 272, 118 [1]