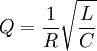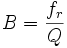Schwingquartz

Schwingquarz (Dickenschwinger, ca. 4 MHz), rechts Gehäuse entfernt.

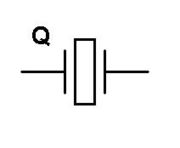
Ein Schwingquarz (engl.: crystal), manchmal abgekürzt auch als Quarz oder englisch quartz bezeichnet, ist ein aus einem piezoelektrischen Quarzkristall herausgeschnittenes Plättchen, das beidseitig metallisiert und kontaktiert und, nur durch die Anschlüsse gehalten, frei in einem luftdichten Gehäuse montiert ist.

Der Schwingquarz führt im elektrischen Wechselfeld Deformationsschwingungen (Longitudinal-, Torsions- oder Biegeschwingungen) aus, wenn die Frequenz des Wechselfeldes mit der Eigenfrequenz des Quarzplättchens übereinstimmt. So wirkt der Schwingquarz wie ein elektrischer Resonanzkreis mit sehr geringer Dämpfung (= sehr hohem Gütefaktor).

Schwingquarz für 100 kHz, Sowjetunion ca. 1970

Elektrisches Schaltzeichen eines Schwingquarzes

Ein Quarz kann in Serien- oder Parallelresonanz betrieben werden. Die beiden Eigenfrequenzen liegen sehr eng beieinander. Die Resonanzfrequenz lässt sich geringfügig auch durch die äußere Beschaltung beeinflussen. Häufig wird dazu ein Trimmer mit wenigen pF in Serie zum Quarz geschaltet, um Herstellungstoleranzen ausgleichen zu können ("ziehen" des Quarzes). Die elektrische Schaltung dieser speziellen Oszillatoren nennt sich Quarzoszillator.

Die Eigenfrequenzen des Quarzes sind in geringem Maße von der Temperatur abhängig. Der Temperaturkoeffizient lässt sich jedoch durch Wahl des Quarzschnitts (Geometrie in Bezug auf die Kristallachsen) beeinflussen, so dass er für die Verwendung als Zeitbasis sehr gering gehalten werden kann. Um Frequenzänderungen besonders gering zu halten, kann der Schwingquarz auch durch einen Quarzofen thermostatiert werden.

Anwendungen

Schwingquarze finden hauptsächlich Anwendung in der Elektrotechnik und Nachrichtentechnik; überall dort, wo eine konstante Frequenz oder eine genaue Zeitbasis gebraucht wird. Sie finden sich z. B. in praktisch allen Sendeanlagen, seltener in Empfängern, in Quarzuhren, als Taktgeber in Computern und Mikrocontrollern sowie in Frequenzzählern und digitalen Signalgeneratoren. Ebenso eignen sich Quarze zur Realisierung von Filtern.

Mit entsprechend geschnittenen Quarzen sind durch den Temperaturgang der Resonanzfrequenz sehr genaue Temperatursensoren herstellbar.

In Beschichtungsanlagen dienen frei aufgehängte Schwingquarze der Messung der erreichten Schichtdicke, indem die Änderung ihrer Resonanzfrequenz verfolgt wird, die durch die Massenzunahme infolge der auf dem Quarz entstehenden Schicht entsteht.

Elektrische Ersatzschaltung

Elektrische Ersatzschaltung

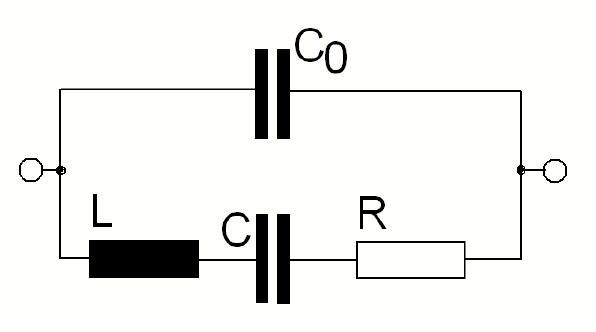
Elektrisch verhält sich ein Schwingquarz in einer Oszillatorschaltung wie ein Serienresonanzkreis bestehend aus einer Induktivität L und Kapazität C. Da ein Schwingquarz ein mechanisches System ist, treten in der Ersatzschaltung neben der statischen Kapazität C₀, verursacht durch die elektrischen Anschlüsse am Quarz, auch die durch das mechanische System gebildete dynamische Kapazität C, die durch die schwingende Masse verursachte Induktivität L und die mechanischen Schwingungsverluste (Reibung), dargestellt durch den ohmschen Widerstand R, auf. Für hohe Frequenzen muss das elektrische Ersatzschema noch durch einen Serienwiderstand für die ohmschen Verluste und einer kleinen Serieninduktivität für die elektrischen Anschlussleitungen erweitert werden.

Typisch sind dabei sehr große Werte für die Induktivität L und sehr kleine Werte für die Kapazität C, welche beide das mechanische System elektrisch abbilden. Beispielsweise liegen die Werte bei einem handelsüblichen Schwingquarz mit 10 MHz bei L = 25 mH und C = 0,01 pF. Die mechanischen Verluste bewegen sich im elektrischen Ersatzschaltbild im Bereich von R = 65 Ω, die statische Anschlusskapazität C₀ im Bereich von 5 pF.

Aufgrund der Beziehung für die Güte Q eines Resonanzkreises

$Q=\frac{1}{R} \sqrt{\frac{L}{C}}$

ergibt sich wegen des großen Werts für L und des sehr kleinen Werts für C eine sehr hohe Güte Q. Die Güte liegt dabei im Bereich von 25000 und mehr. Die Bandbreite B einer Resonanzschaltung wird direkt durch die Beziehung

$B=\frac{f_r}{Q}$

ausgedrückt. Bei einem Quarz mit f_r = 10  MHz liegt somit die Bandbreite im Bereich von 400 Hz, was die hohe Frequenzgenauigkeit von Schwingquarzen erklärt.

Weblinks

• Das große Quarzkochbuch
• Das Quarzglossar
• Marvin E. Frerking, Fifty Years of Progress in Quartz Crystal Frequency Standards (1996, engl.)
• Warren A. Marrison, The Evolution of the Quartz Crystal Clock (1948, engl.)