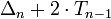Sechseckige Pyramidalzahl

In der Mathematik sind Pyramidenzahlen oder Pyramidalzahlen eine Klasse von Polyederzahlen, das heißt dreidimensionale figurierte Zahlen. Von manchen Autoren wird der Begriff Pyramidalzahl für den Spezialfall der quadratischen Pyramidalzahlen verwendet. Sie sind die dreidimensionalen Verallgemeinerungen der ebenen Polygonalzahlen.

Berechnung

Die jeweils n-te k-eckige Pyramidalzahl lässt sich mit der Formel

$\frac {n(n+1)[(k-2)n-k+5]} {6}$

berechnen.^[1]

Alternativ lässt sich die n-te k-eckige Pyramidalzahl als Summe der ersten n k-eckigen Polygonalzahlen berechnen.

Pyramidenzahlen zu Polygonen mit wenigen Ecken

k	Bezeichnung	Explizite Formel	die ersten Werte	Erzeugende Funktion
3	Tetraederzahlen	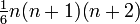$\tfrac 1 6 n(n+1)(n+2)$	(0,) 1, 4, 10, 20, 35, … (Folge A000292 in OEIS)	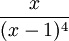$\frac x {(x-1)^4}$
4	Quadratische Pyramidalzahlen	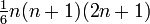$\tfrac 1 6 n(n+1)(2n+1)$	(0,) 1, 5, 14, 30, 55, … (Folge A000330 in OEIS)	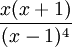$\frac {x(x+1)} {(x-1)^4}$ [2]
5	Fünfeckige Pyramidalzahlen	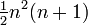$\tfrac 1 2 n^2(n+1)$	(0,) 1, 6, 18, 40, 75, … (Folge A002411 in OEIS)	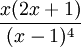$\frac {x(2x+1)} {(x-1)^4}$ [3]
6	Sechseckige Pyramidalzahlen	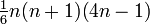$\tfrac 1 6 n(n+1)(4n-1)$	(0,) 1, 7, 22, 50, 95, … (Folge A002412 in OEIS)	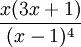$\frac {x(3x+1)} {(x-1)^4}$ [4]
7	Siebeneckige Pyramidalzahlen	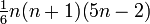$\tfrac 1 6 n(n+1)(5n-2)$	(0,) 1, 8, 26, 60, 115, … (Folge A002413 in OEIS)	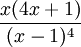$\frac {x(4x+1)} {(x-1)^4}$ [5]

Anmerkung: Manche Autoren zählen die Null als nullte oder erste figurierte Zahl jeweils dazu, andere nicht.

Weitere Zusammenhänge mit anderen figurierten Zahlen

Die n-te quadratische Pyramidalzahl lässt sich auch aus der n-ten Dreieckszahl Δ_n und der (n − 1)-ten Tetraederzahl T_{n − 1} nach der Formel

$\Delta_n + 2 \cdot T_{n-1}$

berechnen.

Außerdem sind die quadratische Pyramidalzahlen die Summe zweier aufeinanderfolgender Tetraederzahlen.

Die Summe der ersten Tetraederzahlen ergibt eine Pentatopzahl, eine vierdimensionale Figurierte Zahl.

Einzelnachweise

1. ↑ Eric W. Weisstein: Pyramidal Numbers auf MathWorld (englisch)
2. ↑ Eric W. Weisstein: Square Pyramidal Numbers auf MathWorld (englisch)
3. ↑ Eric W. Weisstein: Pentagonal Pyramidal Numbers auf MathWorld (englisch)
4. ↑ Eric W. Weisstein: Hexagonal Pyramidal Numbers auf MathWorld (englisch)
5. ↑ Eric W. Weisstein: Heptagonal Pyramidal Numbers auf MathWorld (englisch)