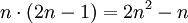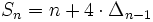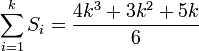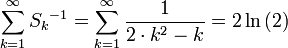Sechseckzahl

Ineinandergeschachtelte Sechsecke aus 28 Kugeln.

Eine Sechseckszahlen oder Hexagonalzahlen ist eine Zahl, die anhand der Formel

$n \cdot (2n - 1) = 2n^2 - n$

aus einer natürlichen Zahl n berechnet werden kann. Die ersten Sechseckszahlen sind

0, 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, … (Folge A000384 in OEIS)

Bei einige Autoren ist die Null keine Sechseckszahl, sodass die Zahlenfolge erst mit der Eins beginnt.

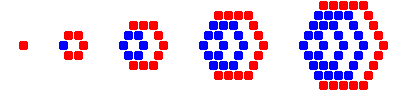
Der Name Sechseckszahl leitet sich von der geometrischen Figur des Sechsecks ab. Sechseckszahlen lassen sich als ineinandergeschachtelte Sechsecke mit steigender Kantenlänge legen. Sie zählen mit den Dreieckszahlen und Quadratzahlen zur Klasse der Polygonalzahlen. Bildet man die Sechsecke um ein gemeinsames Zentrum, dann erhält man die Hexzahlen (auch zentrierte Sechseckszahlen genannt).

Definition und Berechnung

Sechseckszahlen lassen sich als Sechseck auslegen, wie folgende Abbildung zeigt:

Die n-te Sechseckszahl bezeichnet man teilweise mit S_n. Sie lässt sich auch mit Hilfe der (n − 1)-ten Dreieckszahl Δ_{n − 1} berechnen.

$S_{n} = n + 4 \cdot \Delta_{n-1}$

Summen von Sechseckszahlen

Jede Zahl lässt sich nach dem fermatschen Polygonalzahlensatz als Summe von sechs Sechseckszahlen darstellen. Adrien-Marie Legendre bewies 1830, dass jede Zahl, die größer als 1792 ist, sogar als Summe von nur vier Sechseckszahlen geschrieben werden kann.^[1] Unter den kleineren Zahlen gibt es 13 Zahlen, die nicht Summe vierer Sechseckszahlen sind:

5, 10, 11, 20, 25, 26, 38, 39, 54, 65, 70, 114, 130 (Folge A007527 in OEIS).

Davon sind 11 und 26 die einzigen Zahlen, die nicht als Summe von fünf Sechseckszahlen dargestellt werden können.^[2]

Die Summe der ersten k Sechseckszahlen ist

$\sum_{i=1}^{k} S_{i} = \frac{4k^3+3k^2+5k}{6}$

die k-te sechseckige Pyramidalzahl

Reihe der Kehrwerte

Die Summe der Kehrwerte aller Sechseckszahlen ist

$\sum_{k=1}^{\infty} {S_k}^{-1} = \sum_{k=1}^{\infty} \frac{1}{2 \cdot k^2 - k} = 2 \ln{(2)}$

Einzelnachweise

1. ↑ Leonard Eugene Dickson: History of the Theory of Numbers. Volume II: Diophantine Analysis. Dover Publications, ISBN 0-486-44233-0, S. 18
2. ↑ Eric W. Weisstein: Hexagonal Number auf MathWorld (englisch)