Sehnensatz

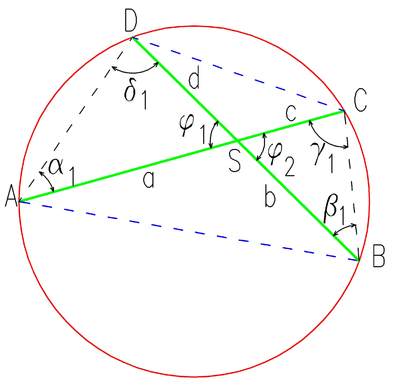
Der Sehnensatz besagt: Schneiden zwei Sehnen einander in einem Punkt S, so ist das Produkt der jeweiligen Sehnenabschnitte gleich.

Gegeben sei ein Kreis mit zwei Sehnen die sich in einem Punkt S schneiden. Bezeichnet man die Schnittpunkte des Kreises mit der einen Sehne als A beziehungsweise C und die der anderen Sehne mit B beziehungsweise D, so entsteht ein Sehnenviereck und es gilt:

$\overline{AS} \cdot \overline{CS} = \overline{BS} \cdot \overline{DS} \Rightarrow a \cdot c = b \cdot d$

Diese Aussage kann man auch als Verhältnisgleichung formulieren:

$\overline{AS} : \overline{DS} = \overline{BS} : \overline{CS} \Rightarrow {a \over d}={b \over c}$

Umgekehrt gilt auch: Wenn für die Diagonalen eines Vierecks ABCD mit dem Diagonalenschnittpunkt S gilt:

$\overline {AS} \cdot \overline {CS} = \overline {BS} \cdot \overline {DS} \Rightarrow a \cdot c = b \cdot d$

dann besitzt dieses Viereck einen Umkreis.

Literatur

• Max Koecher, Aloys Krieg: Ebene Geometrie. 2. neu bearbeitete und erweiterte Auflage. Springer-Verlag, Berlin u. a. 2000, ISBN 3-540-67643-0 (Springer-Lehrbuch).
• Hans Schupp: Elementargeometrie. Schöningh, Paderborn 1977, ISBN 3-506-99189-2, S. 149 (Uni-Taschenbücher 669).

Weblinks

 Wikibooks: Beweis des Sehnensatzes – Lern- und Lehrmaterialien