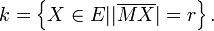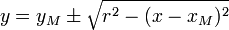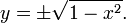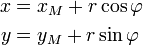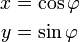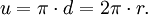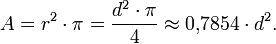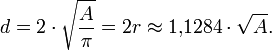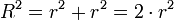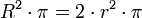Kreisformel

M = Mittelpunkt; r = Radius; d = Durchmesser

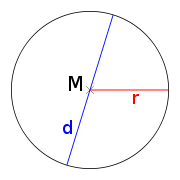
Der Begriff Kreis gehört zu den wichtigsten Begriffen der ebenen Geometrie. Ein Kreis ist definiert als Menge (geometrischer Ort) aller Punkte der euklidischen Ebene, deren Abstand von einem vorgegebenen Punkt M gleich einer festen positiven reellen Zahl r ist. Diese Definition entspricht dem Zeichnen eines Kreises mit dem Zirkel.

Definitionen

Formal ausgedrückt lautet die Definition für einen Kreis k in der Ebene E

$k = \left\{X \in E \vert |\overline{MX}| = r \right\}.$

Der konstante Abstand r wird als Radius des Kreises bezeichnet, der Punkt M als Mittelpunkt. Der doppelte Radius heißt Durchmesser und wird zumeist durch die Variable d ausgedrückt.

Nach der gegebenen Definition ist ein Kreis eine Kurve, also ein eindimensionales Gebilde, und keine zweidimensionale Fläche. Da das Wort „Kreis“ aber oft ungenau für die eingeschlossene Fläche benutzt wird, verwendet man zur Verdeutlichung häufig die Begriffe Kreislinie oder Kreisrand anstatt Kreis – im Gegensatz zur Kreisfläche oder (geschlossenen) Kreisscheibe. Diese ist definiert als die Menge aller Punkte der Ebene, deren Abstand von M höchstens r ist. Das Innere dieser Fläche bezeichnet man als offene Kreisscheibe. Ihre Punkte haben von M einen Abstand kleiner als r.

Nach einer anderen, äquivalenten, Definition ist ein Kreis die Menge aller Punkte in der Ebene, für die der Quotient q ihrer Abstände von zwei gegebenen Punkten konstant ist. Die beiden Punkte liegen auf einem von M ausgehenden Strahl im Abstand r / q bzw. r * q und wechselseitig auf der Polaren des jeweils anderen Punktes als Pol. Ähnliche Definitionen gibt es auch für die Ellipse (konstante Summe), Hyperbel (konstante Differenz) und die Cassinische Kurve (konstantes Produkt der Abstände).

Grundlegende Eigenschaften

• Alle Kreise sind zueinander ähnlich, das heißt, durch die Angabe einer einzigen Größe (zum Beispiel des Durchmessers) ist ein Kreis – bis auf Kongruenz – eindeutig bestimmt. In diesem Sinne ist es also gerechtfertigt, von dem Kreis zu sprechen.

• Der Kreis ist eine Figur von maximaler Symmetrie. Jeder Durchmesser ist eine Symmetrieachse. Jede Drehung um den Mittelpunkt bildet den Kreis auf sich selbst ab. Er ist damit – neben der Geraden – die einzige ebene Figur mit unendlich vielen Kongruenzabbildungen auf sich selbst.

• Der Kreis ist – wiederum neben der Geraden – die einzige ebene Kurve mit konstanter Krümmung. Seine Krümmung ist überall k = 1 / r.

• Der Kreis ist unter allen geschlossenen Kurven gleicher Länge diejenige mit dem größten Flächeninhalt (isoperimetrische Eigenschaft des Kreises).

Gleichungen

Koordinatengleichung

In der analytischen Geometrie werden geometrische Objekte meistens mit Hilfe eines kartesischen Koordinatensystems beschrieben. Der Kreis mit dem Mittelpunkt M(x_M | y_M) und dem Radius r lässt sich (in der Ebene) durch eine Koordinatengleichung

(x − x_M)² + (y − y_M)² = r²

ausdrücken.

Diese allgemeine Kreisgleichung ergibt sich unmittelbar aus der Kreisdefinition (siehe oben) und dem Satz des Pythagoras. x und y sind die Koordinaten eines beliebigen Punktes auf dem Kreis.

Ein wichtiger Spezialfall ist die Koordinatengleichung des Einheitskreises

x² + y² = 1.

Funktionsgleichung

Da der Kreis kein Funktionsgraph ist, lässt er sich auch nicht durch eine Funktionsgleichung darstellen. Behelfsweise kann ein Paar von Funktionsgleichungen

$y = y_M \pm \sqrt{r^2 - (x-x_M)^2}$

verwendet werden. Für den Einheitskreis vereinfacht sich dieses zu

$y = \pm \sqrt{1 - x^2}.$

Parameterdarstellung

Eine andere Möglichkeit einen Kreis durch Koordinaten zu beschreiben bietet die Parameterdarstellung (siehe auch Polarkoordinaten):

$\begin{align} x &= x_M + r\cos\varphi\\ y &= y_M + r\sin\varphi \end{align}$

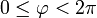Hier werden die Koordinaten x und y durch den Parameter $\varphi$ ausgedrückt, der alle Werte mit $0 \le \varphi < 2 \pi$ annehmen kann.

Wendet man auch diese Gleichungen speziell auf den Einheitskreis an, so erhält man:

$\begin{align} x &= \cos\varphi\\ y &= \sin\varphi \end{align}$

Kreisberechnung

Umfang des Kreises mit d = 1

Da alle Kreise ähnlich sind, ist das Verhältnis von Kreisumfang und Kreisdurchmesser für alle Kreise konstant. Der Zahlenwert dieses Verhältnisses definiert die Kreiszahl pi (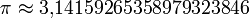$\pi \approx 3{,}14159265358979323846$). Es handelt sich hierbei um eine transzendente Zahl, bei der sich gezeigt hat, dass sie in vielen Bereichen der höheren Mathematik eine herausragende Bedeutung besitzt.

Umfang

Im Rahmen der Elementargeometrie ist π das Verhältnis von Kreisumfang zu dessen Durchmesser, und zwar für beliebige Kreise. Somit gilt

$u = \pi \cdot d = 2 \pi \cdot r.$

Kreisfläche

Der Flächeninhalt der Kreisfläche A (lat. area: Fläche) ist proportional zum Quadrat des Radius r bzw. des Durchmessers d des Kreises. Man bezeichnet ihn auch als Kreisinhalt.

Um die Formel für den Kreisinhalt zu erhalten, sind Grenzwert-Betrachtungen unerlässlich. Recht anschaulich ergibt sich eine solche aus der folgenden Zeichnung:

Die Kreisfläche ist zerlegungsgleich mit der Fläche der rechten Figur. Diese nähert sich – bei feiner werdender Segment-Einteilung – „offensichtlich“ einem Rechteck an mit der Länge 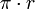$\pi \cdot r$ und der Breite r. Die Flächenformel ist somit

$A = r^2 \cdot \pi = \frac{d^2\cdot\pi}{4} \approx 0{,}7854 \cdot d^2.$

Die Flächenformel kann zum Beispiel durch Integrieren der Kreisgleichung oder mit Hilfe der unten beschriebenen Annäherung durch regelmäßige Vielecke bewiesen werden.

Durchmesser

Der Durchmesser ist

$d = 2 \cdot \sqrt{\frac A\pi} = 2r \approx 1{,}1284 \cdot \sqrt A.$

Formeln

siehe auch: Formelsammlung Geometrie

Formeln zum Kreis
Umfang	U = 2πr = πd
Flächeninhalt	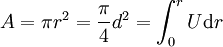$A = \pi r^2 = \frac{\pi}4 d^2 = \int_0^r U \mathrm dr$
Fläche eines Kreisringes	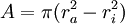$A = \pi (r_a^2-r_i^2)$
Länge eines Kreisbogens	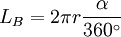$L_B = 2\pi r \frac{\alpha}{360^\circ}$
Fläche Kreissektor (in Grad)	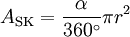$A_\mathrm{SK} = \frac{\alpha}{360^\circ} \pi r^2$
Fläche eines Kreissegments	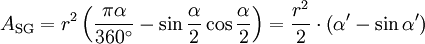$A_\mathrm{SG} = r^2 \left(\frac{\pi \alpha}{360^\circ} - \sin \frac{\alpha}2 \cos \frac{\alpha}2 \right)=\frac{r^2}2 \cdot \left(\alpha'-\sin\alpha'\right)$
Länge Kreissehne	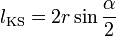$l_\mathrm{KS} = 2r \sin\frac \alpha 2$
Kreisradius	r
Öffnungswinkel in Grad, (bzw. Bogenmaß)	α, (α')
Höhe (Kreissegment)	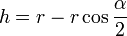$h = r-r \cos\frac \alpha 2$
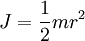
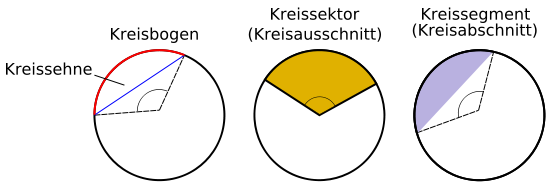
Trägheitsmoment (Kreisscheibe um Mittelpunkt)	$J = \frac 12 mr^2$

Kreisteile

Eine zusammenhängende Teilmenge des Kreises (also der Kreislinie) ist ein Kreisbogen. Eine Verbindungsstrecke zweier Punkte der Kreislinie bezeichnet man als Kreissehne. Die längsten Kreissehnen sind diejenigen, die durch den Mittelpunkt verlaufen, also die Durchmesser. Ein Kreissektor (Kreisausschnitt) ist eine Fläche, die von einem Kreisbogen und zwei Radien begrenzt wird. Bilden diese zwei Radien einen Durchmesser, so wird dieses auch als Halbkreis bezeichnet. Kreissegmente (Kreisabschnitte) werden von einem Kreisbogen und einer Kreissehne eingeschlossen.

Näherungsrechnungen

Die Näherungsrechnungen liefern zugleich eine Näherung für den Zahlenwert von π:

Auszählen in einem Raster

Die Fläche eines Kreises lässt sich annähernd bestimmen, indem man ihm kleine Quadrate unterlegt. Zählt man alle Quadrate, die vollständig innerhalb des Kreises liegen, so erhält man einen etwas zu niedrigen Wert für die Fläche, zählt man auch alle Quadrate mit, die den Kreis lediglich schneiden, so ist der Wert zu groß. Der Mittelwert beider Ergebnisse ergibt eine Näherung für den Flächeninhalt des Kreises, deren Güte mit der Feinheit des Quadrat-Rasters steigt.

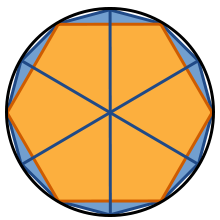
Annäherung durch Vielecke

Bei einer anderen Möglichkeit zur Kreisflächenbestimmung ist in den Kreis ein regelmäßiges Sechseck einzuzeichnen, dessen Ecken auf dem Kreis liegen. Werden nun die Seitenmitten vom Mittelpunkt aus auf den Kreis projiziert und diese neuen Punkte mit den alten Ecken verbunden, so entsteht ein regelmäßiges Zwölfeck. Wird dieser Vorgang wiederholt, entstehen nacheinander ein 24-Eck, ein 48-Eck und so fort.

Die Länge der Sechseck-Seite ist gleich dem Kreisradius. Die Seiten der folgenden Vielecke ergeben sich mit Hilfe des Satzes von Pythagoras jeweils aus den Seiten der vorhergehenden. Aus den Seiten lassen sich die Flächen der Vielecke durch Dreiecksflächenberechnung exakt bestimmen. Sie sind alle etwas kleiner als die Kreisfläche, der sie sich bei steigender Eckenzahl jedoch annähern.

Entsprechend kann man mit einem Sechseck verfahren, das von außen an den Kreis gezeichnet ist, dessen Seitenmitten also auf ihm liegen. Man erhält eine fallende Folge von Flächenmaßen, deren Grenzwert wiederum die Kreisfläche ist.

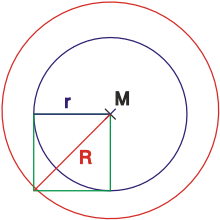
Flächenverdoppelung

Die Fläche eines Kreises lässt sich geometrisch verdoppeln, indem ein Quadrat gezeichnet wird, dessen eine Ecke im Kreismittelpunkt liegt, wobei zwei weitere Ecken auf dem Kreisbogen liegen. Durch die vierte Ecke wird ein Kreis um den alten Mittelpunkt gezogen. Dieses Verfahren wurde im 13. Jahrhundert im Bauhüttenbuch des Villard de Honnecourt dargestellt.

Dieses Verfahren funktioniert, da (nach dem Satz des Pythagoras)

$R^2=r^2+r^2=2\cdot r^2$

und damit der Flächeninhalt des großen Kreises

$R^2\cdot\pi=2\cdot r^2\cdot\pi$

genau doppelt so groß ist, wie der des kleinen Kreises.

Lagebeziehungen zwischen Kreis und Gerade

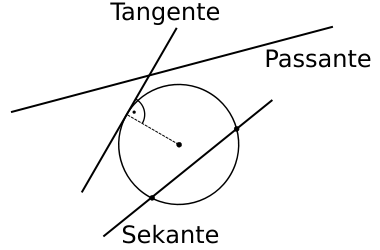
Für die Lage einer Geraden in Bezug auf einen gegebenen Kreis gibt es drei Möglichkeiten:

• Falls der Abstand des Kreismittelpunkts von der Geraden größer ist als der Kreisradius, dann haben Kreis und Gerade keinen Punkt gemeinsam. In diesem Fall bezeichnet man die Gerade als Passante.

• Stimmt der Abstand des Mittelpunkts zu der Geraden mit dem Radius überein, so gibt es genau einen gemeinsamen Punkt. Man sagt, dass die Gerade den Kreis berührt und nennt die Gerade eine Tangente. Eine Tangente steht im Berührpunkt senkrecht (orthogonal, normal) zum entsprechenden Radius.

• Ist der Abstand zwischen Mittelpunkt und Gerade kleiner als der Kreisradius, so haben Kreis und Gerade zwei (verschiedene) Schnittpunkte und man spricht dann von einer Sekante. Manchmal bezeichnet man den Spezialfall einer Sekante, die durch den Mittelpunkt eines Kreises verläuft als Zentrale.

Geometrische Sätze und Begriffe rund um den Kreis

Der Kreis ist achsensymmetrisch bezüglich jeder Geraden durch seinen Mittelpunkt und punktsymmetrisch bezüglich des Kreismittelpunkts. Die Symmetrieeigenschaften dürften der Grund dafür sein, dass der Kreis von jeher als besonders vollkommen empfunden wurde. Wegen dieser Vollkommenheit gingen die Astronomen lange Zeit fälschlicherweise davon aus, dass Planeten die Sonne auf Kreisbahnen umrunden, bis schließlich Johannes Kepler erkannte, dass die Planetenbahnen auf Ellipsen verlaufen.

Unter allen Flächen der euklidischen Ebene mit gegebenem Umfang besitzt die Kreisfläche den größten Flächeninhalt. Umgekehrt hat die Kreisfläche bei gegebenem Flächeninhalt den kleinsten Umfang.

Siehe hierzu auch:

• Thaleskreis
• Winkel am Kreis: Peripheriewinkel (Umfangswinkel), Zentriwinkel (Mittelpunktswinkel), Sehnentangentenwinkel
• Kreis des Apollonios
• Potenz, Sehnensatz, Sekantensatz, Sekanten-Tangenten-Satz

Das Winkelmaß Bogenmaß (Arcus) ist definiert als Verhältnis zwischen der Länge des Kreisbogens, den zwei Radien einschließen, die im angegebenen Winkel aufeinander stehen, und dem Radius. Die trigonometrischen Winkelfunktionen können im Einheitskreis (ein Kreis mit dem Radius 1) definiert werden.

Die Kreisebene ist die Ebene, auf der der Kreis aufliegt. Diesen Begriff benutzt man, um die Lage eines Kreises im Raum zu beschreiben.

Verallgemeinerungen

In der ebenen Geometrie kann der Kreis als spezielle Ellipse und damit als Kegelschnitt aufgefasst werden, bei dem die beiden Brennpunkte mit dem Kreismittelpunkt zusammenfallen. Beide Halbachsen sind dabei gleich dem Kreisradius.

Ebenso kann man Kreis und Gerade in der Ebene als Kurven zusammenfassen, die in einem Punkt eine bestimmte Richtung haben und überall eine konstante Krümmung aufweisen. Die Krümmung entspricht dabei dem Kehrwert des Radius. Die Ebene, in der diese Kurven liegen, kann dabei durchaus Teil eines höherdimensionalen Raums sein. Siehe auch Inversion.

Werden höhere Dimensionen in Betracht gezogen, so ist der Kreis ein Spezialfall einer Sphäre, nämlich eine 1-Sphäre.

Siehe auch

• Einheitskreis
• Kreisteilung, Quadratur des Kreises
• Apollonisches Problem
• Kurve (Mathematik)
• Kugel
• Zindlerkurve

Weblinks

• „Mathematische Basteleien“ zum Kreis