Semi-Thue System

Semi-Thue-System (oder auch Umformungssystem) ist in der Theoretischen Informatik ein Regelsystem zur Manipulation von Zeichenketten, also eine formale Grammatik.

Motiviert durch David Hilberts Vortrag im Jahre 1900 und den Ausführungen über eine logische Fundamentierung der Mathematik untersuchte der norwegische Mathematiker Axel Thue die Möglichkeiten, die reine Ableitungskalküle eröffnen, zunächst ganz grundlegend. Aus diesen Untersuchungen hat sich der heutige Begriff des Thue-Systems und des Semi-Thue-Systems herausgebildet.

Die auch in der Logik häufig verwendeten Ableitungs-Kalküle stammen von Emil Leon Post (1936) und als Ersetzungssysteme für Zeichenketten schließlich schon 1914 von Axel Thue. Die Thue-Systeme bilden den Ausgangspunkt zur Definition von Chomsky-Grammatiken, denn sie erweitern den Gedanken der Symbolersetzung auf ganze Zeichenketten.

Definition

Ein Semi-Thue System (STS) über einem Alphabet Σ ist eine (endliche oder unendliche) Teilmenge 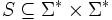$S \subseteq \Sigma^* \times \Sigma^*$, notiert meist als S anstelle des korrekten Tupels (Σ,S). Die Elemente 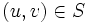$(u,v)\in S$ nennt man Produktionen oder Ableitungsregeln und schreibt diese meistens als 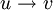$u \rightarrow v$. Die zu S gehörende einschrittige Ableitungsrelation "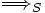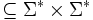$\Longrightarrow_S$" $\subseteq \Sigma^* \times \Sigma^*$ wird so definiert:

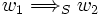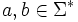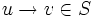• $w_1\Longrightarrow_S w_2$, wenn w₁ = aub und w₂ = avb für $a,b\in \Sigma^*$ sowie $u\rightarrow v\in S$ gilt.

Die reflexiv-transitive Hülle von 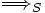$\Longrightarrow_S$ wird mit 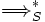$\Longrightarrow_S^*$ bezeichnet und ist die von S definierte Ableitungsrelation. Auf der Basis von 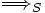$\Longrightarrow_S$ werden für $n\in \mathbb{N}$ die Relationen "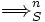$\Longrightarrow_S^n$" erklärt:

• $\Longrightarrow_S^n \,\,\,\,:= \,\,\,\,\Longrightarrow_S^{n-1}\circ \Longrightarrow_S$,

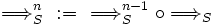wobei

• $\Longrightarrow_S^0 \,\,\,\,:= \,\,\,\,Id_S$

Dies beschreibt die Ableitungen in genau n Schritten.

Der Index S kann weggelassen werden, wenn S aus dem Zusammenhang eindeutig ist.

Thue-System

Wenn das Semi-Thue-System symmetrisch ist, d.h. mit 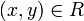$(x,y)\in R$ ist stets auch 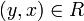$(y,x)\in R$, dann heißt das System auch Thue-System. Jede Regel ist somit beidseitig anwendbar.

Die Frage, ob mit einem Semi-Thue-System (Σ,S) ein Wort u in ein Wort v umgeformt werden kann, heißt das Wortproblem des Systems (Σ,R).