Semi-entscheidbar

Als semi-entscheidbare Menge (auch halb-entscheidbare Menge) wird in der Berechenbarkeitstheorie eine Menge A bezüglich einer Grundmenge M bezeichnet, wenn ihre partielle charakteristische Funktion 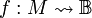$f:M\rightsquigarrow \mathbb B$ definiert durch

$f(x) = \begin{cases}\top, & \mbox{falls } x\in A,\\ \mbox{undefiniert}, & \mbox{sonst,}\end{cases}$

berechenbar ist. Die Menge M muss dazu gödelisierbar sein. In der Theorie setzt man zum einfacheren Vergleich direkt 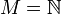$M=\mathbb{N}$ oder M = {0,1} ^* voraus. Im letzteren Fall hat man die Menge als das Wortproblem einer formalen Sprache dargestellt.

Hintergrund: Wenn eine Ausgabe 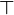$\top$ geliefert wird, ist eine positive Antwort eingetroffen; wenn diese Ausgabe nicht gekommen ist, muss man noch warten oder sie kommt nie. Es gibt semi-entscheidbare Mengen, deren Komplement nicht semi-entscheidbar ist.

Berechenbare Mengen

In der Literatur taucht gelegentlich der Begriff der berechenbaren Menge auf. Dieser Begriff wird uneinheitlich verwendet. Es können damit entscheidbare Mengen oder semi-entscheidbare Mengen gemeint sein.

Eigenschaften

• Eine Menge ist genau dann semi-entscheidbar, wenn sie rekursiv aufzählbar ist.
• Eine Menge ist genau dann semi-entscheidbar, wenn sie der Wertebereich einer berechenbaren Funktion ist.
• Eine formale Sprache ist genau dann semi-entscheidbar, wenn sie Typ-0 ist.
• Eine Menge ist genau dann entscheidbar, wenn sie und ihr Komplement semi-entscheidbar sind.

Beispiele

1. Das Halteproblem der Turingmaschinen ist semi-entscheidbar, denn man kann die gegebene Turingmaschine mit der gegebenen Eingabe laufen lassen und nach seiner Terminierung 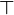$\top$ ausgeben. Das Komplement des Halteproblems ist nicht semi-entscheidbar.
2. Das Äquivalenzproblem der Turingmaschinen ist nicht semi-entscheidbar. Auch das Komplement des Äquivalenzproblems ist nicht semi-entscheidbar.

Siehe auch

• Entscheidbar