Semiperfekt

Ein semiperfekter Ring im mathematischen Teilgebiet der Algebra ist ein Ring, über dem jeder endlich erzeugte Linksmodul eine projektive Decke hat. Der Begriff wurde 1959/60 von Hyman Bass eingeführt.

Definition

Im folgenden sei R ein Ring mit 1, J=J(R) das Jacobson-Radikal.

Ein Ring R heißt semiperfekt, wenn er eine der folgenden äquivalenten Eigenschaften besitzt:

• Jeder einfache R-Links-/Rechtsmodul hat eine projektive Decke.
• Jeder endlich erzeugte R-Links-/Rechtsmodul hat eine projektive Decke.
• R/J ist halbeinfach, und jedes Idempotent von R/J lässt sich zu R heben.
• Es existiert eine Zerlegung 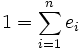$1 = \sum_{i=1}^ne_i$ mit paarweise orthogonalen, lokalen Idempotenten e₁,...,e_n

Eigenschaften

• Alle linksartinschen und alle rechtsartinschen Ringe sind semiperfekt.
• Jeder lokale Ring ist semiperfekt.
• Ein kommutativer Ring R ist genau dann semiperfekt, wenn R eine endliche direkte Summe von lokalen Ringen ist
• Ist R semiperfekt und I ein Ideal von R, dann ist auch der Faktorring R/I semiperfekt.
• Ist R semiperfekt und 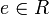$e \in R$ ein Idempotent, dann ist auch eRe semiperfekt.