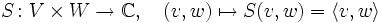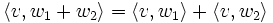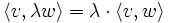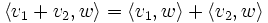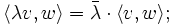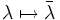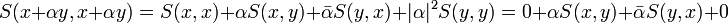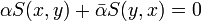Sesquilinear

Als Sesquilinearform (lat. sesqui = anderthalb) bezeichnet man in der linearen Algebra eine Funktion, die zwei Vektoren einen Skalarwert zuordnet, und die linear in einem, semilinear im anderen ihrer beiden Argumente ist.

Die beiden Argumente können verschiedenen Vektorräumen V,W entstammen, denen jedoch ein gemeinsamer Skalarkörper K zugrundeliegen muss; eine Sesquilinearform ist eine Abbildung 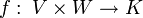$f:\;V\times W\to K$; sie ist eine Linearform bezüglich dem einen und eine Semilinearform bezüglich dem anderen Argument. Für die Reihenfolge von linearem und semilinearem Argument gibt es unterschiedliche Konventionen; in der Physik ist es üblich, das semilineare Argument zuerst zu nennen.

Relevant ist der Begriff Sesquilinearform nur über dem Körper der komplexen Zahlen $\mathbb C$; über den reellen Zahlen ist jede Sesquilinearform eine Bilinearform.

Definition

Es seien V,W Vektorräume über den komplexen Zahlen.

Eine Abbildung

$S\colon V\times W\to\mathbb C,\quad (v,w)\mapsto S(v,w)=\langle v,w\rangle$

heißt Sesquilinearform, wenn S semilinear im ersten und linear im zweiten Argument ist, d. h.

• $\langle v,w_1+w_2\rangle=\langle v,w_1\rangle+\langle v,w_2\rangle$
• $\langle v,\lambda w\rangle=\lambda\cdot\langle v,w\rangle$

und

• $\langle v_1+v_2,w\rangle=\langle v_1,w\rangle+\langle v_2,w\rangle$
• $\langle \lambda v, w\rangle=\bar\lambda\cdot \langle v,w\rangle;$

dabei sind 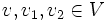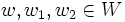$v,v_1,v_2\in V$, $w,w_1,w_2\in W$ und $\lambda\in\mathbb C$.

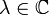Manchmal wird stattdessen auch Linearität im ersten und Semilinearität im zweiten Argument gefordert; dieser Unterschied ist jedoch rein formaler Natur.

Diese Definition lässt sich auch auf Vektorräume über anderen Körpern oder Moduln über einem Ring verallgemeinern, sobald auf dem Grundkörper bzw. -ring ein ausgezeichneter Automorphismus oder zumindest Endomorphismus

$\lambda\mapsto\bar\lambda$

gegeben ist. Ein Kandidat für derartige Endomorphismen ist der Frobeniushomomorphismus in positiver Charakteristik.

Die konstante Nullabbildung ist eine Sesquilinearform, wir schreiben S = 0. Punktweise Summen und skalare Vielfache von Sesquilinearformen sind wieder Sesquilinearformen. Die Menge der Sesquilinearformen bildet also einen $\mathbb{C}$-Vektorraum.

Beispiele

Das innere Produkt über einem komplexen Vektorraum ist eine Sesquilinearform mit Hermitescher Symmetrie, also sogar eine Hermitesche Form, siehe auch Kreinraum.

Eindeutige Bestimmtheit durch die Diagonale

Die Definition der Sesquilinearform mag zunächst komplizierter erscheinen als die der Bilinearform. Einer der Vorteile von Sequilinearformen ist jedoch die folgende Eigenschaft:

Ist S(x,x) = 0 für alle 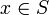$x \in S$, dann ist S = 0.

Folgerung: Ist S(x,x) = T(x,x) für alle x, dann (S − T)(x,x) = 0, also S = T.

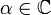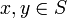Beweis: Erfülle S die Voraussetzung. Für $\alpha \in \mathbb{C}$ und $x,y \in S$ gilt nach Voraussetzung einerseits:

S(x + αy,x + αy) = 0

und andererseits durch Ausmultiplizieren:

$S(x + \alpha y, x+ \alpha y) = S(x,x) + \alpha S(x,y) + \bar{\alpha} S(y,x) + |\alpha|^2 S(y,y) = 0+\alpha S(x,y) + \bar{\alpha} S(y,x)+0$

also

$\alpha S(x,y) + \bar{\alpha} S(y,x) = 0$

für α = 1 erhalten wir:

S(x,y) + S(y,x) = 0

und für α = i und durch Kürzen von i:

S(x,y) − S(y,x) = 0

durch Addieren folgt S(x,y) = 0.

Für Bilinearformen ist die Behauptung falsch: Sei 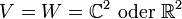$V=W=\mathbb{C}^2 \text{ oder } \mathbb{R}^2$. Setze

$S(x,y) := x^T \begin{pmatrix} 0&-1\\1&0 \end{pmatrix} y$.

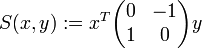Das ist offenbar bilinear und S(x,x) = − x₁x₂ + x₁x₂ = 0, aber S((1,0),(0,1)) = 1.

Folgerung

Sei 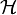$\mathcal{H}$ ein Hilbertraum, T ein (beschränkter) linearer Operator. Dann ist 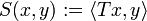$S(x,y):=\langle Tx, y \rangle$ eine (beschränkte) Sesquilinearform (und jede beschränkte Sesquilinearform lässt sich so schreiben). Nun ist S = 0 genau dann wenn T = 0 ($S=0 \implies \|Tx\|^2 = S(x,Tx)=0 \forall x \implies Tx = 0 \forall x$).

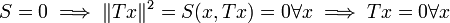Es folgt also, dass ein Operator Null ist, genau dann wenn 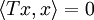$\langle Tx,x \rangle = 0$ für alle x.