Short (Datentyp)

Mit Integer (ˈɪntɪdʒə, englisch für ganze Zahl) wird in der Informatik ein Datentyp bezeichnet, der ganzzahlige Werte speichert. Der Wertebereich ist endlich. Berechnungen mit Integern sind in der Regel exakt. Lediglich ein Überlauf kann durch Überschreiten des zulässigen Wertebereichs auftreten. Als grundlegender arithmetischer Datentyp sind Integer in der Hardware fast aller Rechenanlagen vorhanden und in nahezu jeder Programmiersprache verfügbar. Meist werden sogar mehrere Integerarten bereitgestellt, die sich in der Darstellung, der Länge oder dem Vorhandensein eines Vorzeichens unterscheiden. Die implementierte Arithmetik mit Integern ist bisher nicht genormt und weist oft sprachabhängige (Java, C) oder sogar compilerabhängige (C – Reihenfolge der Auswertung von Ausdrücken) Eigenheiten auf. Ein Normungsversuch liegt mit der Language Independent Arithmetic vor.

Darstellungen von Integern

Von exotischen Darstellungen (Knuth, Vol 2, p. 195, 4.1 Positional number systems; p. 284, 4.3.2 Modular arithmetic) abgesehen gibt es drei Möglichkeiten zur Speicherung von Integern. Das Vorzeichen – soweit vorhanden – kann man in allen Darstellungen an einer bestimmten Ziffer ablesen.

In der Betrags-Vorzeichendarstellung werden das Vorzeichen und der Betrag getrennt gespeichert und verarbeitet.

Bei b-Komplementzahlen wird genau die halbe Teilmenge der Zahlen mit großem Betrag als negative Zahlen interpretiert, ohne dass die Arithmetik positiver Zahlen wesentlich geändert wird. Das führt zu einfachen Schaltungen und zu einer einfachen Regel für Vorzeichenänderungen (ziffernweises b-Komplement und anschließende Erhöhung der Zahl). Zwischen der Arithmetik mit Zweierkomplementzahlen und rein positiven Binärzahlen besteht kein Unterschied. Es existiert eine bijektive Abbildung zwischen den Darstellungen und den Werten (kein Wert hat zwei Darstellungen). Man kann b-Komplementzahlen wie technische Zähler (Kilometerzähler im Auto) interpretieren. Nachteil von b-Komplementzahlen ist der kleinste negative Wert, der kein positives Gegenstück in der Darstellung hat.

Bei (b − 1)-Komplementzahlen vereinfacht man dagegen die Regel für Vorzeichenänderungen (die anschließende Erhöhung fällt weg) und muss dafür in der Arithmetik mehr Fallunterscheidungen und vor allem zwei Darstellungen der Null (±0) berücksichtigen.

In modernen Rechenanlagen ist die Basis b praktisch ausnahmslos b = 2 und die Darstellung im Zweierkomplement hat sich weitgehend durchgesetzt.

Dezimale Äquivalente zum Zweier- und Einerkomplement im Binärsystem wären Zehner- und Neunerkomplementzahlen.

Von manchen Herstellern wird oft unter Berufung auf Kundenwünsche (Banken) noch ein Dezimalformat gepflegt. Hier wird fast ausnahmslos eine Betrags-Vorzeichendarstellung gewählt und der Betrag in der sogenannten BCD-Form (binary coded decimal) gespeichert.

Übersicht

	Zweierkomplement	Einerkomplement	Betrags-Vorzeichendarstellung	BCD-Zahlen
Basis	2	2	2	10
Eindeutigkeit	umkehrbar eindeutig	2 Darst. für denselben Wert (±0)	2 Darst. für denselben Wert (±0)	Darstellungen ohne Wert
Wertebereich	maximal, asymmetrisch	symmetrisch	symmetrisch	symmetrisch

Beispiele

(die Beispielzahlen sind für 9 Bit ausgelegt, da so zweistellige BCD-Zahlen möglich sind):

	Zweierkomplement	Einerkomplement	Betrags-Vorzeichendarstellung	BCD-Zahlen
Maximum	011111111 (255)	011111111 (255)	011111111 (255)	010011001 (99)
17	000010001	000010001	000010001	000010111
5	000000101	000000101	000000101	000000101
1	000000001	000000001	000000001	000000001
0	000000000	000000000	000000000	000000000
−0		111111111	100000000	100000000
−1	111111111	111111110	100000001	100000001
−2	111111110	111111101	100000010	100000010
−5	111111011	111111010	100000101	100000101
−17	111101111	111101110	100010001	100010111
Minimum+1	100000001 (−255)	100000001 (−254)	111111110 (−254)	110011000 (−98)
Minimum	100000000 (−256)	100000000 (−255)	111111111 (−255)	110011001 (−99)

Häufige Speicherformen

Eine Integer besteht in der Regel aus 8, 16, 32, 64 oder 128 Bits (also 1, 2, 4, 8 oder 16 Bytes) – entsprechend der Wortbreite der jeweiligen CPU. Historisch wurden auch andere Werte (12, 48, ... Bit) verwendet. In Programmiersprachen sind die Bezeichnungen dieser Zahlen teilweise genormt: In Java werden sie als byte (8), short (16), int (32) und long (64 Bit) bezeichnet. In C gibt es dieselben Bezeichnungen, ohne dass die Größe damit festgelegt wäre. Dafür existieren in C zusätzlich vorzeichenlose (unsigned) Varianten mit leicht anderen Arithmetikregeln.

Die Rechenanlagen verarbeiten Integer meist schneller als Gleitkommazahlen, da einerseits oft weniger Bits zu verarbeiten sind (kleinste IEEE-754-Gleitkommazahl hat 32 Bit) andererseits bei ganzen Zahlen die Verarbeitung des Exponenten entfällt, was natürlich Zeit einspart. Bei modernen Rechenanlagen werden diese Zeitverluste durch intensive Parallelverarbeitung, Cachetechniken und Pipelining weitgehend ausgeglichen.

Bei der Ablage im Speicher taucht neben der Notwendigkeit, die Bits der Zahlendarstellung überhaupt abzulegen, noch das Problem der Bytereihenfolge und Anordnung auf.

Maximaler Wertebereich von Integern

Größe (Bit)	Typische Namen	Vorzeichen	Grenzen des Wertebereichs (Zweierkomplement)		Dezimalstellen (ohne Vorzeichen)
			min	max
8	char, Byte, byte	signed	−128	127	3
		unsigned	0	255	3
16	Word, Short, Integer, short	signed	−32.768	32.767	5
		unsigned	0	65.535	5
32	DWord, Double Word, int	signed	−2.147.483.648	2.147.483.647	10
		unsigned	0	4.294.967.295	10
64	Int64, QWord, Quadword, Long, long	signed	−9.223.372.036.854.775.808	9.223.372.036.854.775.807	19
		unsigned	0	18.446.744.073.709.551.615	20
128	Int128, Octaword, Double Quadword	signed	≈ −1,70141·1038	≈ 1,70141·1038	39
		unsigned	0	≈ 3,40282·1038	39
n	BigInteger	signed	− 2n − 1	2n − 1 − 1	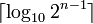$\lceil \log_{10}{2^{n-1}} \rceil$
		unsigned	0	2n − 1	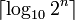$\lceil \log_{10}{2^n} \rceil$

Siehe auch

• Gleitkommazahl
• Digitale Auflösung

Literatur

• Donald E. Knuth: The Art of Computer Programming. 2. Seminumerical Algorithms. 3. Auflage, Addison-Wesley, Amsterdam 2001, ISBN 0-201-89684-2.